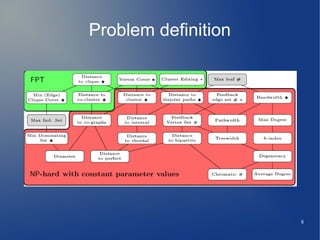
The document summarizes research on the parameterized complexity of the graph MOTIF problem. It begins by defining the problem and providing an example. It then discusses how graph MOTIF can be solved efficiently using different parameters, such as cluster editing, distance to clique, and vertex cover number. The document also analyzes parameters for which graph MOTIF remains NP-hard, such as the deletion set number parameter. In conclusion, it provides references for the algorithms and results discussed.

1. 1
Parametrized complexity of Graph
MOTIF
By: Amr Koura

2. 2
Agenda
● Problem definition
● Preliminaries
● FPT algorithms
● Parameters for which graph MOTIF is hard
● References

3. 3
Problem Definition

4. 4
Problem definition
● Input: A triple (G,c,M) where G=(V,E) is graph,
c:V-->C is coloration function of V on |C|
colors, and M is multiset of Colors of C.
● Output: A subset such that G(P) is
connected and c(P)=M.
P⊂V

5. 5
Example
M={red,blue,red,yellow,black,orange,green}

6. 6
Solution
M={red,blue,red,yellow,black,orange,green}

7. 7
Problem Definition
● The problem is NP-hard.
● Application: Biological,social and technical
Networks.

8. 8
Problem definition

9. 9
Preliminaries

10. 10
Some Definitions
•
For any vertex , the set of neighbors of V is
N(v) and for , ,
and .
•
Vertex v dominate S if ,set R dominate
S if .
•
Denote the multiplicity of x in multiset M,
and .
v∈V
S⊂V N (S)=∪
v∈S
N (v)∖ S
S⊆N (v)
S⊆N (R)
mM x
∣M∣= ∑
x∈M
mM x
N [v]=N (v)∪{v}
N [S ]=N (S)∪S

11. 11
Some Definitions
•
clique is a graph where each two distinct
vertices are connected.
•
cluster is a graph set of disjoint union of
cliques.
•
(I,K) is fixed parameter traceable “FPT” if it can
be solved in where f is computable
function and c is constant.
•
If C is graph class , distance of graph G to C is
number of vertices to be removed from G to get
C.
f (K).∣I∣
c

12. 12
FPT algorithms

13. 13
FPT Algorithm parameter
● Cluster editing.
● Distance to clique.
● Vertex cover number.

14. 14
Cluster editing
parameter

15. 15
Cluster editing
•
Definition:Definition: number of edge deletion or additionnumber of edge deletion or addition
requited to get cluster.requited to get cluster.
• Theorem: Graph MOTIF can be solved in
with cluster editing K.
• Proof:
use parameter “neighborhood diversity”.
O
∗
(8
k
)

16. 16
Neighborhood diversity
Definition:
● Graph G has neighborhood diversity K if its
vertices can be partitioned into at most K sets
such that all vertices in the set have the same
type.
● Two vertices u,v have the same type if N(u)
{v}=N(v){u}.

17. 17
Neighborhood diversity
http://www.sofsem.cz/sofsem12/files/presentations/Wednesday/SRF/Ganian.pdf

18. 18
Cluster editing
• Theorem: graph MOTIF can be solved in on graph with
neighborhood diversity K [1].
➢ Compute neighborhood diversity:
- G is input graph, G' graph obtained after k edition on G.
- let X is set of vertices that are endpoints of the edit edges.
- Then
- Let is L cliques of G'.
- ,so number of neighborhood
diversity of G is bounded by .
- applying the above theorem , Graph MOTIF can be solved in
O
∗
(2
k
)
∣x∣≤2k
C1,. .. ,C L
∀i∈[L]∀v∈Ci ∖ X , N [v]=Ci
∣x∣+ l≤2k+ k=3k
O∗
(23k
)=O∗
(8k
)

19. 19
Distance to Clique

20. 20
Distance to clique
• Theorem: graph MOTIF can be solved in
where k is distance of input graph to clique.
• Proof: Algorithm:
- Find vertex cover S of size k in in time [2].
- S is also the distance to clique in G.
- let R be solution, trying all subset of S, guess subset of
S, which is in R.
- ,then vertices of the clique C with colors
should complete the solution.
- Problem: finding a minimal (inclusion wise) set such
that and G[ ] is connected.
O
∗
(2
klogk
)
G 1.2738k
2k
S '=S∩R
c(S ')⊆M ∣M∣−∣S '∣
M '=M ∖c(S ')
R'⊆C
c(R')⊆M ' R'∪S '

21. 21
Distance to clique
• Proof: Algorithm “continue”:
- Let be connected components of G[S'],
- build graph G'=(V',E') from graph G:
+Keep the clique C as it is.
+ contract into single vertex and draw
and edge from to iff and
+ a minimal (inclusion wise) in a dominating
vertex in G',
+ try out all l-partitions of denoted by
st: dominate . note that .
+ number of partitions : “Bell number”.
C1, C2,. .. ,Ck ' k '< k
∀Ci ,i∈[k ' ] Ci vi
vi v∈C ∃u∈Ci {u ,v}∈E
Rd ⊂R∖ S '
Rd =r1 ,... ,rl
{v1 ,... ,vk ' } {A1 ,... , Al }
ri Ai
Bk '
l≤k '≤k

22. 22
Distance to clique
• Proof: Algorithm “continue”:
- From G' ,build bipartite graph , H=( ,B)
where and where
there is an edge between and all
iff such that c(v)=x, v dominate and there
is no ,v dominate .
- H has vertices and in
can decided if H has perfect matching in
size l if exists [3].
H1∪H2
H1={uAi
,i∈[l]} H2= ∪
x∈M '
{ux
1
,ux
2
,... ,ux
mM ' x
}
uAi {ux
1,
ux
2,.
.. ,ux
mM ' x
}
∃v∈V ' Ai
i≠ j Aj
l+∣M '∣≤k+∣M∣ (k+ M )2.376

23. 23
Distance to clique
● Proof “continue”:
- Build a match from to where j is
smallest integer not yet in the match.
- Because ,j will not exceed .
U Ai
uc(ri)
j
c(R' )⊆M ' mM ' (c(ri))

24. 24
Distance to clique
• Proof: Algorithm “continue”:
- from perfect matching in H, graph MOTIF
solution built:
- there , namely ,
and dominate .
- set , G[Z] is connected and
and then we extend z by adding subset
such that c(Z')=M'c(Z).
∀i∈l {uAi
,ux
ji
}∈B ∃wi ∈V ' c(wi)=x
wi Ai
Z=S '∪∪
i∈l
wi c(Z )⊆M '
Z '⊆C ∖ Z

25. 25
Distance to clique
• Theorem: graph MOTIF can be solved in
where k is distance of input graph to clique.
• Proof: Algorithm “continue”:
- The algorithm needs:
- to compute vertex cover
- to build G' from G.
- to build H from G'.
- to check perfect matching in H.
- to build perfect matching in H.
- all together:
- As ,so the algorithm fulfill the above theorem.
O
∗
(2
klogk
)
(1.2738k
)
p1(n)
p2(n)
(k+∣M∣)
2.376
p3(n)
1.2738k
+ 2k
( p1(n)+ Bk ( p2(n)+ (k+∣M∣)
2.376
+ p3(n)))
BK < (
0.792k
ln(k+ 1)
)
k

26. 26
Vertex cover number

27. 27
Vertex cover number
● Theorem: Graph MOTIF can be solved in
on graph with vertex cover of size k.
● Proof: Algorithm:
-same previous algorithm but computing the vertex cover in G,
up to computing .
-we guess in time , compute the order pair
such that (1) dominate , (2) has at least one neighbor in
, (3) has no neighbor in .
O
∗
(2
2klog k
)
Rd =r1 ,... ,rl
O∗
(k ! Bk ) < A1, A2, .. , Al >
riAi
∪
1≤ j< i
Aj
ri
∪
i< j≤l
Aj
ri

28. 28
Vertex cover number
● Theorem: Graph MOTIF can be solved in
on graph with vertex cover of size k.
Proof: continue:
-in H={ } there is an edge between and
iff ,c(v)=x,v dominate , And v has one neighbor in
.
-if H has perfect matching, then we can build MOTIF solution.
- and , then the complexity is
O
∗
(2
2klog k
)
H1∪H 2 , B uAi {ux
1,
ux
2,.
.. ,ux
mM ' (x)
}
∃v∈V ' Ai
∪
1≤ j< i
Aj
k !≤k
k
Bk≤k
k O∗
(kk
∗kk
)=O∗
(22klogk
)

29. 29
Parameters which Graph
MOTIF is Hard

30. 30
Parameters which Graph MOTIF is
Hard
● Graph MOTIF problem still NP-Hard even if
provided with some parameters.
-Deletion set Number.

31. 31
Deletion set Number
Parameter

32. 32
Deletion set Number Parameter
● Definition:
minimum number of vertices to remove to make
graph belong to restricted class.
● Theorem:
Graph MOTIF is NP-Hard for graph with
distance 1 to disjoint paths and colorful motif.

33. 33
Deletion set Number Parameter
● Proof:
-Relation with X3C.
Given X={ },S={ }, find ,st.
each element in X exists only once in T.
From I=(X,S), construct I'=(G=(V,E),c,M) ,M
motif, by:
one root r , , two paths are built, first
including , three elements of , .second
includes .
x1, x2,.... , x3q S1, S2,.... ,S∣S∣ T ⊂S
∀Si ∈S
ai
1
Si
ai
2
,bi
2
bi
1

34. 34
Deletion set Number Parameter
C={1,2,...,2|S|+3q+1}.c( )=c( )=i. c( )=c( )=|S|+i for .
colors are assigned to nodes vertices according
to x,c(r)= .the construction is done in polynomial time.
ai
1 ai
2
ai
1 bi
1
bi
2
1≤i≤∣S∣
2∣S∣+ 1,... ,2∣S∣+ 3q
3q+ 2∣S∣+ 1

35. 35
Deletion set Number Parameter
C={1,2,...,2|S|+3q+1}.c( )=c( )=i. c( )=c( )=|S|+i for .
colors are assigned to nodes vertices according
to x,c(r)= .the construction is done in polynomial time.
ai
1 ai
2
ai
1 bi
1
bi
2
1≤i≤∣S∣
2∣S∣+ 1,... ,2∣S∣+ 3q
3q+ 2∣S∣+ 1

36. 36
Deletion set Number Parameter
• :
given is solution for I, build solution P for I':
-take root node.
- take the full path from to .
- take the path .
- all colors are taken only once.
T ⊂S
∀Si ∈T ai
1
bi
1
∀Si ∉T ai
2
bi
2
X3C ⇒ MOTIF

37. 37
Deletion set Number Parameter
• :
Given solution P for I' ,build solution for I.
- Root node is taken.
- For each either or is taken, same
for and .
- To add , should be added due to
connectivity constraint.
MOTIF ⇒ X3C
1≤i≤∣S∣ ai
1
ai
2
bi
1
bi
2
bi
2
ai
2
T ⊂S

38. 38
Deletion set Number Parameter
“continue”:
-either three nodes in are added or not.
-T={ }.since P is solution , no color
repeated and each element of X is appear
exactly once.
Si ∈S
Si∣ai
1
∈P
MOTIF ⇒ X3C

39. 39
Refrences
● [1] “R. Ganian. Using neighborhood diversity to solve hard
problems. CoRR, abs/1201.3091,2012.”.
● [2]M. Mucha and P. Sankowski. Maximum Matchings via
Gaussian Elimination. In 45th Sym-posium on Foundations of
Computer Science (FOCS 2004), pages 248–255. IEEE
ComputerSociety, 2004.
● [3] “J. Chen, I. A. Kanj, and G. Xia. Improved upper bounds for
vertex cover. Theoretical Computer Science, 411(4042):3736 –
3756, 2010.”

40. 40
Thank you for your
attention