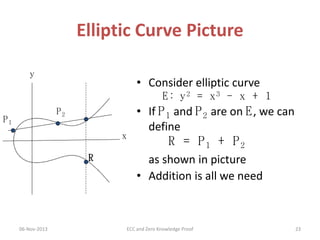
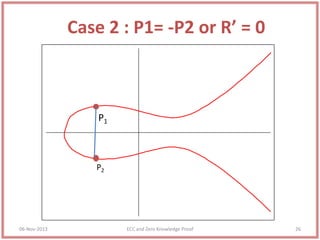
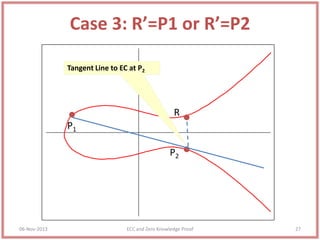
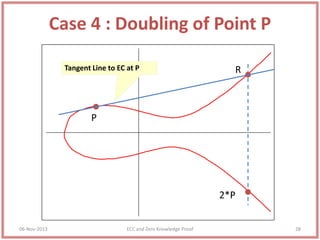
This document discusses elliptic curve cryptography and zero knowledge proofs. It begins by establishing the mathematical foundations needed for cryptography, including groups, rings, fields, and the discrete logarithm problem. It then explains how elliptic curves can be used in public key cryptography applications like Diffie-Hellman key exchange and ElGamal encryption. It also covers zero knowledge proofs, their properties, examples of uses, and the Fiat-Shamir identification protocol. Throughout, it provides examples to illustrate key concepts in elliptic curve cryptography and zero knowledge proofs.













![What Is Elliptic Curve Cryptography
(ECC)?
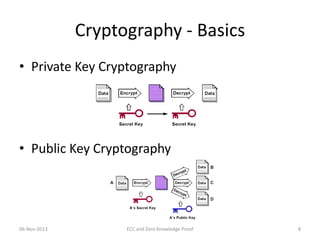
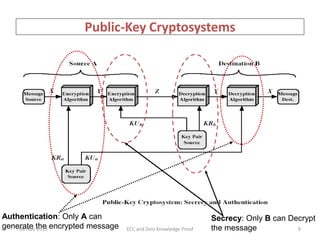
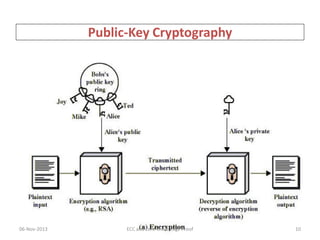
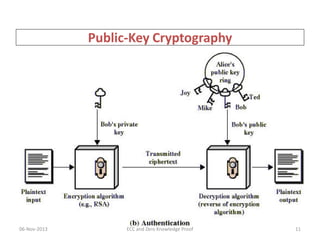
• Elliptic curve cryptography [ECC] is a public-key
cryptosystem just like RSA, Rabin, and El Gamal.
• Every user has a public and a private key.
– Public key is used for encryption/signature verification.
– Private key is used for decryption/signature generation.
• Elliptic curves are used as an extension to other
current cryptosystems.
06-Nov-2013
ECC and Zero Knowledge Proof
18](https://image.slidesharecdn.com/ellipticcurvecryptographyandzeroknowledgeproof-140128121940-phpapp01/85/Elliptic-curve-cryptography-and-zero-knowledge-proof-18-320.jpg)