More Related Content
PDF
Graph-to-Sequence Learning using Gated Graph Neural Networks. [ACL'18] 論文紹介 PDF
PDF
attention_is_all_you_need_nips17_論文紹介 PPTX
猫でも分かるVariational AutoEncoder PPTX
第3回nips読み会・関西『variational inference foundations and modern methods』 PDF
PDF
PDF
When NAS Meets Robustness:�In Search of Robust Architectures against�Adversar... What's hot
PPTX
[DL輪読会]GQNと関連研究,世界モデルとの関係について PPTX
[DL輪読会]QUASI-RECURRENT NEURAL NETWORKS PDF
PDF
Pythonによる機械学習入門 ~Deep Learningに挑戦~ PPTX
"There and Back Again: Revisiting Backpropagation Saliency Methods" (CVPR2020) PDF
PDF
PDF
When NAS Meets Robustness:�In Search of Robust Architectures against�Adversar... PDF
Introduction to Chainer (LL Ring Recursive) PDF
[DL輪読会]QUASI-RECURRENT NEURAL NETWORKS PDF
PPTX
PDF
PDF
Practical recommendations for gradient-based training of deep architectures PPTX
[DL輪読会]Flow-based Deep Generative Models PDF
PDF
Get To The Point: Summarization with Pointer-Generator Networks_acl17_論文紹介 PDF
JAWSDAYS 2014 ACEに聞け! EMR編 PPTX
[DL輪読会]Learning convolutional neural networks for graphs PPTX
Viewers also liked
PDF
PDF
PDF
PDF
CMSI計算科学技術特論A(10) 行列計算における高速アルゴリズム1 PDF
PDF
PDF
PDF
Map Reduce 〜入門編:仕組みの理解とアルゴリズムデザイン〜 Similar to Akira Imakura
PDF
PDF
El text.tokuron a(2019).yamamoto190627 PPTX
GPUによる多倍長整数乗算の高速化手法の提案とその評価 PDF
CMSI計算科学技術特論A (2015) 第11回 行列計算における高速アルゴリズム2 PDF
El text.tokuron a(2019).yamamoto190620 PPTX
PDF
PDF
PDF
CMSI計算科学技術特論A(11) 行列計算における高速アルゴリズム2 PDF
PDF
PDF
PDF
第15回 配信講義 計算科学技術特論B(2022) PDF
CMSI計算科学技術特論A (2015) 第10回 行列計算における高速アルゴリズム1 PDF
PDF
PPTX
PDF
20170408cvsaisentan6 2 4.3-4.5 PDF
Cvpr2011 reading-tsubosaka PDF
More from Suurist
PPTX
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
PDF
Akira Imakura
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
/ 56
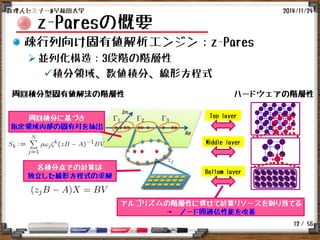
周回積分型固有値解法の概略
関連解法
原著論文とその改良法
その他の関連解法
FEAST eigensolver[Polizzi:2009]
Beyn法(非線形) [Beyn:2012]
2014/11/24数理人セミナー@早稲田大学
24
(原著論文)
[Sakurai&Sugiura:2003]
ブロック化に基づく
高安定化
[Ikegami et.al.:2010]
RR法に基づく
高精度化
[Sakurai&Tadano:2007]
ブロック化 + RR法
(SS-RR法)
[Ikegami&Sakurai:2010]
Arnoldi法に基づく
新解釈・新解法
(SS-Arnoldi法)
[I,Du&Sakurai:2014]
- 25.
- 26.
- 27.
- 28.
- 29.
/ 56
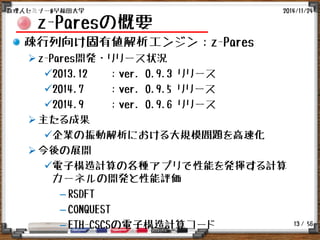
block SS-Hankel法の概略
blockSS-Hankel法 [Ikegami et al.:2010]
アルゴリズム
2014/11/24数理人セミナー@早稲田大学
29
Algorithm: block SS-Hankel
1. Compute basis vectors:
2. Construct block Hessenberg matrices
3. Compute low-rank approx. of :
4. Solve
and set
- 30.
- 31.
- 32.
/ 56
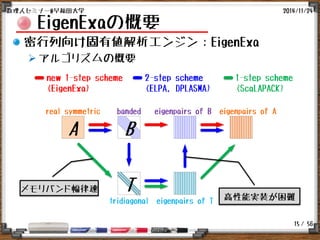
block SS-RR法の概略
blockSS-RR法 [Ikegami&Sakurai:2010]
アルゴリズム
2014/11/24数理人セミナー@早稲田大学
32
Algorithm: block SS-RR
1. Compute basis vectors:
2. Compute low-rank approx. of :
4. Solve
and set
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
/ 56
program user_code
usezpares
!<中略>
! 初期化
task = ZPARES_TASK_INIT
do while ( task /= ZPARES_TASK_FINISH )
! 固有値解析エンジン呼び出し
call zpares(task, work1, work2, …)
! taskにユーザーコード側の処理が指定される
if ( task == ZPARES_TASK_MATVEC )
! ユーザーの行列ベクトル積ルーチン呼び出し
call user_matvec(work1, work2)
else if ( task == ZPARES_TASK_SOLVE)
! ユーザーの線形ソルバルーチン呼び出し
call user_solver(work1, work2)
end if
end do
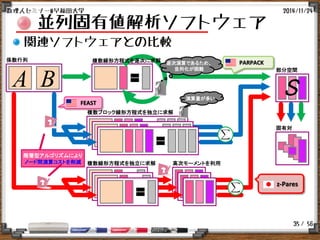
並列固有値解析ソフトウェア
RCI
2014/11/24数理人セミナー@早稲田大学
44
- 45.
/ 56
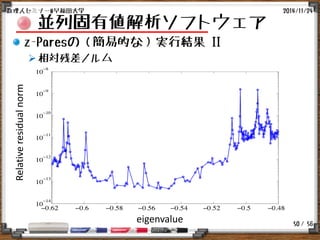
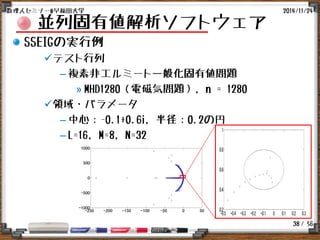
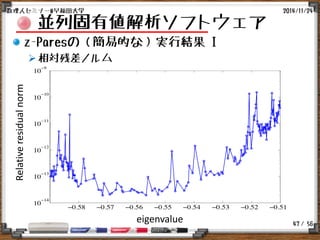
並列固有値解析ソフトウェア
z-Paresの(簡易的な)実行例 I
テスト行列
実対称・一般化固有値問題
–VCNT9000(ELSES Matrix Library)
– n=9,000, Nnz=3,464,136
領域・パラメータ
中心:-0.55, 半径:0.04, 半径比:0.1の楕円
L=32, M=16, N=32
線形方程式:MUMPUS
プロセス数:1, 2, 4, 8, 16(中位階層のみ並列化)
計算機環境
「京」, 1プロセス/1ノード
2014/11/24数理人セミナー@早稲田大学
45
- 46.
- 47.
- 48.
/ 56
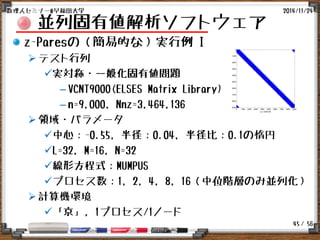
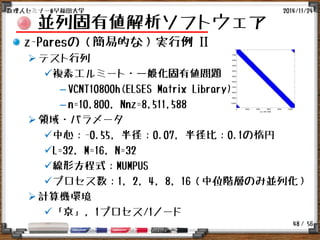
並列固有値解析ソフトウェア
z-Paresの(簡易的な)実行例 II
テスト行列
複素エルミート・一般化固有値問題
–VCNT10800h(ELSES Matrix Library)
– n=10,800, Nnz=8,511,588
領域・パラメータ
中心:-0.55, 半径:0.07, 半径比:0.1の楕円
L=32, M=16, N=32
線形方程式:MUMPUS
プロセス数:1, 2, 4, 8, 16(中位階層のみ並列化)
計算機環境
「京」, 1プロセス/1ノード
2014/11/24数理人セミナー@早稲田大学
48
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
- 55.
- 56.










![/ 56
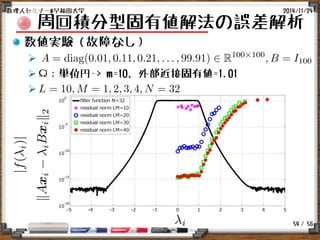
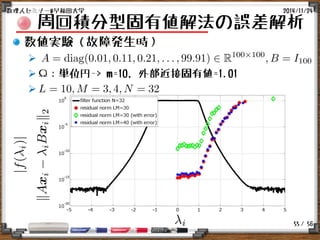
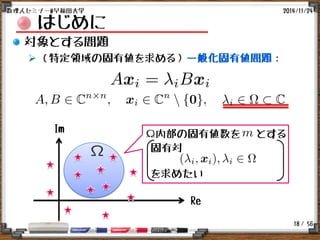
はじめに
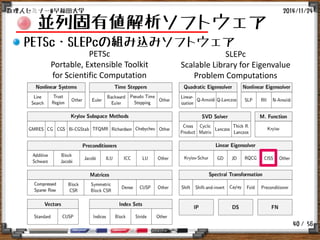
対象とする数値解法
周回積分型固有値解法:SS-RR法 [Sakurai&Sugiura:2003]
周回積分により対象の固有ベクトル成分を取り出す
関連解法
(block) SS-Hankel法
[Sakurai&Sugiura:2003,Ikegami et al.:2010]
(block) SS-RR法
[Sakurai&Tadano:2007,Ikegami&Sakurai:2010]
FEAST法 [Polizzi:2009]
block SS-Arnoldi法 [I,Du&Sakurai:2013]
Beyn法 [Beyn:2012] (非線形固有値問題向け)
2014/11/24数理人セミナー@早稲田大学
19](https://image.slidesharecdn.com/imakura-150108060513-conversion-gate01/85/Akira-Imakura-19-320.jpg)
![/ 56
周回積分型固有値解法の概略
基本的アイディア [Sakurai&Sugiura:2003]
一般化固有値問題の固有値を極に持つ有理関数
の領域Ω内の極をCauchyの積分公式
に基づく手法により計算する.ここで, ΓはJordan閉曲線
(Ωの境界)
2014/11/24数理人セミナー@早稲田大学
22](https://image.slidesharecdn.com/imakura-150108060513-conversion-gate01/85/Akira-Imakura-22-320.jpg)
![/ 56
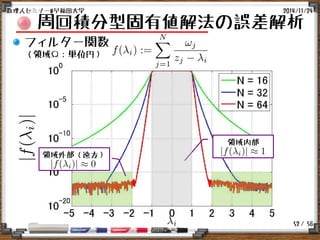
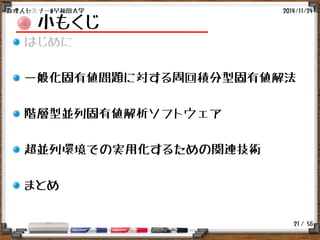
周回積分型固有値解法の概略
関数の領域Γ内部の極の計算 [Kravanja,Sakurai&van Barel:1999]
複素モーメント:
正則関数の領域Γ内部の極はHankel行列
を係数にもつ(小規模)一般化固有値問題
を解くことで得られる.
2014/11/24数理人セミナー@早稲田大学
23](https://image.slidesharecdn.com/imakura-150108060513-conversion-gate01/85/Akira-Imakura-23-320.jpg)
![/ 56
周回積分型固有値解法の概略
関連解法
原著論文とその改良法
その他の関連解法
FEAST eigensolver [Polizzi:2009]
Beyn法(非線形) [Beyn:2012]
2014/11/24数理人セミナー@早稲田大学
24
(原著論文)
[Sakurai&Sugiura:2003]
ブロック化に基づく
高安定化
[Ikegami et.al.:2010]
RR法に基づく
高精度化
[Sakurai&Tadano:2007]
ブロック化 + RR法
(SS-RR法)
[Ikegami&Sakurai:2010]
Arnoldi法に基づく
新解釈・新解法
(SS-Arnoldi法)
[I,Du&Sakurai:2014]](https://image.slidesharecdn.com/imakura-150108060513-conversion-gate01/85/Akira-Imakura-24-320.jpg)



![/ 56
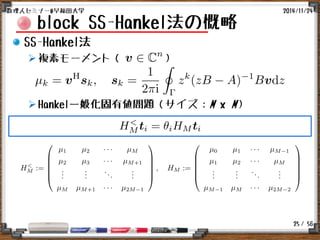
block SS-Hankel法の概略
block SS-Hankel法 [Ikegami et al.:2010]
アルゴリズム
2014/11/24数理人セミナー@早稲田大学
29
Algorithm: block SS-Hankel
1. Compute basis vectors:
2. Construct block Hessenberg matrices
3. Compute low-rank approx. of :
4. Solve
and set](https://image.slidesharecdn.com/imakura-150108060513-conversion-gate01/85/Akira-Imakura-29-320.jpg)


![/ 56
block SS-RR法の概略
block SS-RR法 [Ikegami&Sakurai:2010]
アルゴリズム
2014/11/24数理人セミナー@早稲田大学
32
Algorithm: block SS-RR
1. Compute basis vectors:
2. Compute low-rank approx. of :
4. Solve
and set](https://image.slidesharecdn.com/imakura-150108060513-conversion-gate01/85/Akira-Imakura-32-320.jpg)








![/ 56
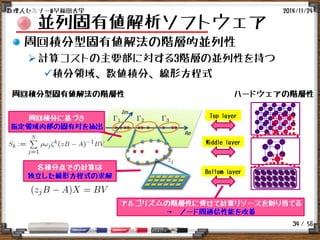
並列固有値解析ソフトウェア
z-Paresの(簡易的な)実行結果 I
並列性能
2014/11/24数理人セミナー@早稲田大学
46
0
10
20
30
40
50
60
1 2 4 8 16
misc Mult B
Mult A Small diag
Orth Solve
Fact
Elapsedtime[sec]
Number of Nodes](https://image.slidesharecdn.com/imakura-150108060513-conversion-gate01/85/Akira-Imakura-46-320.jpg)
![/ 56
並列固有値解析ソフトウェア
z-Paresの(簡易的な)実行結果 II
並列性能
2014/11/24数理人セミナー@早稲田大学
49
Elapsedtime[sec]
Number of Nodes
0
20
40
60
80
100
120
140
160
180
1 2 4 8 16
misc Mult B
Mult A Small diag
Orth Solve
Fact](https://image.slidesharecdn.com/imakura-150108060513-conversion-gate01/85/Akira-Imakura-49-320.jpg)