This document summarizes a presentation on rigorously verifying the accuracy of numerical solutions to semi-linear parabolic partial differential equations using analytic semigroups. It introduces the considered problem of finding the solution to a semi-linear parabolic PDE. It then discusses using a piecewise linear finite element discretization in space and time to obtain an initial numerical solution. The goal is to rigorously enclose the true solution within a radius ρ of this numerical solution in the function space L∞(J;H10(Ω)). Key steps involve using properties of the analytic semigroup generated by the operator A and estimating discretization errors to compute the enclosure radius ρ.

1. 解析半群を用いた半線形放物型
方程式の解に対する精度保証付
き数値計算法とその応用
高安 亮紀
早稲田大学 基幹理工学部 応用数理学科
第 3 回 数理人セミナー＠早稲田大学西早稲田キャンパス
2015 年 1 月 15 日
1/55

2. 自己紹介
高安亮紀
早稲田大学 応用数理学科
助教（大石研究室）
分野：(偏微分方程式の) 数値解析，
精度保証付き数値計算
2/55

3. 計算機を用いた
非線形PDEへの
解析アプローチ
3/55

4. 共同研究者
▶ 水口 信
（早稲田大学 基幹理工学研究科 数学応用数理専攻）
▶ 久保 隆徹
（筑波大学 数理物質系）
▶ 大石 進一
（早稲田大学 基幹理工学部 応用数理学科）
4/55

5. 半線形放物型方程式
Let Ω be a bounded polygonal domain in R2
.
(PJ )



∂tu + Au = f(u) in J × Ω,
u(t, x) = 0 on J × ∂Ω,
u(t0, x) = u0(x) in Ω,
▶ J := (t0, t1], 0 ≤ t0 < t1 < ∞ or J := (0, ∞),
▶ f : twice differentiable nonlinear mapping,
▶ u = 0 on ∂Ω is the trace sense,
▶ u0 ∈ H1
0 (Ω).
Lp
(Ω): the set of Lp
-functions,
H1
(Ω): the first order Sobolev space of L2
(Ω),
H1
0 (Ω) := {v ∈ H1
(Ω) : v = 0 on ∂Ω}.
5/55

6. 記号
A : D(A) ⊂ H1
0 (Ω) → L2
(Ω) is defined by
A := −
∑
1≤i,j≤2
∂
∂xj
(
aij(x)
∂
∂xi
)
,
where aij(x) = aji(x) is in W1,∞
(Ω) and satisfies
∑
1≤i,j≤2
aij(x)ξiξj ≥ µ|ξ|2
, ∀x ∈ Ω, ∀ξ ∈ R2
with µ > 0.
6/55

7. 記号
We endow L2
(Ω) with the inner product:
(u, v)L2 :=
∫
Ω
u(x)v(x)dx.
Use the usual norms:
∥u∥L2 :=
√
(u, u)L2 , ∥u∥H1
0
:= ∥∇u∥L2 ,
and
∥u∥H−1 := sup
0̸=v∈H1
0 (Ω)
∥v∥H1
0
=1
|⟨u, v⟩| ,
where ⟨·, ·⟩ is a dual product between H1
0 (Ω) and H−1
(Ω)1
.
1
The topological dual space of H1
0 (Ω).
7/55

8. 精度保証付き数値計算
(PJ ) の弱解: For t ∈ J, u(t) := u(t, ·) ∈ H1
0 (Ω) with the
initial function u0 such that
(∂tu(t), v)L2 + a(u(t), v) = (f(u(t)), v)L2 , ∀v ∈ H1
0 (Ω),
where a : H1
0 (Ω) × H1
0 (Ω) → R is a bilinear form:
a(u, v) :=
∑
1≤i,j≤2
(
aij(x)
∂u
∂xi
,
∂v
∂xj
)
L2
satisfying
a(u, u) ≥ µ∥u∥2
H1
0
, ∀u ∈ H1
0 (Ω),
|a(u, v)| ≤ M∥u∥H1
0
∥v∥H1
0
, ∀u, v ∈ H1
0 (Ω).
8/55

9. 精度保証付き数値計算
(PJ ) の弱解: For t ∈ J, u(t) := u(t, ·) ∈ H1
0 (Ω) with the
initial function u0 such that
(∂tu(t), v)L2 + a(u(t), v) = (f(u(t)), v)L2 , ∀v ∈ H1
0 (Ω),
where a : H1
0 (Ω) × H1
0 (Ω) → R is a bilinear form:
a(u, v) :=
∑
1≤i,j≤2
(
aij(x)
∂u
∂xi
,
∂v
∂xj
)
L2
satisfying
a(u, u) ≥ µ∥u∥2
H1
0
, ∀u ∈ H1
0 (Ω),
|a(u, v)| ≤ M∥u∥H1
0
∥v∥H1
0
, ∀u, v ∈ H1
0 (Ω).
8/55

10. 精度保証付き数値計算
(PJ ) の弱解: For t ∈ J, u(t) := u(t, ·) ∈ H1
0 (Ω) with the
initial function u0 such that
(∂tu(t), v)L2 + a(u(t), v) = (f(u(t)), v)L2 , ∀v ∈ H1
0 (Ω),
where a : H1
0 (Ω) × H1
0 (Ω) → R is a bilinear form:
a(u, v) :=
∑
1≤i,j≤2
(
aij(x)
∂u
∂xi
,
∂v
∂xj
)
L2
satisfying
a(u, u) ≥ µ∥u∥2
H1
0
, ∀u ∈ H1
0 (Ω),
|a(u, v)| ≤ M∥u∥H1
0
∥v∥H1
0
, ∀u, v ∈ H1
0 (Ω).
8/55

11. 精度保証付き数値計算
問題 (PJ ) の弱解の存在と一意性を計算機を援用し証明する．
すなわち X を J × Ω 上のある Banach 空間とし，弱解を数
値解 ω を中心とする閉球:
BJ (ω, ρ) := {v ∈ X : ∥v − ω∥X ≤ ρ}.
内に数学的に厳密に包み込む．
9/55

12. 精度保証付き数値計算に関する先行研究
M.T. Nakao, T. Kinoshita and T. Kimura,
“On a posteriori estimates of inverse operators for linear
parabolic initial-boundary value problems”, Computing
94(2-4), 151–162, 2012.
M.T. Nakao, T. Kimura and T. Kinoshita,
“Constructive A Priori Error Estimates for a Full Discrete
Approximation of the Heat Equation”, Siam J. Numer. Anal.,
51(3), 1525–1541, 2013.
T. Kinoshita, T. Kimura and M.T. Nakao,
“On the a posteriori estimates for inverse operators of linear
parabolic equations with applications to the numerical
enclosure of solutions for nonlinear problems”, Numer. Math,
Online First, 2013.
10/55

13. 力学系の観点からみた研究
P. Zgliczy´nski and K. Mischaikow,
“Rigorous Numerics for Partial Differential Equations: The
Kuramoto―Sivashinsky Equation”, Foundations of
Computational Mathematics, 1(3), 1615–3375, 2001.
P. Zgliczy´nski,
“Rigorous numerics for dissipative PDEs III. An effective
algorithm for rigorous integration of dissipative PDEs”, Topol.
Methods Nonlinear Anal., 36, 197–262, 2010.
11/55

14. 離散半群を用いた数値スキームの研究
H. Fujita,
“On the semi-discrete finite element approximation for the
evolution equation ut + A(t)u = 0 of parabolic type”, Topics
in numerical analysis III, Academic Press, 143–157, 1977.
H. Fujita and A. Mizutani,
“On the finite element method for parabolic equations, I;
approximation of holomorphic semi-groups”, J. Math. Soc.
Japan, 28, 749–771, 1976.
H. Fujita, N. Saito and T. Suzuki,
“Operator theory and numerical methods”, Elsevier(Holland),
308pages, 2001.
12/55

15. Concatenation scheme
13/55

16. Considered problem
J := (t0, t1] : arbitrary time interval. τ := t1 − t0.
(PJ )



∂tu + Au = f(u) in J × Ω,
u(t, x) = 0 on J × ∂Ω,
u(t0, x) = u0(x) in Ω,
where u0 is an initial function in H1
0 (Ω).
Vh ⊂ H1
0 (Ω) : a finite dimensional subspace.
Starts from: ˆu0, ˆu1 ∈ Vh
ω(t) = ˆu0ϕ0(t) + ˆu1ϕ1(t), t ∈ J,
where ϕk(t) is a piecewise linear Lagrange basis: ϕk(tj) = δkj
(δkj is a Kronecker’s delta).
14/55

17. Considered problem
J := (t0, t1] : arbitrary time interval. τ := t1 − t0.
(PJ )



∂tu + Au = f(u) in J × Ω,
u(t, x) = 0 on J × ∂Ω,
u(t0, x) = u0(x) in Ω,
where u0 is an initial function in H1
0 (Ω).
Vh ⊂ H1
0 (Ω) : a finite dimensional subspace.
Starts from: ˆu0, ˆu1 ∈ Vh
ω(t) = ˆu0ϕ0(t) + ˆu1ϕ1(t), t ∈ J,
where ϕk(t) is a piecewise linear Lagrange basis: ϕk(tj) = δkj
(δkj is a Kronecker’s delta).
14/55

18. Considered problem
Let the initial function satisfy
∥u0 − ˆu0∥H1
0
≤ ε0.
We rigorously enclose the solution in a Banach space2
,
L∞
(
J; H1
0 (Ω)
)
:=
{
u(t) ∈ H1
0 (Ω) : ess sup
t∈J
∥u(t)∥H1
0
< ∞
}
.
Namely, we compute a radius ρ > 0 of the ball:
BJ (ω, ρ) :=
{
y ∈ L∞
(
J; H1
0 (Ω)
)
: ∥y − ω∥L∞
(J;H1
0 (Ω)) ≤ ρ
}
.
2
∥u∥L∞(J;H1
0 (Ω)) := ess supt∈J ∥u(t)∥H1
0
15/55

19. Considered problem
Let the initial function satisfy
∥u0 − ˆu0∥H1
0
≤ ε0.
We rigorously enclose the solution in a Banach space2
,
L∞
(
J; H1
0 (Ω)
)
:=
{
u(t) ∈ H1
0 (Ω) : ess sup
t∈J
∥u(t)∥H1
0
< ∞
}
.
Namely, we compute a radius ρ > 0 of the ball:
BJ (ω, ρ) :=
{
y ∈ L∞
(
J; H1
0 (Ω)
)
: ∥y − ω∥L∞
(J;H1
0 (Ω)) ≤ ρ
}
.
2
∥u∥L∞(J;H1
0 (Ω)) := ess supt∈J ∥u(t)∥H1
0
15/55

20. Considered problem
Let the initial function satisfy
∥u0 − ˆu0∥H1
0
≤ ε0.
We rigorously enclose the solution in a Banach space2
,
L∞
(
J; H1
0 (Ω)
)
:=
{
u(t) ∈ H1
0 (Ω) : ess sup
t∈J
∥u(t)∥H1
0
< ∞
}
.
Namely, we compute a radius ρ > 0 of the ball:
BJ (ω, ρ) :=
{
y ∈ L∞
(
J; H1
0 (Ω)
)
: ∥y − ω∥L∞
(J;H1
0 (Ω)) ≤ ρ
}
.
2
∥u∥L∞(J;H1
0 (Ω)) := ess supt∈J ∥u(t)∥H1
0
15/55

21. Analytic semigroup
The weak form of A, which is denoted by −A3
, generates the
analytic semigroup {e−tA
}t≥0 over H−1
(Ω). The following
abstract problem has an unique solution:
∂tu + Au = 0, u(0, x) = u0 =⇒ ∃u = e−tA
u0.
Fact
Let x ∈ D(A) and λ0 be a positive number. A satisfies
⟨−Ax, x⟩ ≤ 0, R(λ0I + A) = H−1
(Ω).
Then, there exists an analytic semigroup {e−tA
}t≥0 generated by −A.
Proofs are found in several textbooks.
3
A : H1
0 (Ω) → H−1
(Ω) s.t. ⟨Au, v⟩ := a(u, v), ∀v ∈ H1
0 (Ω).
16/55

22. Theorem
Assume that the initial function u0 satisfies ∥u0 − ˆu0∥H1
0
≤ ε0;
Assume that ω satisfies the following estimate:
∫ t
t0
e−(t−s)A
(∂tω(s) + Aω(s) − f(ω(s)))ds
L∞
(J;H1
0 (Ω))
≤ δ.
Assume that, for ∀ρ0 ∈ (0, ρ] with a certain ρ 0, f satisfies
∥f(φ) − f(ψ)∥L∞(J;L2(Ω)) ≤ Lρ0 ∥φ − ψ∥L∞
(J;H1
0 (Ω)),
where ∀φ, ψ ∈ BJ (ω, ρ0) ⊂ L∞
(J; H1
0 (Ω)). If
M
µ
ε0 +
2
µ
√
Mτ
e
Lρρ + δ ρ,
then the weak solution u(t), t ∈ J of (PJ ) uniquely exists in
the ball BJ (ω, ρ).
17/55

23. Theorem
Assume that the initial function u0 satisfies ∥u0 − ˆu0∥H1
0
≤ ε0;
Assume that ω satisfies the following estimate:
∫ t
t0
e−(t−s)A
(∂tω(s) + Aω(s) − f(ω(s)))ds
L∞
(J;H1
0 (Ω))
≤ δ.
Assume that, for ∀ρ0 ∈ (0, ρ] with a certain ρ 0, f satisfies
∥f(φ) − f(ψ)∥L∞(J;L2(Ω)) ≤ Lρ0 ∥φ − ψ∥L∞
(J;H1
0 (Ω)),
where ∀φ, ψ ∈ BJ (ω, ρ0) ⊂ L∞
(J; H1
0 (Ω)). If
M
µ
ε0 +
2
µ
√
Mτ
e
Lρρ + δ ρ,
then the weak solution u(t), t ∈ J of (PJ ) uniquely exists in
the ball BJ (ω, ρ).
17/55

24. Theorem
Assume that the initial function u0 satisfies ∥u0 − ˆu0∥H1
0
≤ ε0;
Assume that ω satisfies the following estimate:
∫ t
t0
e−(t−s)A
(∂tω(s) + Aω(s) − f(ω(s)))ds
L∞
(J;H1
0 (Ω))
≤ δ.
Assume that, for ∀ρ0 ∈ (0, ρ] with a certain ρ 0, f satisfies
∥f(φ) − f(ψ)∥L∞(J;L2(Ω)) ≤ Lρ0 ∥φ − ψ∥L∞
(J;H1
0 (Ω)),
where ∀φ, ψ ∈ BJ (ω, ρ0) ⊂ L∞
(J; H1
0 (Ω)). If
M
µ
ε0 +
2
µ
√
Mτ
e
Lρρ + δ ρ,
then the weak solution u(t), t ∈ J of (PJ ) uniquely exists in
the ball BJ (ω, ρ).
17/55

25. Theorem
Assume that the initial function u0 satisfies ∥u0 − ˆu0∥H1
0
≤ ε0;
Assume that ω satisfies the following estimate:
∫ t
t0
e−(t−s)A
(∂tω(s) + Aω(s) − f(ω(s)))ds
L∞
(J;H1
0 (Ω))
≤ δ.
Assume that, for ∀ρ0 ∈ (0, ρ] with a certain ρ 0, f satisfies
∥f(φ) − f(ψ)∥L∞(J;L2(Ω)) ≤ Lρ0 ∥φ − ψ∥L∞
(J;H1
0 (Ω)),
where ∀φ, ψ ∈ BJ (ω, ρ0) ⊂ L∞
(J; H1
0 (Ω)). If
M
µ
ε0 +
2
µ
√
Mτ
e
Lρρ + δ ρ,
then the weak solution u(t), t ∈ J of (PJ ) uniquely exists in
the ball BJ (ω, ρ).
17/55

26. Theorem
Assume that the initial function u0 satisfies ∥u0 − ˆu0∥H1
0
≤ ε0;
Assume that ω satisfies the following estimate:
∫ t
t0
e−(t−s)A
(∂tω(s) + Aω(s) − f(ω(s)))ds
L∞
(J;H1
0 (Ω))
≤ δ.
Assume that, for ∀ρ0 ∈ (0, ρ] with a certain ρ 0, f satisfies
∥f(φ) − f(ψ)∥L∞(J;L2(Ω)) ≤ Lρ0 ∥φ − ψ∥L∞
(J;H1
0 (Ω)),
where ∀φ, ψ ∈ BJ (ω, ρ0) ⊂ L∞
(J; H1
0 (Ω)). If
M
µ
ε0 +
2
µ
√
Mτ
e
Lρρ + δ ρ,
then the weak solution u(t), t ∈ J of (PJ ) uniquely exists in
the ball BJ (ω, ρ).
17/55

27. Sketch of proof
Let z(t) ∈ H1
0 (Ω) for t ∈ J. We put u(t) = ω(t) + z(t).
For any v ∈ H1
0 (Ω),
(∂tz(t), v)L2 + a(z(t), v)
= (f(u(t)), v)L2 − ((∂tω(t), v)L2 + ⟨Aω(t), v⟩)
=: ⟨g(z(t)), v⟩ ,
where g(z(t)) = f(u(t)) − (∂tω(t) + Aω(t)). Note that by
the definition of the natural embedding L2
(Ω) → H−1
(Ω),
(ψ, v)L2 = ⟨ψ, v⟩ holds for ψ ∈ L2
(Ω).
Define S : L∞
(J; H1
0 (Ω)) → L∞
(J; H1
0 (Ω)) using the
analytic semigroup e−tA
as
S(z) := e−(t−t0)A
(u0 − ˆu0) +
∫ t
t0
e−(t−s)A
g(z(s))ds.
18/55

28. Sketch of proof
Let z(t) ∈ H1
0 (Ω) for t ∈ J. We put u(t) = ω(t) + z(t).
For any v ∈ H1
0 (Ω),
(∂tz(t), v)L2 + a(z(t), v)
= (f(u(t)), v)L2 − ((∂tω(t), v)L2 + ⟨Aω(t), v⟩)
=: ⟨g(z(t)), v⟩ ,
where g(z(t)) = f(u(t)) − (∂tω(t) + Aω(t)). Note that by
the definition of the natural embedding L2
(Ω) → H−1
(Ω),
(ψ, v)L2 = ⟨ψ, v⟩ holds for ψ ∈ L2
(Ω).
Define S : L∞
(J; H1
0 (Ω)) → L∞
(J; H1
0 (Ω)) using the
analytic semigroup e−tA
as
S(z) := e−(t−t0)A
(u0 − ˆu0) +
∫ t
t0
e−(t−s)A
g(z(s))ds.
18/55

29. Sketch of proof
For ρ 0, Z := {z : ∥z∥L∞
(J;H1
0 (Ω)) ≤ ρ} ⊂ L∞
(J; H1
0 (Ω)).
On the basis of Banach’s fixed-point theorem, we show a
sufficient condition of S having a fixed-point in Z.
S(Z) ⊂ Z Since the analytic semigroup e−tA
is bounded,
the first term of S(z) is estimated4
by
e−(t−t0)A
(ζ − ˆu0) H1
0
≤ µ−1
A e−(t−t0)A
(ζ − ˆu0) H−1
≤
M
µ
e−(t−t0)λmin
ε0.
Then
e−(t−t0)A
(ζ − ˆu0) L∞(J;H1
0 (Ω))
≤
M
µ
ε0.
4
µ∥u∥H1
0
≤ ∥Au∥H−1 ≤ M∥u∥H1
0
is used.
19/55

30. Sketch of proof
For ρ 0, Z := {z : ∥z∥L∞
(J;H1
0 (Ω)) ≤ ρ} ⊂ L∞
(J; H1
0 (Ω)).
On the basis of Banach’s fixed-point theorem, we show a
sufficient condition of S having a fixed-point in Z.
S(Z) ⊂ Z Since the analytic semigroup e−tA
is bounded,
the first term of S(z) is estimated4
by
e−(t−t0)A
(ζ − ˆu0) H1
0
≤ µ−1
A e−(t−t0)A
(ζ − ˆu0) H−1
≤
M
µ
e−(t−t0)λmin
ε0.
Then
e−(t−t0)A
(ζ − ˆu0) L∞(J;H1
0 (Ω))
≤
M
µ
ε0.
4
µ∥u∥H1
0
≤ ∥Au∥H−1 ≤ M∥u∥H1
0
is used.
19/55

31. Sketch of proof
For ρ 0, Z := {z : ∥z∥L∞
(J;H1
0 (Ω)) ≤ ρ} ⊂ L∞
(J; H1
0 (Ω)).
On the basis of Banach’s fixed-point theorem, we show a
sufficient condition of S having a fixed-point in Z.
S(Z) ⊂ Z Since the analytic semigroup e−tA
is bounded,
the first term of S(z) is estimated4
by
e−(t−t0)A
(ζ − ˆu0) H1
0
≤ µ−1
A e−(t−t0)A
(ζ − ˆu0) H−1
≤
M
µ
e−(t−t0)λmin
ε0.
Then
e−(t−t0)A
(ζ − ˆu0) L∞(J;H1
0 (Ω))
≤
M
µ
ε0.
4
µ∥u∥H1
0
≤ ∥Au∥H−1 ≤ M∥u∥H1
0
is used.
19/55

32. Sketch of proof
Decompose g(z(s)) ∈ H−1
(Ω) into two parts:
g(z(s)) = f(ω(s) + z(s)) − (∂tω(s) + Aω(s))
= g1(s) + g2(s),
g1(s) := f(ω(s) + z(s)) − f(ω(s)),
g2(s) := f(ω(s)) − (∂tω(s) + Aω(s)) .
Put
ν(t) :=
∫ t
t0
(t − s)−1
2 e−1
2
(t−s)λmin
ds,
sup
t∈J
ν(t) ≤ sup
t∈J
∫ t
t0
(t − s)− 1
2 ds = 2
√
τ.
Furthermore, ready an inequality
µ
1
2 ∥u∥L2 ≤ ∥A
1
2 u∥H−1 ≤ M
1
2 ∥u∥L2 .
20/55

33. Sketch of proof
Decompose g(z(s)) ∈ H−1
(Ω) into two parts:
g(z(s)) = f(ω(s) + z(s)) − (∂tω(s) + Aω(s))
= g1(s) + g2(s),
g1(s) := f(ω(s) + z(s)) − f(ω(s)),
g2(s) := f(ω(s)) − (∂tω(s) + Aω(s)) .
Put
ν(t) :=
∫ t
t0
(t − s)−1
2 e−1
2
(t−s)λmin
ds,
sup
t∈J
ν(t) ≤ sup
t∈J
∫ t
t0
(t − s)− 1
2 ds = 2
√
τ.
Furthermore, ready an inequality
µ
1
2 ∥u∥L2 ≤ ∥A
1
2 u∥H−1 ≤ M
1
2 ∥u∥L2 .
20/55

34. Sketch of proof
Decompose g(z(s)) ∈ H−1
(Ω) into two parts:
g(z(s)) = f(ω(s) + z(s)) − (∂tω(s) + Aω(s))
= g1(s) + g2(s),
g1(s) := f(ω(s) + z(s)) − f(ω(s)),
g2(s) := f(ω(s)) − (∂tω(s) + Aω(s)) .
Put
ν(t) :=
∫ t
t0
(t − s)−1
2 e−1
2
(t−s)λmin
ds,
sup
t∈J
ν(t) ≤ sup
t∈J
∫ t
t0
(t − s)− 1
2 ds = 2
√
τ.
Furthermore, ready an inequality
µ
1
2 ∥u∥L2 ≤ ∥A
1
2 u∥H−1 ≤ M
1
2 ∥u∥L2 .
20/55

35. Sketch of proof
The term of g1(s):
∫ t
t0
e−(t−s)A
g1(s)ds
H1
0
=
∫ t
t0
e−(t−s)A
(f(ω(s) + z(s)) − f(ω(s)))ds
H1
0
≤ µ−1
∫ t
t0
A e−(t−s)A
(f(ω(s) + z(s)) − f(ω(s)))
H−1
ds
= µ−1
∫ t
t0
A
1
2 e−(t−s)A
A
1
2 (f(ω(s) + z(s)) − f(ω(s)))
H−1
ds
≤ µ−1
e− 1
2
∫ t
t0
(t − s)− 1
2 e− 1
2 (t−s)λmin
A
1
2 (f(ω(s) + z(s)) − f(ω(s)))
H−1
≤ µ−1
M
1
2 e− 1
2
∫ t
t0
(t − s)− 1
2 e− 1
2 (t−s)λmin
∥f(ω(s) + z(s)) − f(ω(s))∥L2 ds
≤ µ−1
M
1
2 e− 1
2 ν(t) ∥f(ω + z) − f(ω)∥L∞(J;L2(Ω)).
21/55

36. Sketch of proof
Then
∫ t
t0
e−(t−s)A
g1(s)ds
L∞
(J;H1
0 (Ω))
≤
2
µ
√
Mτ
e
Lρρ.
The term of g2(s) is nothing but the residual of the
approximate solution, which is estimated by δ.
Then it follows
∥S(z)∥L∞
(J;H1
0 (Ω)) ≤
M
µ
ε0 +
2
µ
√
Mτ
e
L(ρ)ρ + δ.
∥S(z)∥L∞
(J;H1
0 (Ω)) ρ holds from the condition of the
theorem. It implies that S(z) ∈ Z.
22/55

37. Sketch of proof
Then
∫ t
t0
e−(t−s)A
g1(s)ds
L∞
(J;H1
0 (Ω))
≤
2
µ
√
Mτ
e
Lρρ.
The term of g2(s) is nothing but the residual of the
approximate solution, which is estimated by δ.
Then it follows
∥S(z)∥L∞
(J;H1
0 (Ω)) ≤
M
µ
ε0 +
2
µ
√
Mτ
e
L(ρ)ρ + δ.
∥S(z)∥L∞
(J;H1
0 (Ω)) ρ holds from the condition of the
theorem. It implies that S(z) ∈ Z.
22/55

38. Sketch of proof
Then
∫ t
t0
e−(t−s)A
g1(s)ds
L∞
(J;H1
0 (Ω))
≤
2
µ
√
Mτ
e
Lρρ.
The term of g2(s) is nothing but the residual of the
approximate solution, which is estimated by δ.
Then it follows
∥S(z)∥L∞
(J;H1
0 (Ω)) ≤
M
µ
ε0 +
2
µ
√
Mτ
e
L(ρ)ρ + δ.
∥S(z)∥L∞
(J;H1
0 (Ω)) ρ holds from the condition of the
theorem. It implies that S(z) ∈ Z.
22/55

39. Sketch of proof
Then
∫ t
t0
e−(t−s)A
g1(s)ds
L∞
(J;H1
0 (Ω))
≤
2
µ
√
Mτ
e
Lρρ.
The term of g2(s) is nothing but the residual of the
approximate solution, which is estimated by δ.
Then it follows
∥S(z)∥L∞
(J;H1
0 (Ω)) ≤
M
µ
ε0 +
2
µ
√
Mτ
e
L(ρ)ρ + δ.
∥S(z)∥L∞
(J;H1
0 (Ω)) ρ holds from the condition of the
theorem. It implies that S(z) ∈ Z.
22/55

40. Sketch of proof
For any z1, z2 in Z,
S(z1) − S(z2) =
∫ t
t0
e−(t−s)A
(f(z1 + ω) − f(z2 + ω))ds
holds. We have
∫ t
t0
e−(t−s)A
(f(z1 + ω) − f(z2 + ω))ds
H1
0
≤ µ−1
M
1
2 e−1
2 ν(t)∥f(z1 + ω) − f(z2 + ω)∥L∞(J;L2(Ω)).
Here, zi + ω ∈ B(ω, ρ) (i = 1, 2) holds. Then
∥S(z1) − S(z2)∥L∞
(J;H1
0 (Ω)) ≤
2
µ
√
Mτ
e
Lρ∥z1 − z2∥L∞
(J;H1
0 (Ω)).
23/55

41. Sketch of proof
For any z1, z2 in Z,
S(z1) − S(z2) =
∫ t
t0
e−(t−s)A
(f(z1 + ω) − f(z2 + ω))ds
holds. We have
∫ t
t0
e−(t−s)A
(f(z1 + ω) − f(z2 + ω))ds
H1
0
≤ µ−1
M
1
2 e−1
2 ν(t)∥f(z1 + ω) − f(z2 + ω)∥L∞(J;L2(Ω)).
Here, zi + ω ∈ B(ω, ρ) (i = 1, 2) holds. Then
∥S(z1) − S(z2)∥L∞
(J;H1
0 (Ω)) ≤
2
µ
√
Mτ
e
Lρ∥z1 − z2∥L∞
(J;H1
0 (Ω)).
23/55

42. Sketch of proof
For any z1, z2 in Z,
S(z1) − S(z2) =
∫ t
t0
e−(t−s)A
(f(z1 + ω) − f(z2 + ω))ds
holds. We have
∫ t
t0
e−(t−s)A
(f(z1 + ω) − f(z2 + ω))ds
H1
0
≤ µ−1
M
1
2 e−1
2 ν(t)∥f(z1 + ω) − f(z2 + ω)∥L∞(J;L2(Ω)).
Here, zi + ω ∈ B(ω, ρ) (i = 1, 2) holds. Then
∥S(z1) − S(z2)∥L∞
(J;H1
0 (Ω)) ≤
2
µ
√
Mτ
e
Lρ∥z1 − z2∥L∞
(J;H1
0 (Ω)).
23/55

43. Sketch of proof
The condition of theorem also implies
2
µ
√
Mτ
e
L (ρ) 1.
Therefore, S is a contraction mapping. Banach’s fixed point
theorem yields that there uniquely exists a fixed-point in Z.
24/55

44. Theorem (A posteriori error estimate)
Assume that existence and local uniqueness of the weak
solution u(t), t ∈ J, is proved in BJ (ω, ρ). Assume also that
ω satisfies
∫ t1
t0
e−(t1−s)A
(∂tω(s) + Aω(s) − f(ω(s))) ds
H1
0
≤ ˜δ.
Then, the following a posteriori error estimate holds:
∥u(t1) − ˆu1∥H1
0
≤
M
µ
e−τλmin
ε0 +
2
µ
√
Mτ
e
Lρρ + ˜δ =: ε1.
25/55

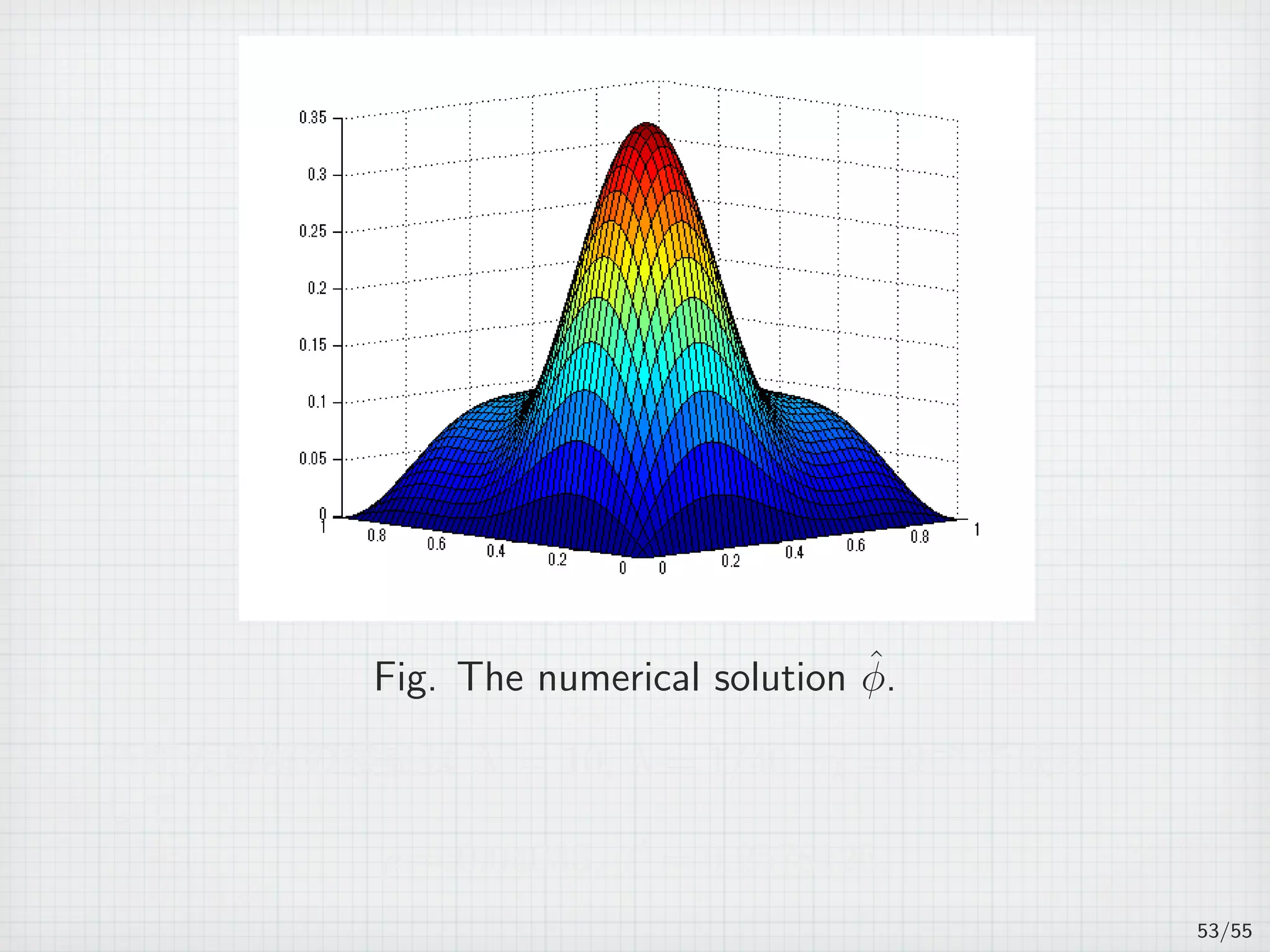
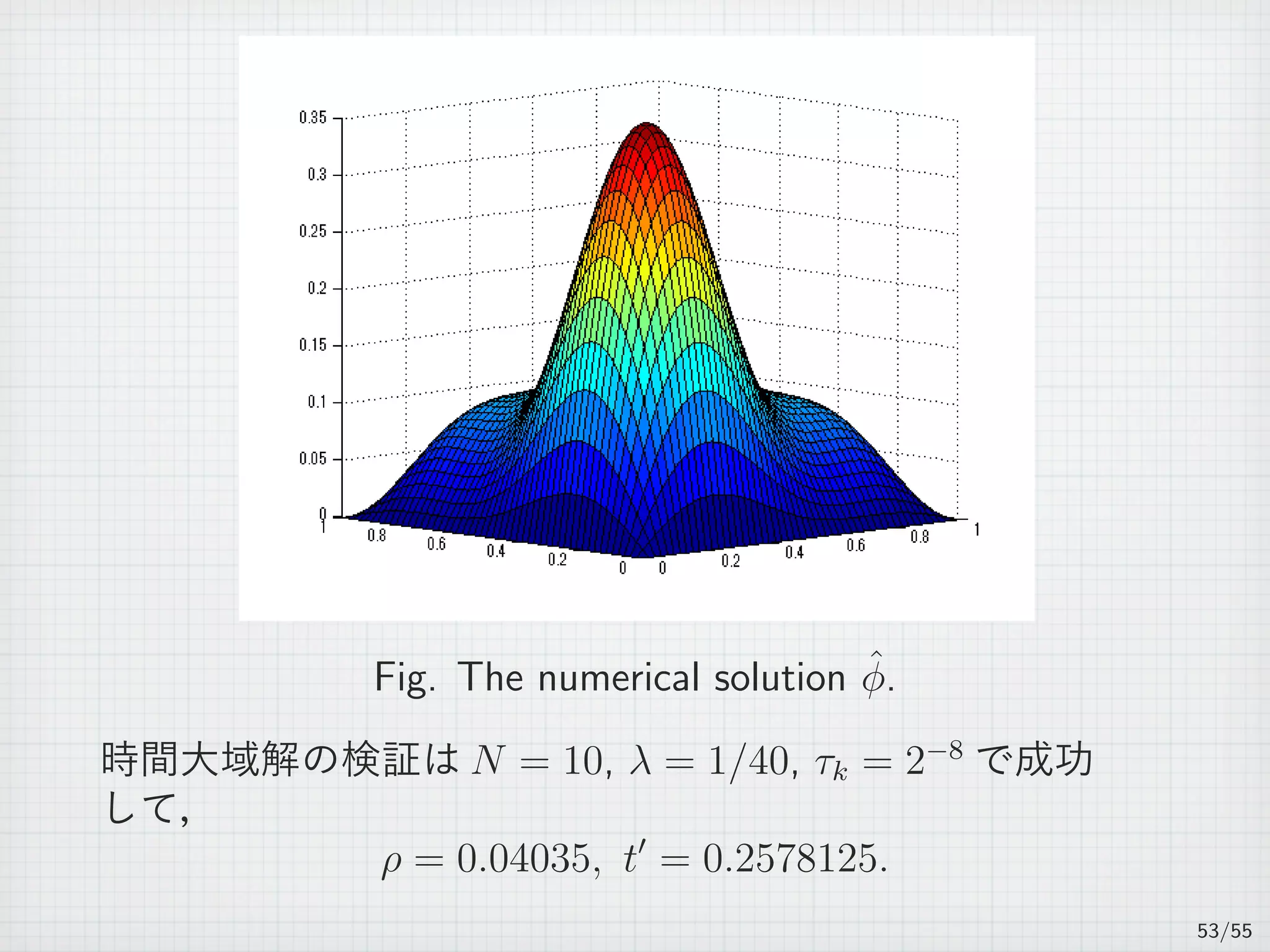
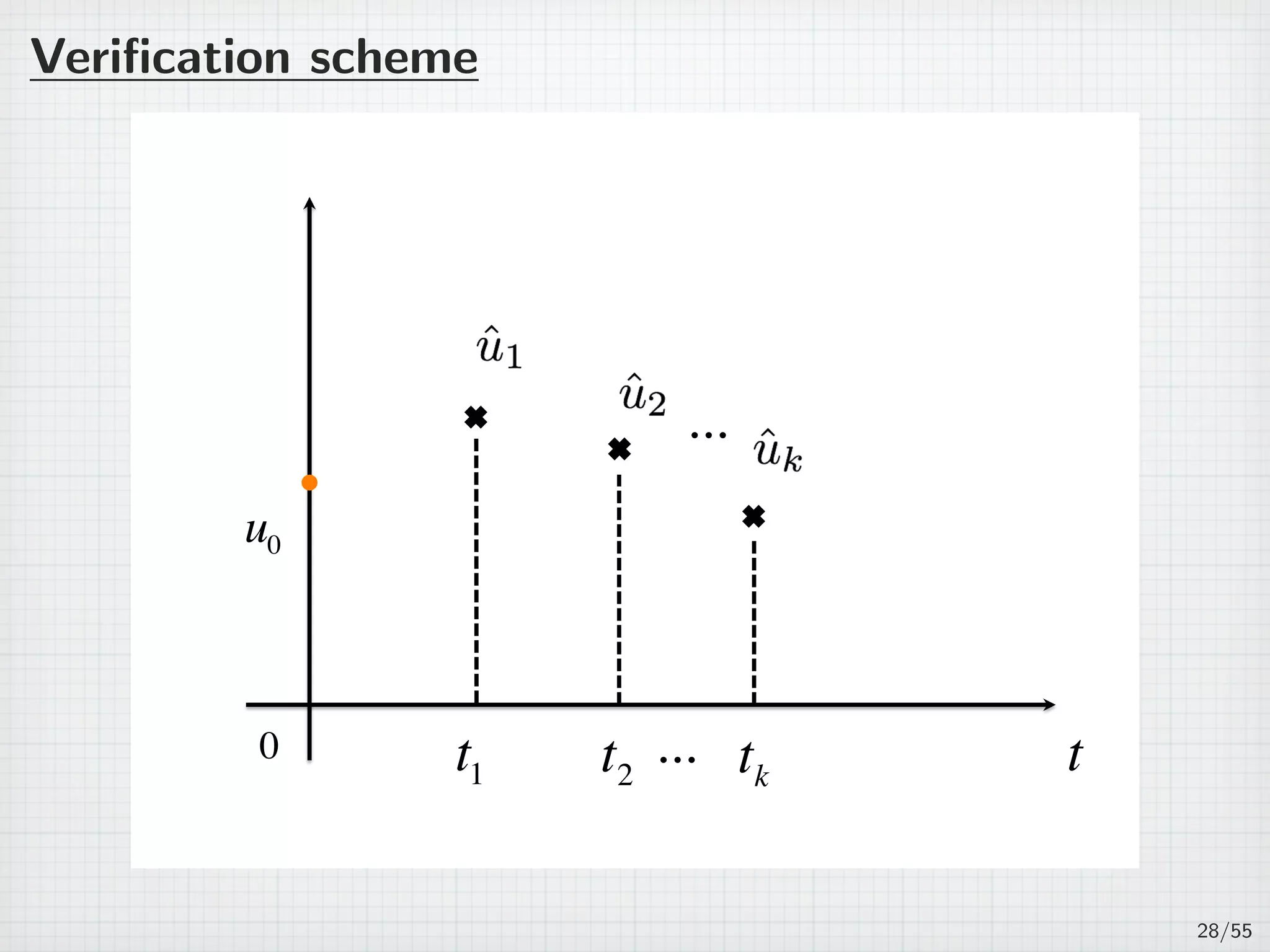
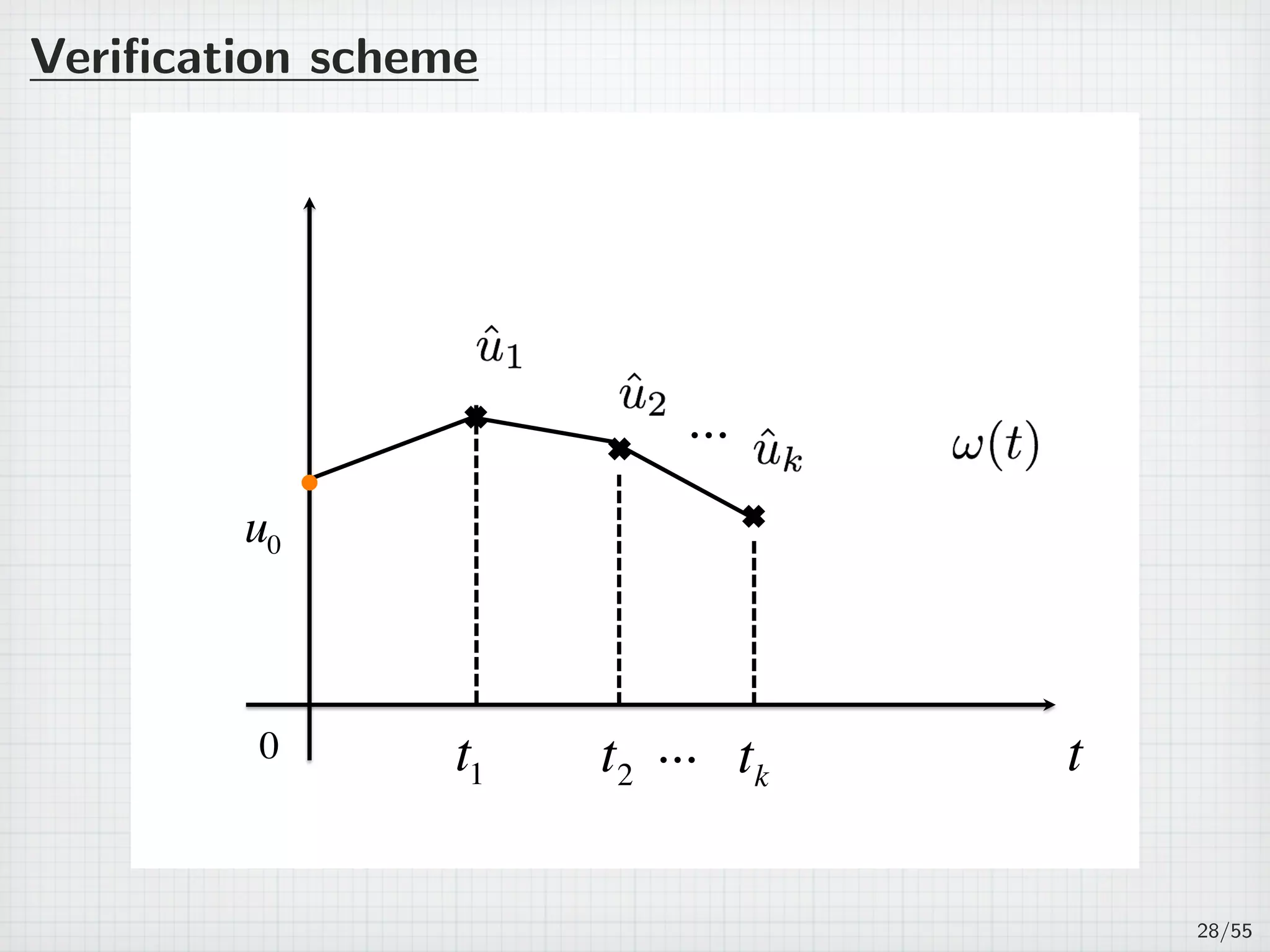
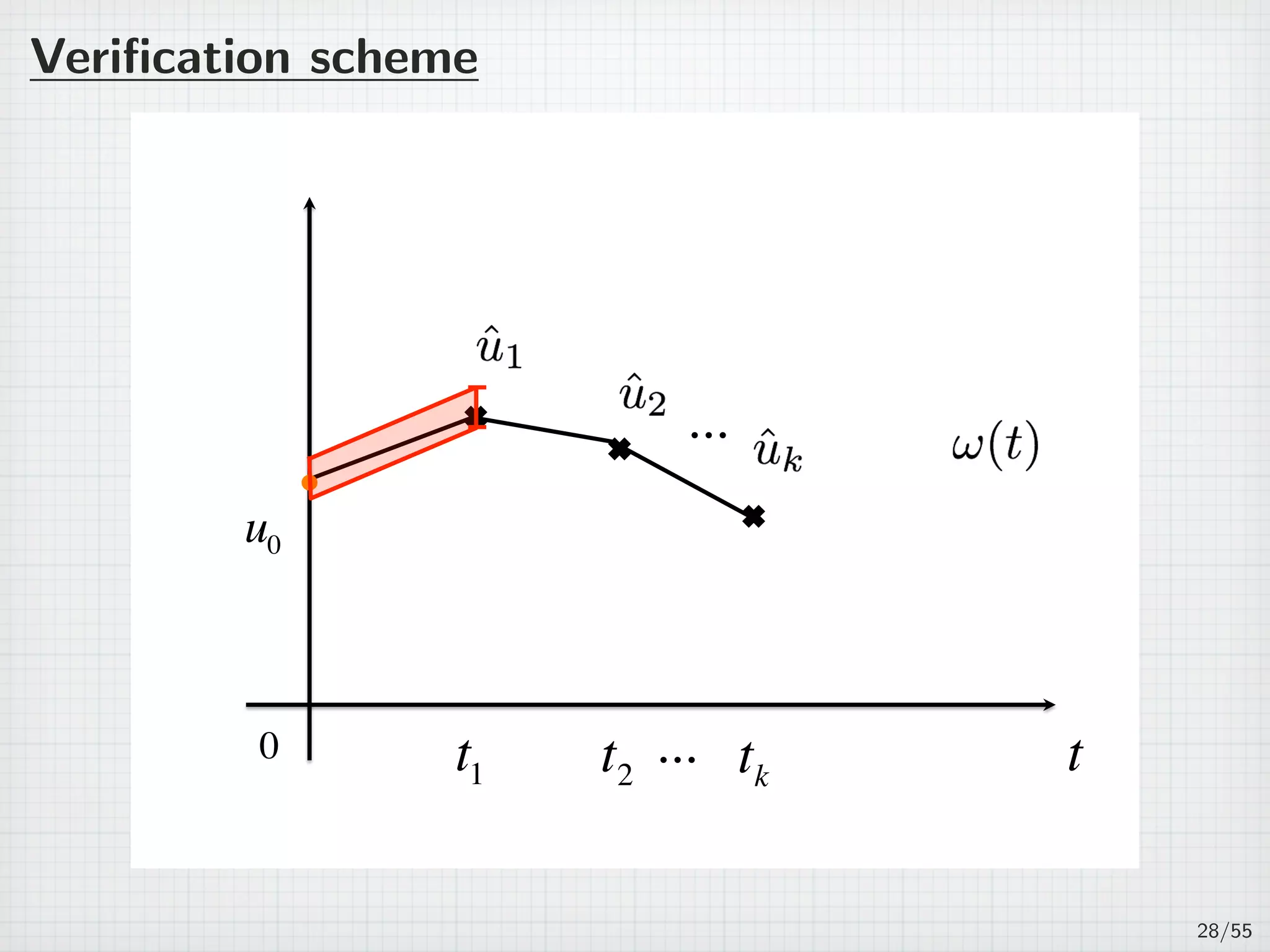
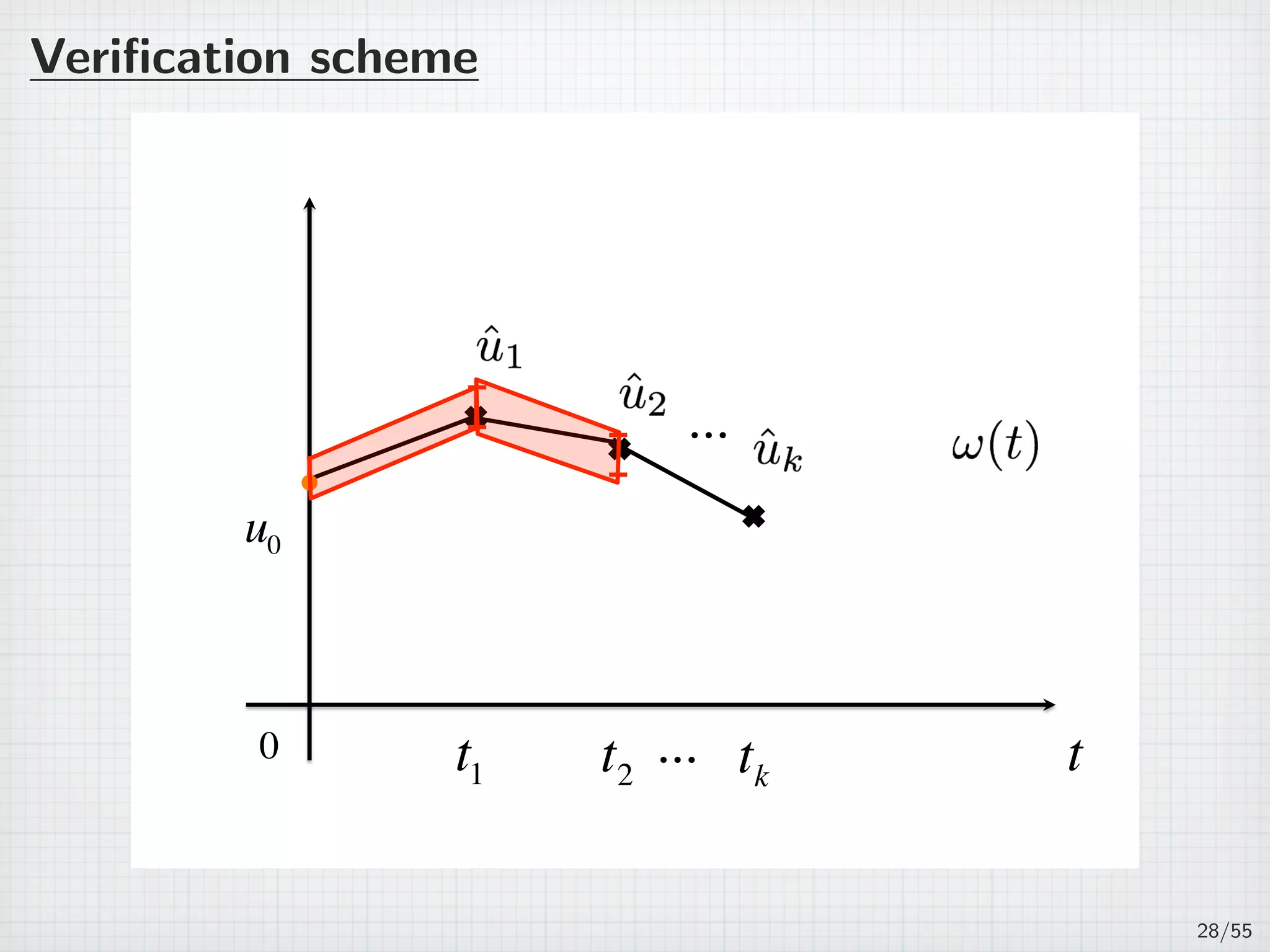
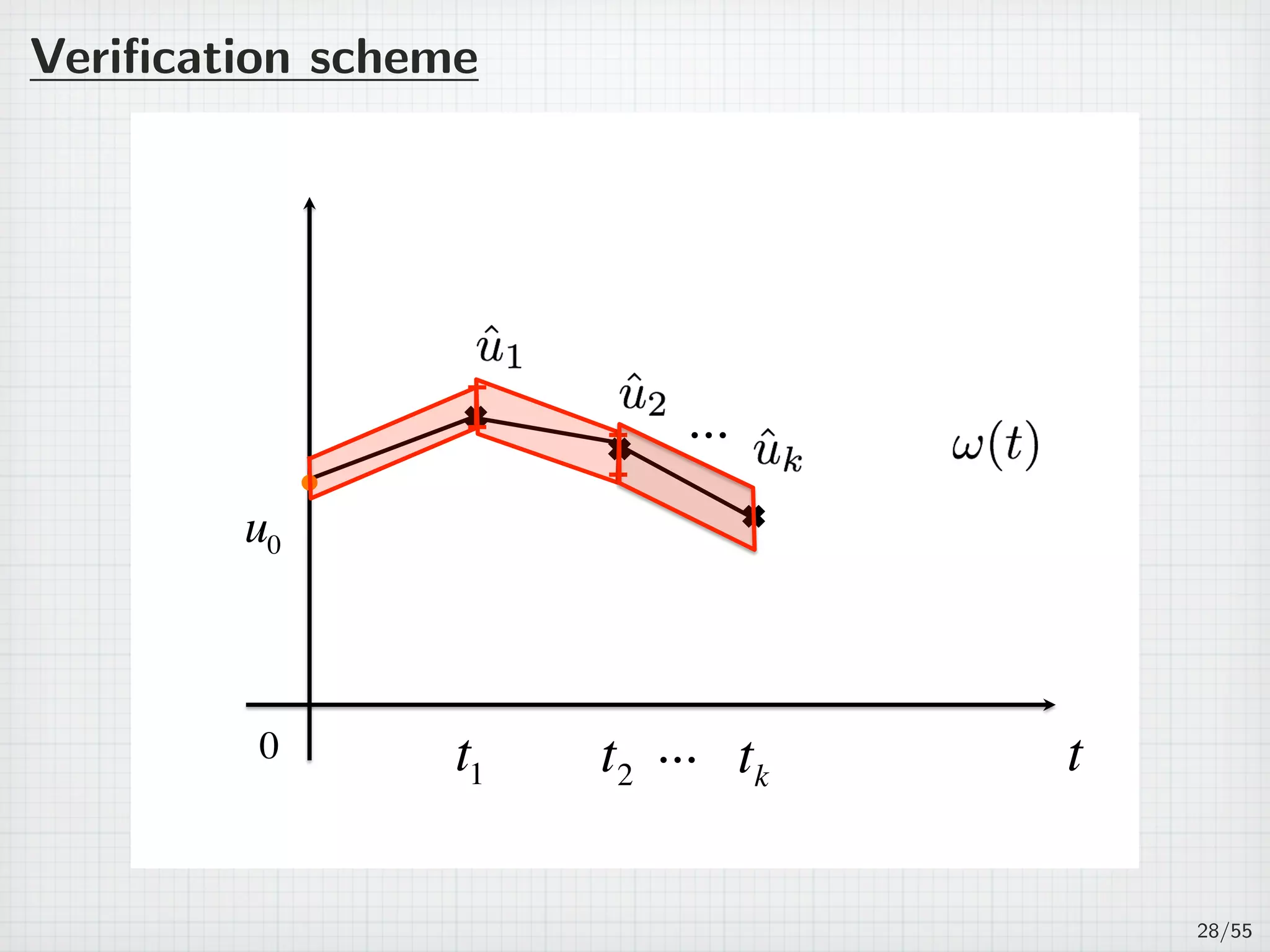
45. On several intervals
For n ∈ N, 0 = t0 t1 · · · tn ∞.
Jk := (tk−1, tk], τk := tk − tk−1, and J =
∪
Jk. (k=1,2,...,n)
(PJ )



∂tu + Au = f(u) in J × Ω,
u(t, x) = 0 on J × ∂Ω,
u(0, x) = u0(x) in Ω,
where u0 ∈ H1
0 (Ω) is a given initial function satisfies
∥u0 − ˆu0∥H1
0
≤ ε0.
26/55

46. Approximate solution (Backward Euler)
Find {uh
k}k≥0 ⊂ Vh such that
(
uh
k − uh
k−1
τ
, vh
)
L2
+ a(uh
k, vh)L2 = (f(uh
k), vh)L2
and
(
uh
0, vh
)
L2 = (u0, vh)L2 for ∀vh ∈ Vh. Numerically
compute each approximation ˆuk (≈ uh
k) ∈ Vh.
From the data ˆuk(≈ uh
k) ∈ Vh, we construct ω(t):
ω(t) :=
n∑
k=0
ˆukϕk(t), t ∈ T,
where ϕk(t) is a piecewise linear Lagrange basis: ϕk(tj) = δkj
(δkj is a Kronecker’s delta).
27/55

47. Approximate solution (Backward Euler)
Find {uh
k}k≥0 ⊂ Vh such that
(
uh
k − uh
k−1
τ
, vh
)
L2
+ a(uh
k, vh)L2 = (f(uh
k), vh)L2
and
(
uh
0, vh
)
L2 = (u0, vh)L2 for ∀vh ∈ Vh. Numerically
compute each approximation ˆuk (≈ uh
k) ∈ Vh.
From the data ˆuk(≈ uh
k) ∈ Vh, we construct ω(t):
ω(t) :=
n∑
k=0
ˆukϕk(t), t ∈ T,
where ϕk(t) is a piecewise linear Lagrange basis: ϕk(tj) = δkj
(δkj is a Kronecker’s delta).
27/55

48. Verification scheme
0 t
u0
t1 t2 tk
...
...
28/55

49. Verification scheme
0 t
u0
t1 t2 tk
...
...
28/55

50. Verification scheme
0 t
u0
t1 t2 tk
...
...
28/55

51. Verification scheme
0 t
u0
t1 t2 tk
...
...
28/55

52. Verification scheme
0 t
u0
t1 t2 tk
...
...
28/55

53. ここまでのまとめ
▶ 各 t ∈ Jk において対象問題
(PJ )



∂tu + Au = f(u) in J × Ω,
u(t, x) = 0 on J × ∂Ω,
u(0, x) = u0(x) in Ω,
に対する弱解の存在と一意性を逐次的に数値解の近傍
BJk
(ω, ρk) に包み込む．
▶ (PJ ) の弱解は各 k = 1, 2, ..., n について
B(ω) :=
{
y ∈ L∞
(
J; H1
0 (Ω)
)
: y(t) ∈ BJk
(ω, ρk), t ∈ Jk
}
の中に一意存在する事が計算機援用証明できる．
29/55

54. ここまでのまとめ
▶ 各 t ∈ Jk において対象問題
(PJ )



∂tu + Au = f(u) in J × Ω,
u(t, x) = 0 on J × ∂Ω,
u(0, x) = u0(x) in Ω,
に対する弱解の存在と一意性を逐次的に数値解の近傍
BJk
(ω, ρk) に包み込む．
▶ (PJ ) の弱解は各 k = 1, 2, ..., n について
B(ω) :=
{
y ∈ L∞
(
J; H1
0 (Ω)
)
: y(t) ∈ BJk
(ω, ρk), t ∈ Jk
}
の中に一意存在する事が計算機援用証明できる．
29/55

55. Computational results 1
30/55

56. 藤田型方程式
Ω = (0, 1)2
: Square domain



∂tu − ∆u = u2
in (0, ∞) × Ω,
u(t, x) = 0 on (0, ∞) × ∂Ω,
u(0, x) = u0 in Ω,
Let γ 0 be an parameter of the initial function:
u0(x) = γx1(1 − x1)x2(1 − x2).
h: spatial mesh size (P2 element),
τ: time step of B.E. method.
31/55

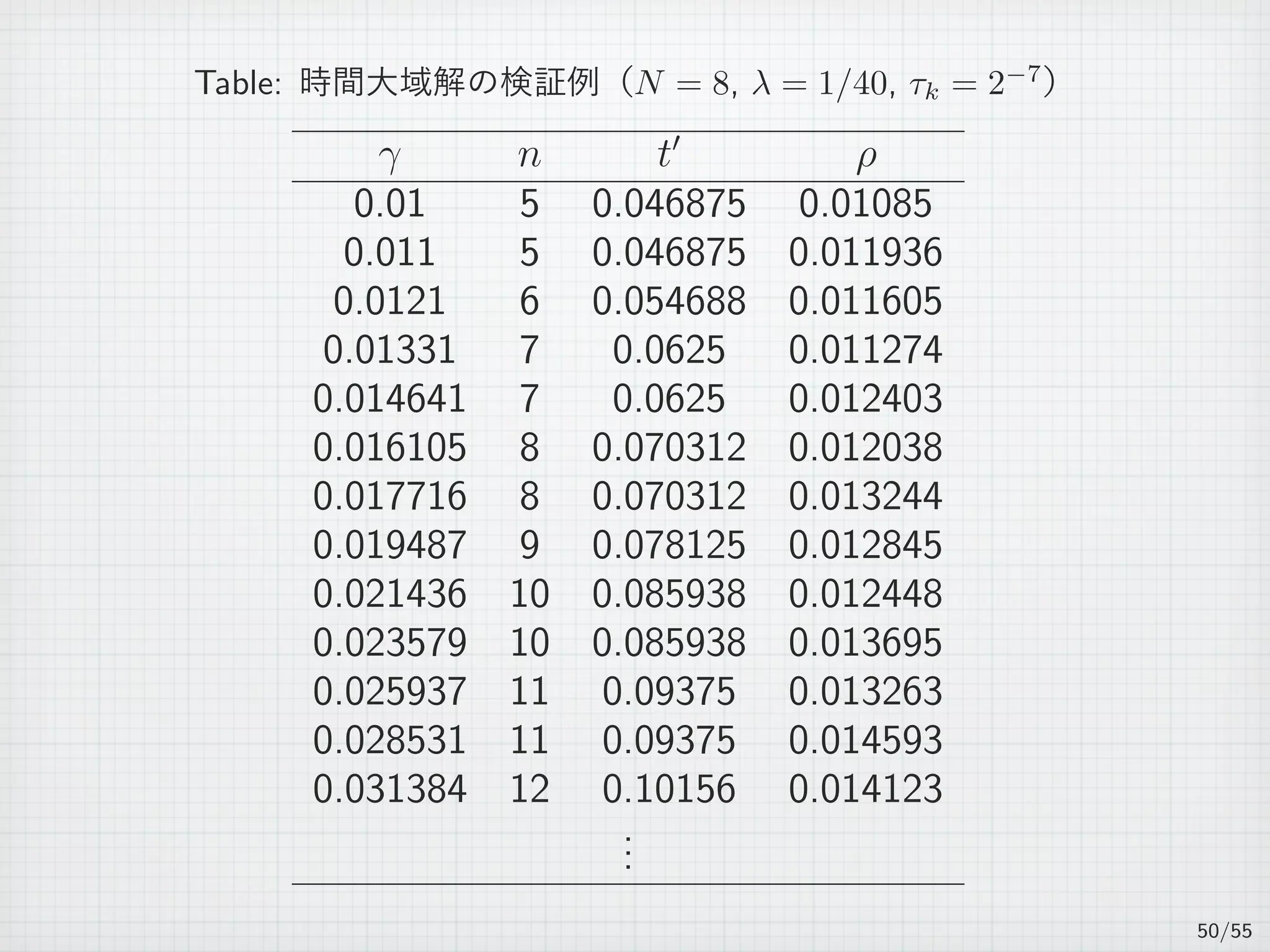
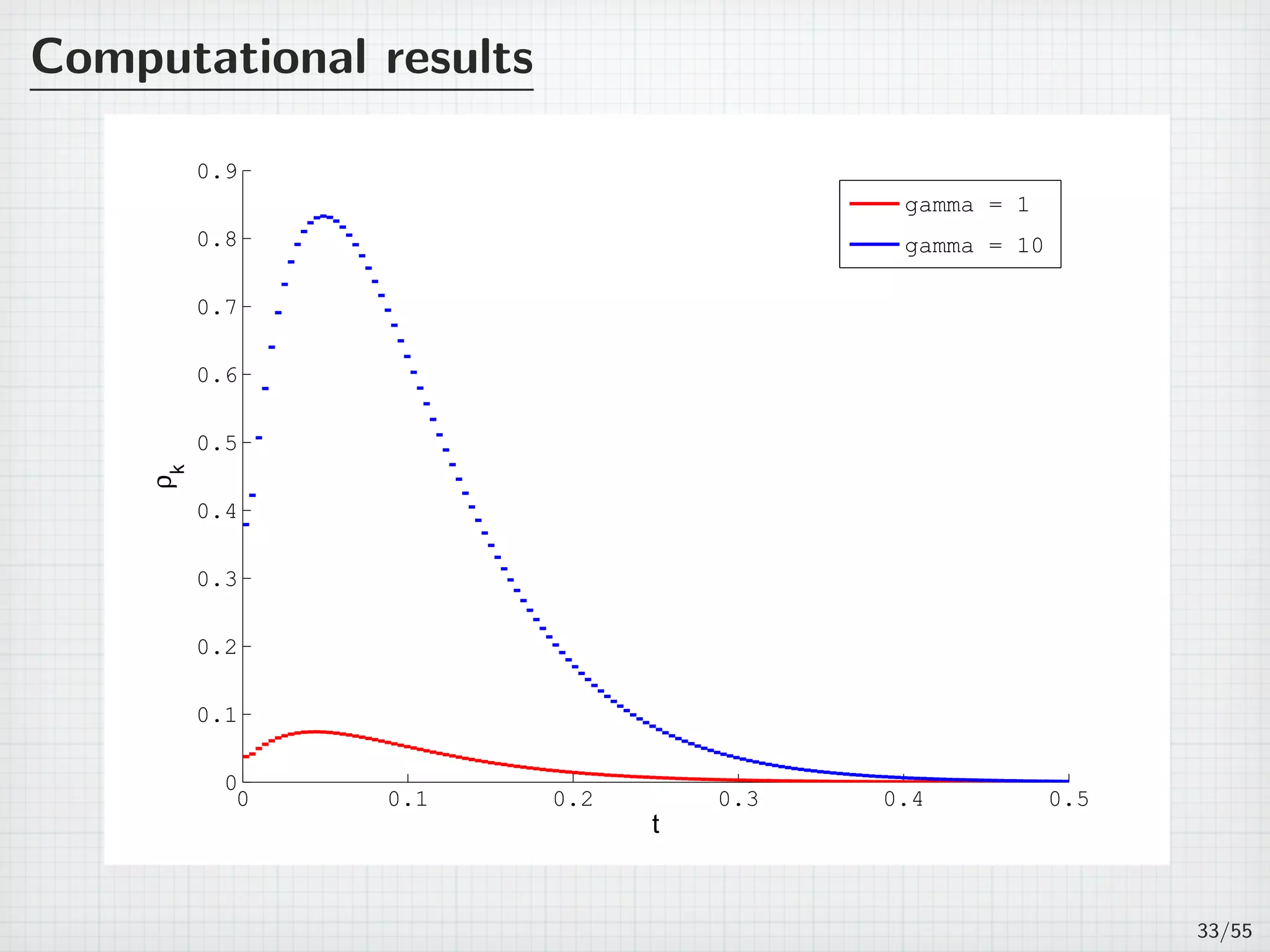
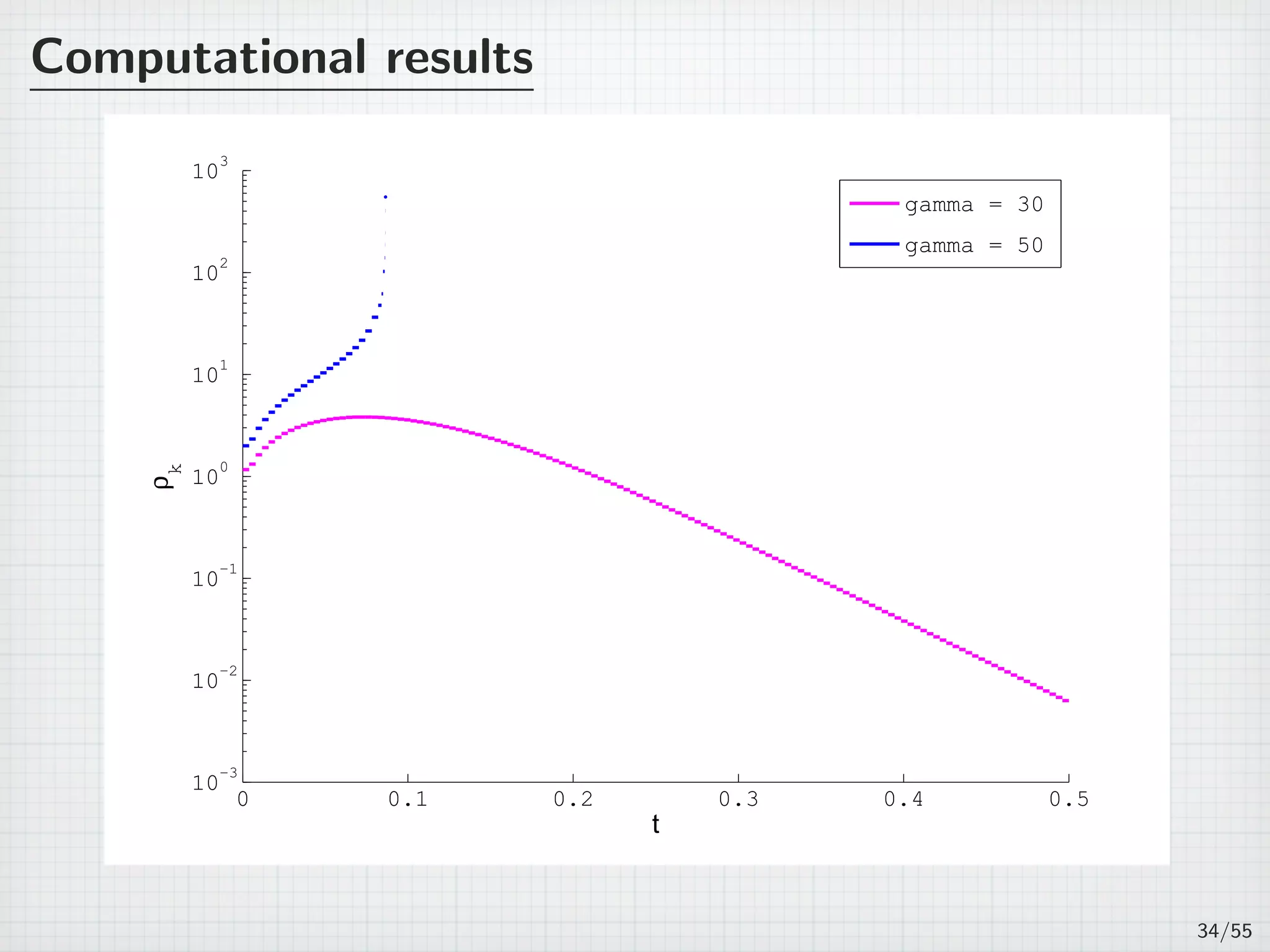
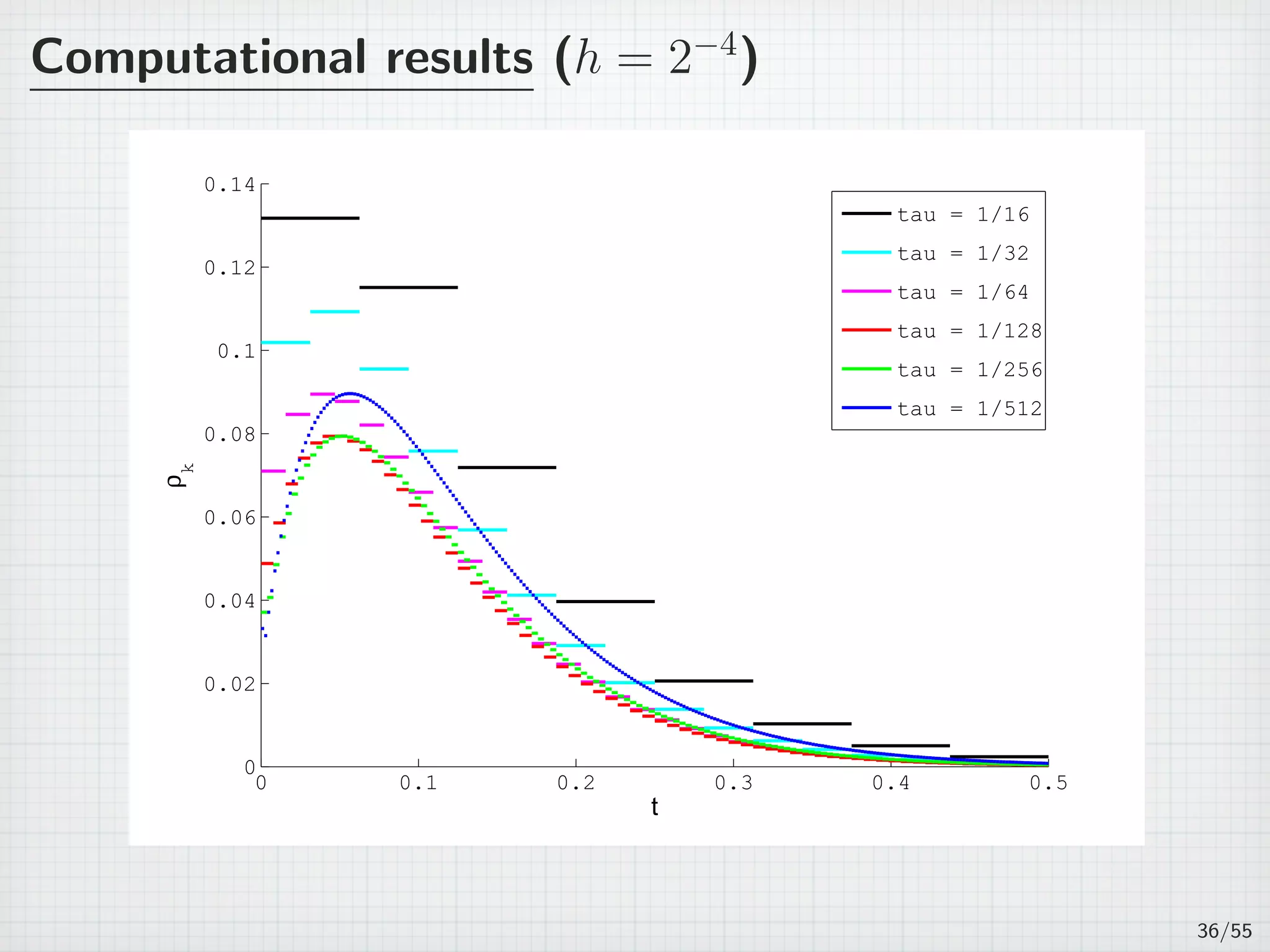
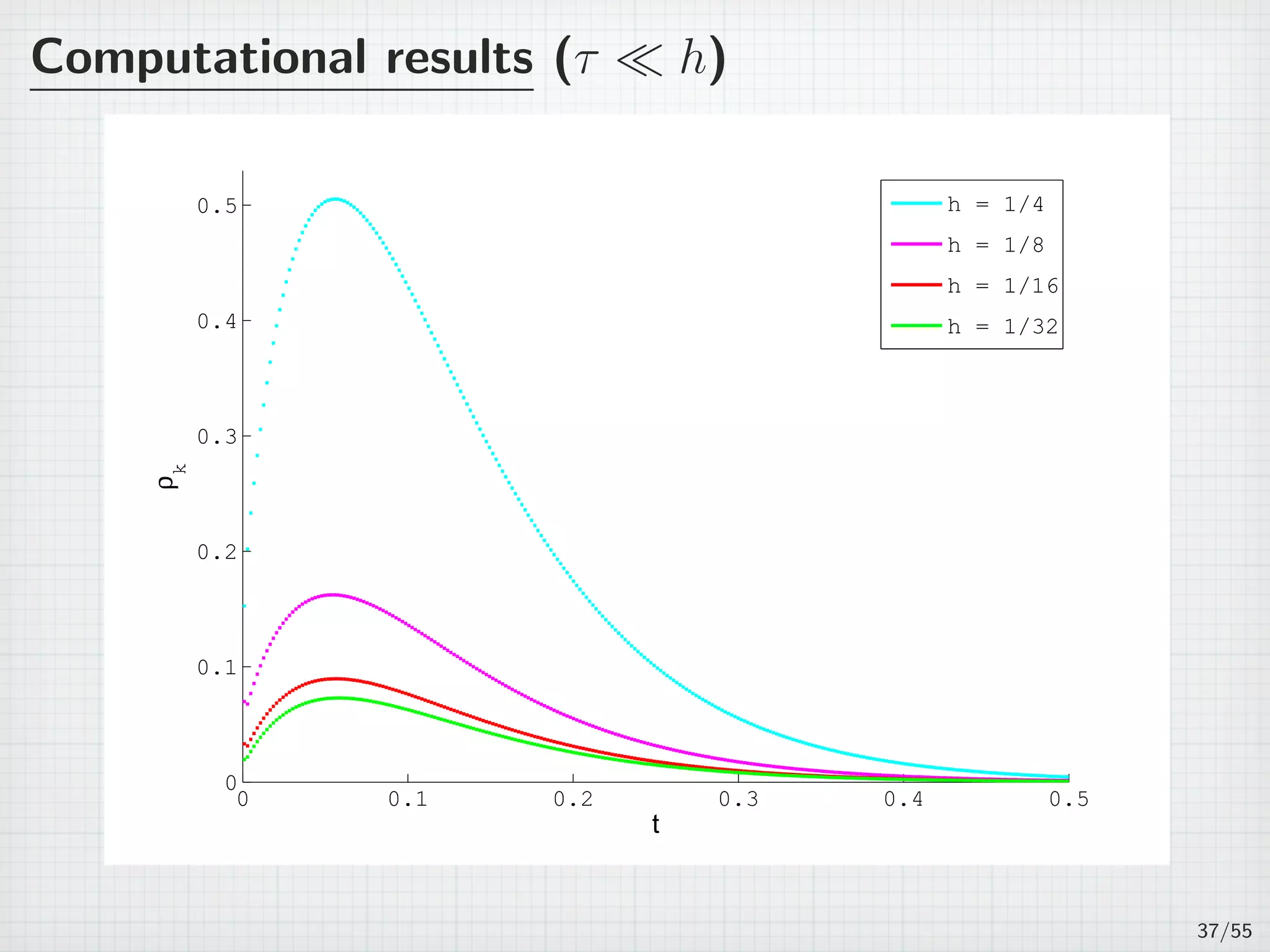
57. Computational results
Table: h = 2−4
, τ = 2−8
, γ = 1.
Tk = (tk−1, tk] εk ρk
(0,0.0039062] 0.020155 0.037646
(0.0039062,0.0078125] 0.030051 0.041554
(0.0078125,0.011719] 0.038089 0.049313
(0.011719,0.015625] 0.044657 0.055699
(0.015625,0.019531] 0.050001 0.060873
...
...
...
(0.48047,0.48438] 0.00013041 0.00014184
(0.48438,0.48828] 0.00012186 0.00013255
(0.48828,0.49219] 0.00011388 0.00012386
(0.49219,0.49609] 0.00010641 0.00011573
(0.49609,0.5] 9.9431E-5 0.00010813
32/55

58. Computational results
0 0.1 0.2 0.3 0.4 0.5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
t
ρk
gamma = 1
gamma = 10
33/55

59. Computational results
0 0.1 0.2 0.3 0.4 0.5
10
−3
10
−2
10
−1
10
0
10
1
10
2
10
3
t
ρ
k
gamma = 30
gamma = 50
34/55

60. 半線形放物型方程式
Ω = (0, 1)2
: Square domain



∂tu − ∆u = u − u3
in (0, ∞) × Ω,
u(t, x) = 0 on (0, ∞) × ∂Ω,
u(0, x) = u0 in Ω.
We set the initial function:
u0(x) = x1(1 − x1)x2(1 − x2).
h: spatial mesh size (P2 element),
τ: time step of B.E. method.
35/55

61. Computational results (h = 2−4
)
0 0.1 0.2 0.3 0.4 0.5
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
t
ρ
k
tau = 1/16
tau = 1/32
tau = 1/64
tau = 1/128
tau = 1/256
tau = 1/512
36/55

62. Computational results (τ ≪ h)
0 0.1 0.2 0.3 0.4 0.5
0
0.1
0.2
0.3
0.4
0.5
t
ρk
h = 1/4
h = 1/8
h = 1/16
h = 1/32
37/55

63. Global existence proof
using verified computations
38/55

64. 時間大域解の証明
本講演では t ∈ (0, ∞) で存在する (PJ ) の解 u(t) ∈ H1
0 (Ω) を
時間大域解といい，以下の 2 つのステップで証明を試みる．
t′
0 をある時刻として
▶ (t′
, ∞) で定常解まわりに大域的に存在する範囲を計算
機で導く．（Global existence proof）
▶ ある時刻 t′
までの解を数値解の近傍に包み込む．
（Concatenation scheme）
上記の方法によって，(PJ ) の時間大域解を関数空間
L∞
(
(0, ∞); H1
0 (Ω)
)
で一意存在することが計算機を用いて証明できる．
39/55

65. 時間大域解の証明
本講演では t ∈ (0, ∞) で存在する (PJ ) の解 u(t) ∈ H1
0 (Ω) を
時間大域解といい，以下の 2 つのステップで証明を試みる．
t′
0 をある時刻として
▶ (t′
, ∞) で定常解まわりに大域的に存在する範囲を計算
機で導く．（Global existence proof）
▶ ある時刻 t′
までの解を数値解の近傍に包み込む．
（Concatenation scheme）
上記の方法によって，(PJ ) の時間大域解を関数空間
L∞
(
(0, ∞); H1
0 (Ω)
)
で一意存在することが計算機を用いて証明できる．
39/55

66. 時間大域解の証明
本講演では t ∈ (0, ∞) で存在する (PJ ) の解 u(t) ∈ H1
0 (Ω) を
時間大域解といい，以下の 2 つのステップで証明を試みる．
t′
0 をある時刻として
▶ (t′
, ∞) で定常解まわりに大域的に存在する範囲を計算
機で導く．（Global existence proof）
▶ ある時刻 t′
までの解を数値解の近傍に包み込む．
（Concatenation scheme）
上記の方法によって，(PJ ) の時間大域解を関数空間
L∞
(
(0, ∞); H1
0 (Ω)
)
で一意存在することが計算機を用いて証明できる．
39/55

67. 大域解の存在に関する先行研究
S. Cai,
“A computer-assisted proof for the pattern formation on
reaction-diffusion systems”, 学位論文, Graduate School of
Mathematics, Kyushu University (2012) 71 pages.
▶ 反応拡散方程式のあるクラスの定常解に対する精度保
証付き数値計算法を示している．
▶ (t′
, ∞) で定常解まわりに大域的に存在する範囲を
L∞
(Ω) × L∞
(Ω) 上で生成された解析半群を用いて，計
算している．
40/55

68. Considered problem
Let Ω be a bounded polygonal domain in R2
and J := (0, ∞).
(PJ )



∂tu + Au = f(u) in J × Ω,
u(t, x) = 0 on J × ∂Ω,
u(0, x) = u0(x) in Ω,
where A = −∆, u0 ∈ H1
0 (Ω) is an initial function, and
f : R → R is a twice Fr´echet differentiable nonlinear mapping.
41/55

69. Considered problem
Let Ω be a bounded polygonal domain in R2
and J := (0, ∞).
(PJ )



∂tu + Au = f(u) in J × Ω,
u(t, x) = 0 on J × ∂Ω,
u(0, x) = u0(x) in Ω,
where A = −∆, u0 ∈ H1
0 (Ω) is an initial function, and
f : R → R is a twice Fr´echet differentiable nonlinear mapping.
41/55

70. Aim of this part
Let Ω be a bounded polygonal domain in R2
.
(PG)



∂tu + Au = f(u) in (t′
, ∞) × Ω,
u(t, x) = 0 on (t′
, ∞) × ∂Ω,
u(t′
, x) = η in Ω,
where η ∈ H1
0 (Ω) satisfies ∥η − ˆun∥H1
0
≤ εn for a certain
εn 0.
We enclose a solution for t ∈ (t′
, ∞) in a neighborhood of a
stationary solution ϕ ∈ D(A) of (PJ ) such that
{
Aϕ = f(ϕ) in Ω,
ϕ = 0 on ∂Ω.
42/55

71. 記号
For ρ 0, v ∈ L∞
((t′
, ∞); H1
0 (Ω)), define a ball
B(v, ρ) :=
{
y ∈ L∞
(
(t′
, ∞); H1
0 (Ω)
)
: ∥y − v∥L∞
((t′,∞);H1
0 (Ω)) ≤ ρ
}
.
The Fr´echet derivative of f at w is denoted by
f′
[w] : L∞
((t′
, ∞); H1
0 (Ω)) → L∞
((t′
, ∞); L2
(Ω)).
For y ∈ B(v, ρ), we assume that there exists a non-decreasing
function L : R → R such that
∥f′
[y]u∥L∞(J;L2(Ω)) ≤ L(ρ)∥u∥H1
0
, u ∈ H1
0 (Ω).
43/55

72. 記号
Define a function space Xλ: for a fixed λ 0,
Xλ :=
{
u ∈ L∞
((t′
, ∞); H1
0 (Ω)) : ess sup
t∈(t′,∞)
e(t−t′)λ
∥u(t)∥H1
0
∞
}
which becomes a Banach space with the norm
∥ · ∥Xλ
:= ess sup
t∈(t′,∞)
e(t−t′)λ
∥u(t)∥H1
0
.
44/55

73. Theorem (Global existence)
Assume that
▶ a solution of (P) is enclosed until t′
0,
▶ a stationary solution ϕ ∈ D(A) uniquely exists around a
numerical solution ˆϕ,
▶ For a ˆun ∈ Vh, εn 0, the initial function satisfies
∥η − ˆun∥H1
0
εn.
For a fixed λ satisfying 0 ≤ λ λmin/2, if ρ 0 satisfies
∥η − ϕ∥H1
0
+ L(ρ)ρ
√
2π
e(λmin − 2λ)
ρ.
Then a solution u(t) for t ∈ (t′
, ∞) uniquely exists in
Uϕ :=
{
u ∈ L∞
(
(t′
, ∞); H1
0 (Ω)
)
: ∥u − ϕ∥Xλ
≤ ρ
}
.
45/55

74. Theorem (Global existence)
Assume that
▶ a solution of (P) is enclosed until t′
0,
▶ a stationary solution ϕ ∈ D(A) uniquely exists around a
numerical solution ˆϕ,
▶ For a ˆun ∈ Vh, εn 0, the initial function satisfies
∥η − ˆun∥H1
0
εn.
For a fixed λ satisfying 0 ≤ λ λmin/2, if ρ 0 satisfies
∥η − ϕ∥H1
0
+ L(ρ)ρ
√
2π
e(λmin − 2λ)
ρ.
Then a solution u(t) for t ∈ (t′
, ∞) uniquely exists in
Uϕ :=
{
u ∈ L∞
(
(t′
, ∞); H1
0 (Ω)
)
: ∥u − ϕ∥Xλ
≤ ρ
}
.
45/55

75. Theorem (Global existence)
Assume that
▶ a solution of (P) is enclosed until t′
0,
▶ a stationary solution ϕ ∈ D(A) uniquely exists around a
numerical solution ˆϕ,
▶ For a ˆun ∈ Vh, εn 0, the initial function satisfies
∥η − ˆun∥H1
0
εn.
For a fixed λ satisfying 0 ≤ λ λmin/2, if ρ 0 satisfies
∥η − ϕ∥H1
0
+ L(ρ)ρ
√
2π
e(λmin − 2λ)
ρ.
Then a solution u(t) for t ∈ (t′
, ∞) uniquely exists in
Uϕ :=
{
u ∈ L∞
(
(t′
, ∞); H1
0 (Ω)
)
: ∥u − ϕ∥Xλ
≤ ρ
}
.
45/55

76. Theorem (Global existence)
Assume that
▶ a solution of (P) is enclosed until t′
0,
▶ a stationary solution ϕ ∈ D(A) uniquely exists around a
numerical solution ˆϕ,
▶ For a ˆun ∈ Vh, εn 0, the initial function satisfies
∥η − ˆun∥H1
0
εn.
For a fixed λ satisfying 0 ≤ λ λmin/2, if ρ 0 satisfies
∥η − ϕ∥H1
0
+ L(ρ)ρ
√
2π
e(λmin − 2λ)
ρ.
Then a solution u(t) for t ∈ (t′
, ∞) uniquely exists in
Uϕ :=
{
u ∈ L∞
(
(t′
, ∞); H1
0 (Ω)
)
: ∥u − ϕ∥Xλ
≤ ρ
}
.
45/55

77. Theorem (Global existence)
Assume that
▶ a solution of (P) is enclosed until t′
0,
▶ a stationary solution ϕ ∈ D(A) uniquely exists around a
numerical solution ˆϕ,
▶ For a ˆun ∈ Vh, εn 0, the initial function satisfies
∥η − ˆun∥H1
0
εn.
For a fixed λ satisfying 0 ≤ λ λmin/2, if ρ 0 satisfies
∥η − ϕ∥H1
0
+ L(ρ)ρ
√
2π
e(λmin − 2λ)
ρ.
Then a solution u(t) for t ∈ (t′
, ∞) uniquely exists in
Uϕ :=
{
u ∈ L∞
(
(t′
, ∞); H1
0 (Ω)
)
: ∥u − ϕ∥Xλ
≤ ρ
}
.
45/55

78. Sketch of proof
Let z ∈ Uϕ. A nonlinear operator
S : L∞
((t′
, ∞); H1
0 (Ω)) → L∞
((t′
, ∞); H1
0 (Ω)) is defined by
S(z) := e−(t−t′)A
(η − ϕ) +
∫ t
t′
e−(t−s)A
(f(z(s)) − f(ϕ)) ds.
On the basis of Banach’s fixed-point theorem, we show a
condition of S having a fixed-point in Uϕ.
For s ∈ (t′
, ∞) and ψ1, ψ2 ∈ Uϕ, the mean-value theorem
states that there exists y ∈ Uϕ such that
∥f(ψ1(s)) − f(ψ2(s))∥L2 = ∥f′
[y(s)](ψ1(s) − ψ2(s))∥L2 .
Since y ∈ Uϕ ⊂ B(ϕ, ρ) holds, we obtain
∥f(ψ1(s)) − f(ψ2(s))∥L2 ≤ L(ρ)∥ψ1(s) − ψ2(s)∥H1
0
.
46/55

79. How to get ∥η − ϕ∥H1
0
?
Since ∥η − ˆun∥H1
0
εn and a stationary solution ϕ encloses in
a neighborhood of a numerical solution, it follows
∥η − ϕ∥H1
0
≤ ∥η − ˆun∥H1
0
+ ∥ˆun − ˆϕ∥H1
0
+ ∥ˆϕ − ϕ∥H1
0
≤ εn + ∥ˆun − ˆϕ∥H1
0
+ ρ′
.
We need to estimate
∥u(t′
) − ˆun∥H1
0
≤ εn.
This can be obtained by the concatenation scheme!
47/55

80. How to get ∥η − ϕ∥H1
0
?
Since ∥η − ˆun∥H1
0
εn and a stationary solution ϕ encloses in
a neighborhood of a numerical solution, it follows
∥η − ϕ∥H1
0
≤ ∥η − ˆun∥H1
0
+ ∥ˆun − ˆϕ∥H1
0
+ ∥ˆϕ − ϕ∥H1
0
≤ εn + ∥ˆun − ˆϕ∥H1
0
+ ρ′
.
We need to estimate
∥u(t′
) − ˆun∥H1
0
≤ εn.
This can be obtained by the concatenation scheme!
47/55

81. How to get ∥η − ϕ∥H1
0
?
Since ∥η − ˆun∥H1
0
εn and a stationary solution ϕ encloses in
a neighborhood of a numerical solution, it follows
∥η − ϕ∥H1
0
≤ ∥η − ˆun∥H1
0
+ ∥ˆun − ˆϕ∥H1
0
+ ∥ˆϕ − ϕ∥H1
0
≤ εn + ∥ˆun − ˆϕ∥H1
0
+ ρ′
.
We need to estimate
∥u(t′
) − ˆun∥H1
0
≤ εn.
This can be obtained by the concatenation scheme!
47/55

82. How to get ∥η − ϕ∥H1
0
?
Since ∥η − ˆun∥H1
0
εn and a stationary solution ϕ encloses in
a neighborhood of a numerical solution, it follows
∥η − ϕ∥H1
0
≤ ∥η − ˆun∥H1
0
+ ∥ˆun − ˆϕ∥H1
0
+ ∥ˆϕ − ϕ∥H1
0
≤ εn + ∥ˆun − ˆϕ∥H1
0
+ ρ′
.
We need to estimate
∥u(t′
) − ˆun∥H1
0
≤ εn.
This can be obtained by the concatenation scheme!
47/55

83. Computational results 2
48/55

84. 藤田型方程式
Let Ω := (0, 1)2
be an unit square domain in R2
.
(F)



∂tu − ∆u = u2
in (0, ∞) × Ω,
u(t, x) = 0 on (0, ∞) × ∂Ω,
u(0, x) = u0(x) in Ω,
where u0(x) = γ sin(πx) sin(πy).
▶ Vh :=
{∑N
k,l=1 ak,l sin(kπx) sin(lπy) : ak,l ∈ R
}
;
▶ Crank-Nicolson scheme is employed;
▶ we fixed λ = 1/40 in the global existence theorem.
49/55

85. Table: 時間大域解の検証例（N = 8, λ = 1/40, τk = 2−7
）
γ n t′
ρ
0.01 5 0.046875 0.01085
0.011 5 0.046875 0.011936
0.0121 6 0.054688 0.011605
0.01331 7 0.0625 0.011274
0.014641 7 0.0625 0.012403
0.016105 8 0.070312 0.012038
0.017716 8 0.070312 0.013244
0.019487 9 0.078125 0.012845
0.021436 10 0.085938 0.012448
0.023579 10 0.085938 0.013695
0.025937 11 0.09375 0.013263
0.028531 11 0.09375 0.014593
0.031384 12 0.10156 0.014123
...
50/55

86. Table: 時間大域解の検証例（N = 8, λ = 1/40, τk = 2−7
）
γ n t′
ρ
...
2.2876 40 0.32031 0.029945
2.5164 41 0.32812 0.0296
2.768 42 0.33594 0.029446
3.0448 42 0.33594 0.034085
3.3493 43 0.34375 0.034657
3.6842 44 0.35156 0.035917
4.0527 45 0.35938 0.038419
4.4579 45 0.35938 0.050511
4.9037 46 0.36719 0.066455
5.3941 47 0.375 0.17656
このとき
∥u(t)∥H1
0
≤ ρe−
(t−t′)
40 , t ∈ (tn, ∞).
51/55

87. 半線形放物型方程式
Let Ω := (0, 1)2
be an unit square domain in R2
.



∂tu − ∆u = f(u) in (0, ∞) × Ω,
u(t, x) = 0 on (0, ∞) × ∂Ω,
u(0, x) = u0(x) in Ω,
where u0(x) = sin(πx) sin(πy).
▶ f(u) = u2
+ 4
∑
1≤k,l≤3 sin(kπx) sin(lπy);
▶ Vh :=
{∑N
k,l=1 ak,l sin(kπx) sin(lπy) : ak,l ∈ R
}
;
▶ Crank-Nicolson scheme is employed;
▶ we fixed λ = 1/40 in the global existence theorem.
52/55

88. Fig. The numerical solution ˆϕ.
時間大域解の検証は N = 10, λ = 1/40, τk = 2−8
で成功
して，
ρ = 0.04035, t′
= 0.2578125.
53/55

89. Fig. The numerical solution ˆϕ.
時間大域解の検証は N = 10, λ = 1/40, τk = 2−8
で成功
して，
ρ = 0.04035, t′
= 0.2578125.
53/55

90. まとめ
▶ 解析半群
{
e−tA
}
t≥0
を用いる精度保証付き数値計算手法
▶ Concatenation scheme（数値解のまわりに包み込む）
▶ 精度保証付き数値計算を用いた時間大域解の存在証明
（定常解のまわりに包み込む）
今後の課題
▶ 方程式の拡張（多種の反応拡散方程式，波動方程式等）
▶ 無限次元力学系との関連
▶ 藤田型方程式の爆発時刻の精度保証付き数値計算
54/55

91. Thank you for kind attention!
55/55