This document contains a multi-part exam question regarding dynamic control systems. It asks the student to perform block diagram reductions to solve for various transfer functions T(s). It also asks the student to analyze the system poles, find damping ratio and natural frequency, and determine the unit impulse and step responses. Additional questions involve analyzing the characteristics of a flow system and determining sensitivity functions.

1. Page1/9
DYNAMIC CONTROL SYSTEMS
(SBE_305A)
Final Exam
Spring 2015
Cairo University
Faculty of Engineering
Systemsand Biomedical Engineering Dept.
Answer ONLY FIVE Questions (Full Mark 75 points)____ Time Allowed : 3 Hours
Question 1 (15 points):
a) Using block diagram reduction:
Now 𝑮 𝟒(𝒔) =
𝑮 𝟑(𝒔)
𝟏+𝑮 𝟑(𝒔)𝑯 𝟑(𝒔)
𝑮 𝟓(𝒔) =
𝟏
𝑮 𝟐(𝒔)
𝑮 𝟔(𝒔) =
𝑮 𝟐(𝒔)
𝟏+𝑮 𝟐(𝒔)𝑯 𝟐(𝒔)
𝑮 𝟕(𝒔) =
𝑮 𝟏(𝒔)𝑮 𝟔(𝒔)
𝟏+𝑮 𝟏(𝒔)𝑮 𝟔(𝒔)𝑯 𝟏(𝒔)
=
𝑮 𝟏(𝒔)∙
𝑮 𝟐(𝒔)
𝟏+𝑮 𝟐(𝒔)𝑯 𝟐(𝒔)
𝟏+𝑮 𝟏(𝒔)∙
𝑮 𝟐(𝒔)
𝟏+𝑮 𝟐(𝒔)𝑯 𝟐(𝒔)
∙𝑯 𝟏(𝒔)
=
𝑮 𝟏(𝒔)𝑮 𝟐(𝒔)
𝟏+𝑮 𝟐(𝒔)𝑯 𝟐(𝒔)+𝑮 𝟏(𝒔)𝑮 𝟐(𝒔)𝑯 𝟏(𝒔)
=
𝑮 𝟏(𝒔)𝑮 𝟐(𝒔)
𝟏+𝑮 𝟐(𝒔)[𝑯 𝟐(𝒔)+𝑮 𝟏(𝒔)𝑯 𝟏(𝒔)]
𝑮 𝟖(𝒔) = 𝟏 + 𝑮 𝟓(𝒔) = 𝟏 +
𝟏
𝑮 𝟐(𝒔)
=
𝟏 + 𝑮 𝟐(𝒔)
𝑮 𝟐(𝒔)
∴ 𝑻(𝒔) =
𝑪(𝒔)
𝑹(𝒔)
= 𝑮 𝟕(𝒔)𝑮 𝟖(𝒔)𝑮 𝟒(𝒔) =
𝑮 𝟏(𝒔)𝑮 𝟐(𝒔)
𝟏 + 𝑮 𝟐(𝒔)[𝑯 𝟐(𝒔) + 𝑮 𝟏(𝒔)𝑯 𝟏(𝒔)]
𝟏 + 𝑮 𝟐(𝒔)
𝑮 𝟐(𝒔)
𝑮 𝟑(𝒔)
𝟏 + 𝑮 𝟑(𝒔)𝑯 𝟑(𝒔)
R(s) C(s)
G1(s) G2(s) G4(s)
H2(s)
H1(s)
+ + +
+--
G1(s) G2(s) G4(s)
G5(s)
H1(s)
H2(s)
R(s) C(s)
G5(s)
G1(s) G6(s) G4(s)
H1(s)
R(s) C(s)
G7(s)
G5(s)
G4(s)
R(s)
C(s)
G7(s) G8(s) (s)4G
R(s)
C(s)

2. Page2/9
=
𝑮 𝟏(𝒔)𝑮 𝟑(𝒔)[𝟏 + 𝑮 𝟐(𝒔)]
[𝟏 + 𝑮 𝟑(𝒔)𝑯 𝟑(𝒔)]{𝟏 + 𝑮 𝟐(𝒔)[𝑯 𝟐(𝒔) + 𝑮 𝟏(𝒔)𝑯 𝟏(𝒔)]}
𝑻(𝒔) =
𝑪(𝒔)
𝑹(𝒔)
=
∑ 𝑷 𝒊∆𝒊
∆
=
𝑷 𝟏∆ 𝟏+𝑷 𝟐∆ 𝟐
∆
𝑷 𝟏 = 𝒔 𝑷 𝟐 =
𝟏
𝒔 𝟐
𝑳 𝟏 = 𝑳 𝟑 = −𝒔 𝟐
𝑳 𝟐 = 𝑳 𝟒 = −
𝟏
𝒔
∴ ∆= 𝟏 − (𝑳 𝟏 + 𝑳 𝟐 + 𝑳 𝟑 + 𝑳 𝟒) = 𝟏 + (𝒔 𝟐
+
𝟏
𝒔
+ 𝒔 𝟐
+
𝟏
𝒔
) = 𝟏 +
𝟐𝒔 𝟑
+ 𝟐
𝒔
=
𝟐𝒔 𝟑
+ 𝒔 + 𝟐
𝒔
∴ 𝑻(𝒔) = (𝒔 +
𝟏
𝒔 𝟐
) ∙
𝒔
𝟐𝒔 𝟑 + 𝒔 + 𝟐
=
𝒔(𝒔 𝟑
+ 𝟏)
𝒔 𝟐(𝟐𝒔 𝟑 + 𝒔 + 𝟐)
=
𝒔 𝟑
+ 𝟏
𝒔(𝟐𝒔 𝟑 + 𝒔 + 𝟐)
c) Let 𝑮 𝟏(𝒔) = 𝒔 𝟐
𝑮 𝟐(𝒔) =
𝟏
𝒔
𝑮 𝟑(𝒔) = 𝑮 𝟏(𝒔) + 𝑮 𝟐(𝒔)
𝑮 𝟒(𝒔) = 𝒇𝒆𝒆𝒅𝒃𝒂𝒄𝒌(𝑮 𝟑(𝒔), 𝟏)
𝑮 𝟓(𝒔) = 𝑮 𝟒(𝒔) ∙
𝟏
𝒔
𝑻(𝒔) = 𝒇𝒆𝒆𝒅𝒃𝒂𝒄𝒌(𝑮 𝟑(𝒔), 𝟏)
Thus, the Matlab code is given by:

3. Page3/9
>>num1=[1 0 0]
>>den1=[1]
>>G1=tf(num1,den1)
>>num2=[1]
>>den1=[1 0]
>>G2=tf(num2,den2)
>>G3=G1+G2
>>G4=feedback(G3,[1])
>>G5= G4*G2
>>num6=[1 0]
>>den6=[1]
>>G6=tf(num6,den6)
>>T=feedback(G5,G6)
Question 2 (15 points):
a) The system poles are given by: s = -10, s = -3 ± j
b) The damping ratio and natural frequency of the dominant poles can be obtained by equating the
second factor of the denominator with zero. This takes the form:
𝒔 𝟐
+ 𝟐𝜻𝝎 𝒏 + 𝝎 𝒏
𝟐
= 𝟎
∴ 𝟐𝜻𝝎 𝒏 = 𝟔 ===> 𝜻𝝎 𝒏 = 𝟑
𝝎 𝒏
𝟐
= 𝟏𝟎 ===> 𝝎 𝒏 = √𝟏𝟎 𝒓𝒂𝒅/𝒔
∴ 𝜻√𝟏𝟎 = 𝟑 ===> 𝜻 =
𝟑
√𝟏𝟎
= 𝟎. 𝟗𝟒𝟗
c) For the unit impulse response R(s) = 1. Thus
𝒀(𝒔) =
𝟓𝒔 + 𝟏
(𝒔 + 𝟏𝟎)(𝒔 𝟐 + 𝟔𝒔 + 𝟏𝟎)
=
𝟒𝟗𝒔 + 𝟓𝟒
𝟓𝟎(𝒔 𝟐 + 𝟔𝒔 + 𝟏𝟎)
−
𝟒𝟗
𝟓𝟎(𝒔 + 𝟏𝟎)
=
𝟒𝟗(𝒔 + 𝟑) − 𝟗𝟑
𝟓𝟎[(𝒔 + 𝟑) 𝟐 + 𝟏]
−
𝟒𝟗
𝟓𝟎(𝒔 + 𝟏𝟎)
∴ 𝒚(𝒕) = 𝟎. 𝟗𝟖𝒆−𝟑𝒕
∙ 𝐜𝐨𝐬 𝒕 − 𝟏. 𝟖𝟔𝒆−𝟑𝒕
∙ 𝐬𝐢𝐧 𝒕 − 𝟎. 𝟗𝟖𝒆−𝟏𝟎𝒕
= 𝟐. 𝟏𝟎𝟐𝟑𝟖𝒆−𝟑𝒕
∙ 𝐜𝐨𝐬(𝒕 + 𝟔𝟐. 𝟐°) − 𝟎. 𝟗𝟖𝒆−𝟏𝟎𝒕
d) For the unit step response 𝑹(𝒔) =
𝟏
𝐬
. Thus
𝒀(𝒔) =
𝟓𝒔 + 𝟏
𝒔(𝒔 + 𝟏𝟎)(𝒔 𝟐 + 𝟔𝒔 + 𝟏𝟎)
=
𝟏
𝟏𝟎𝟎𝒔
+
𝟒𝟗
𝟓𝟎𝟎(𝒔 + 𝟏𝟎)
+
𝟖𝟑 − 𝟐𝟕𝒔
𝟐𝟓𝟎(𝒔 𝟐 + 𝟔𝒔 + 𝟏𝟎)
=
𝟏
𝟏𝟎𝟎𝒔
+
𝟒𝟗
𝟓𝟎𝟎(𝒔 + 𝟏𝟎)
−
𝟐𝟕(𝒔 + 𝟑) − 𝟏𝟔𝟒
𝟐𝟓𝟎[(𝒔 + 𝟑) 𝟐 + 𝟏]
∴ 𝒚(𝒕) = 𝟎. 𝟎𝟏 + 𝟎. 𝟎𝟗𝟖𝒆−𝟏𝟎𝒕
− 𝟎. 𝟏𝟎𝟖𝒆−𝟑𝒕
∙ 𝐜𝐨𝐬 𝒕 + 𝟎. 𝟔𝟓𝟔𝒆−𝟑𝒕
∙ 𝐬𝐢𝐧 𝒕
= 𝟎. 𝟎𝟏 + 𝟎. 𝟎𝟗𝟖𝒆−𝟏𝟎𝒕
− 𝟎. 𝟔𝟔𝟒𝟖𝟑𝒆−𝟑𝒕
∙ 𝐜𝐨𝐬(𝒕 + 𝟖𝟎. 𝟕°)
e) ess(∞) = 1 – T(0) = 𝟏 −
𝟏
𝟏𝟎×𝟏𝟎
= 𝟎. 𝟗𝟗 = 𝟗𝟗%

4. Page4/9
Question 3 (15 points):
a) Let the driving pressure be given by Pd = P1 – P2
∴ 𝑸 = 𝑲√𝑷 𝒅
∴ ∆𝑸 =
𝒅𝑸
𝒅𝑷 𝒅
∆𝑷 𝒅 =
𝑲
𝟐√𝑷 𝒅
∆𝑷 𝒅 =
𝑲
𝟐√𝑷 𝟏 − 𝑷 𝟐
∆(𝑷 𝟏 − 𝑷 𝟐)
Now if Pd = P1 – P2 = 0, then in that limiting case the slope of the Q – (P1 – P2) characteristic
approaches infinity. So, for an infinitesimal change in P1 – P2 the change in Q grows beyond all
limits.
b) 𝑺 𝑮
𝑻
=
𝟏
𝟏+𝑮(𝒔)𝑯(𝒔)
=
𝟏
𝟏+𝑮(𝒔)
=
𝟏
𝟏+
𝟒𝟎𝟎
𝒔 𝟐+𝟖𝒔+𝟒𝟎𝟎
=
𝒔 𝟐+𝟖𝒔+𝟒𝟎𝟎
𝒔 𝟐+𝟖𝒔+𝟖𝟎𝟎
𝑺 𝑯
𝑻
=
− 𝑮( 𝒔) 𝑯(𝒔)
𝟏 + 𝑮( 𝒔) 𝑯(𝒔)
= −
𝟒𝟎𝟎 × 𝟏
𝒔 𝟐 + 𝟖𝒔 + 𝟒𝟎𝟎
∙
𝒔 𝟐 + 𝟖𝒔 + 𝟒𝟎𝟎
𝒔 𝟐 + 𝟖𝒔 + 𝟖𝟎𝟎
= −
𝟒𝟎𝟎
𝒔 𝟐 + 𝟖𝒔 + 𝟖𝟎𝟎
c) 𝑺 𝑮
𝑻
=
𝟏
𝟏+𝑮(𝒔)𝑯(𝒔)
=
𝟏
𝟏+
𝟒𝟎𝟎
𝒔 𝟐+𝟖𝒔+𝟒𝟎𝟎
∙
𝟏
𝒔
=
𝒔( 𝒔 𝟐
+𝟖𝒔+𝟒𝟎𝟎)
𝒔( 𝒔 𝟐+𝟖𝒔+𝟒𝟎𝟎)+𝟒𝟎𝟎
=
𝒔 𝟑
+𝟖𝒔 𝟐
+𝟒𝟎𝟎𝒔
𝒔 𝟑+𝟖𝒔 𝟐+𝟒𝟎𝟎𝒔+𝟒𝟎𝟎
𝑺 𝑯
𝑻
=
− 𝑮( 𝒔) 𝑯(𝒔)
𝟏+𝑮( 𝒔) 𝑯(𝒔)
= − 𝟒𝟎𝟎
𝒔 𝟐+𝟖𝒔+𝟒𝟎𝟎
∙ 𝟏
𝒔
∙ 𝒔 𝟑+𝟖𝒔 𝟐+𝟒𝟎𝟎𝒔
𝒔 𝟑+𝟖𝒔 𝟐+𝟒𝟎𝟎𝒔+𝟒𝟎𝟎
= −𝟒𝟎𝟎
𝒔 𝟑+𝟖𝒔 𝟐+𝟒𝟎𝟎𝒔+𝟒𝟎𝟎
d) The circuit becomes
Y1(s) = R1·I(s)
𝑰(𝒔) =
𝑼 𝟏(𝒔)
𝒁(𝒔)
Z(s)= Z1(s)+ Z2(s)
Z1(s)= R1+sL1

5. Page5/9
𝒁 𝟐(𝒔) =
𝑹 𝟐(𝑹 𝟑+
𝟏
𝒔𝑪
)
𝑹 𝟐+𝑹 𝟑+
𝟏
𝒔𝑪
=
𝑹 𝟐(𝒔𝑪𝑹 𝟑+𝟏)
𝒔𝑪(𝑹 𝟐+𝑹 𝟑)+𝟏
∴ 𝒁(𝒔) = 𝑹 𝟏 + 𝒔𝑳 𝟏 +
𝑹 𝟐( 𝒔𝑪𝑹 𝟑 + 𝟏)
𝒔𝑪( 𝑹 𝟐 + 𝑹 𝟑) + 𝟏
=
[ 𝒔𝑪( 𝑹 𝟐 + 𝑹 𝟑) + 𝟏](𝑹 𝟏 + 𝒔𝑳 𝟏) + 𝑹 𝟐( 𝒔𝑪𝑹 𝟑 + 𝟏)
𝒔𝑪( 𝑹 𝟐 + 𝑹 𝟑) + 𝟏
=
𝒔 𝟐
𝑪𝑳 𝟏(𝑹 𝟐 + 𝑹 𝟑) + 𝒔[𝑪(𝑹 𝟐 + 𝑹 𝟑)𝑹 𝟏 + 𝑳 𝟏 + 𝑪𝑹 𝟐 𝑹 𝟑] + (𝑹 𝟏 + 𝑹 𝟐)
𝒔𝑪(𝑹 𝟐 + 𝑹 𝟑) + 𝟏
∴ 𝑰(𝒔)
=
𝒔𝑪(𝑹 𝟐 + 𝑹 𝟑) + 𝟏
𝒔 𝟐 𝑪𝑳 𝟏(𝑹 𝟐 + 𝑹 𝟑) + 𝒔[𝑪(𝑹 𝟐 + 𝑹 𝟑)𝑹 𝟏 + 𝑳 𝟏 + 𝑪𝑹 𝟐 𝑹 𝟑] + (𝑹 𝟏 + 𝑹 𝟐)
𝑼 𝟏(𝒔)
∴
𝒀 𝟏(𝒔)
𝑼 𝟏(𝒔)
=
𝑹 𝟏[𝒔𝑪(𝑹 𝟐 + 𝑹 𝟑) + 𝟏]
𝒔 𝟐 𝑪𝑳 𝟏(𝑹 𝟐 + 𝑹 𝟑) + 𝒔[𝑪(𝑹 𝟐 + 𝑹 𝟑)𝑹 𝟏 + 𝑳 𝟏 + 𝑪𝑹 𝟐 𝑹 𝟑] + (𝑹 𝟏 + 𝑹 𝟐)
Question 4 (15 points):
a) We can obtain the state space model from the transfer function as follows:
U(s) +
Let 𝐺2(𝑠) = 𝐺1(𝑠) ∙
1
𝑠
Now 𝐺1(𝑠) = 𝑎 +
𝑏
𝑠
=
𝑎𝑠+𝑏
𝑠
∴ 𝐺2(𝑠) =
𝑎𝑠 + 𝑏
𝑠2
∴ 𝐺(𝑠) =
𝑌(𝑠)
𝑈(𝑠)
=
𝐺2(𝑠)
1 + 𝐺2(𝑠)
=
𝑎𝑠+𝑏
𝑠2
1 +
𝑎𝑠+𝑏
𝑠2
=
𝑎𝑠 + 𝑏
𝑠2 + 𝑎𝑠 + 𝑏
This is of the form
𝐺(𝑠) =
𝑏 𝑜 𝑠2
+ 𝑏1 𝑠 + 𝑏2
𝑠2 + 𝑎1 𝑠 + 𝑎2
In that case the state model is given by:
𝐀 = [
0 1
−𝑎2 −𝑎1
] = [
0 1
−𝑏 −𝑎
]
G1(s)
𝟏
𝒔
_
Y(s)

6. Page6/9
𝐁 = 𝜷 = [
𝛽1
𝛽2
] = 𝐛 − 𝐋𝛃′
= [
𝑏1
𝑏2
] − [
𝑎1 0
𝑎2 𝑎1
] [
𝑏 𝑜
𝛽1
]
𝐂 = [1 0] 𝐃 = 𝑏 𝑜 = 0
𝛽1 = 𝑏1 − 𝑎1 𝑏 𝑜 = 𝑎
𝛽2 = 𝑏2 − 𝑎2 𝑏 𝑜 − 𝑎1 𝛽1 = 𝑏 − 𝑎2
b) The system eigenvalues can be computed from:
|𝜆𝐈 − 𝐀| = |
𝜆 −1
𝑏 𝜆 + 𝑎
| = 𝜆(𝜆 + 𝑎) + 𝑏 = 𝜆2
+ 𝑎𝜆 + 𝑏 = 0
∴ 𝜆 =
−𝑎 ± √𝑎2 − 4𝑏
2
c) The transfer function can be derived from the state model as follows:
𝐺(𝑠) = 𝐂(𝐬𝐈 − 𝐀)−𝟏
𝐁 + 𝐃
Now 𝐬𝐈 − 𝐀 = [
𝑠 −1
𝑏 𝑠 + 𝑎
]
(𝐬𝐈 − 𝐀)−1
=
1
𝑠2+𝑎𝑠+𝑏
[
𝑠 + 𝑎 1
−𝑏 𝑠
]
∴ 𝐺(𝑠) = [1 0]
1
𝑠2 + 𝑎𝑠 + 𝑏
[
𝑠 + 𝑎 1
−𝑏 𝑠
] [
𝑎
𝑏 − 𝑎2] =
𝑎𝑠 + 𝑏
𝑠2 + 𝑎𝑠 + 𝑏
d) The system poles are the same as the eigenvalues.
e) If a = 2 & b = 4, then:
𝐀 = [
0 1
−4 −2
] 𝐁 = [
𝑎
𝑏 − 𝑎2] = [
2
4 − 4
] = [
2
0
] 𝐂 = [1 0] 𝐷 = 0
The transfer function becomes:
𝐺(𝑠) =
2𝑠 + 4
𝑠2 + 2𝑠 + 4
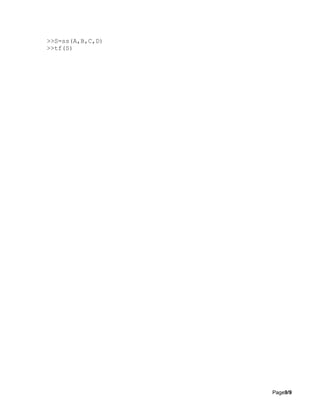
f) >>A=[0 1;-4 -2]
>>B=[2;0]
>>C=[1 0]
>>D=[]
>>S=ss(A,B,C,D)
>>tf(S)

7. Page7/9
Question 5 (15 points):
a) 𝐺(𝑠) =
3𝑠+2
𝑠2+7𝑠+12
=
𝑏 𝑜 𝑠2+𝑏1 𝑠+𝑏2
𝑠2+𝑎1 𝑠+𝑎2
∴ 𝑎1 = 7 𝑎2 = 12 𝑏1 = 2 𝑏2 = 2 𝑏 𝑜 = 0
𝐀 = [
0 1
−𝑎2 −𝑎1
] = [
0 1
−12 −7
] 𝐂 = [1 0] 𝐃 = 𝑏 𝑜 = 0 = 𝛽 𝑜
𝐁 = 𝛃 = 𝐛 − 𝐋𝛃′
∴ [
𝛽1
𝛽2
] = [
𝑏1
𝑏2
] − [
𝑎1 0
𝑎2 𝑎1
] [
𝛽 𝑜
𝛽1
] = [
3
2
] − [
7 0
12 7
] [
0
𝛽1
]
∴ 𝛽1 = 3 − 7 × 0 − 0 × 𝛽1 = 3
𝛽2 = 2 − 12 × 0 − 7𝛽1 = 2 − 7 × 3 = −19
∴ 𝐁 = [
3
−19
]
b) The controllable state model is given by:
𝐀 𝐜 = [
0 1
−𝑎2 −𝑎1
] = [
0 1
−12 −7
]
𝐁 𝐜 = [
0
1
]
𝐂 𝐜 = [ 𝑏2 − 𝑎2 𝑏 𝑜| 𝑏1 − 𝑎1 𝑏 𝑜] = [2 − 12 × 0|3 − 7 × 0] = [2 3]
𝐃 𝐜 = 𝑏 𝑜 = 0
c) The observable state model is given by:
𝐀 𝐎 = 𝐀 𝐜
𝐓
= [
0 −12
1 −7
]
𝐁 𝐎 = 𝐂 𝐜
𝐓
= [
2
3
] 𝐂 𝐎 = 𝐁 𝐜
𝐓
= [0 1] 𝐃 𝐎 = 𝑏 𝑜 = 0
d) 𝐺(𝑠) =
3𝑠+2
𝑠2+7𝑠+12
=
3𝑠+2
(𝑠+3)(𝑠+4)
=
10
𝑠+4
−
7
𝑠+3
=
𝑐1
𝑠+𝑝1
+
𝑐2
𝑠+𝑝2
𝐀 = [
− 𝑝1 0
0 − 𝑝2
] = [
−4 0
0 −3
] 𝐁 = [
1
1
] 𝐂 = [ 𝑐1 𝑐2] 𝐃 = 𝑏 𝑜 = 0
e) >>num=[3 2]

8. Page8/9
>>den=[1 7 12]
>>[A,B,C,D]=tf2ss(num,den)
Question 6 (15 points):
a) 𝐺(𝑠) =
𝑠2+4𝑠+2
(𝑠+1)(𝑠2+4𝑠+4)
=
𝑠2+4𝑠+2
(𝑠+2)2(𝑠+1)
=
𝑠2+4𝑠+2
(𝑠+𝑝1)2(𝑠+𝑝3)
=
2
(𝑠+2)2
+
2
𝑠+2
−
1
𝑠+1
=
𝑐1
( 𝑠+𝑝1)
2 +
𝑐2
𝑠+𝑝1
+
𝑐3
𝑠+𝑝3
∴ 𝐀 = [
− 𝑝1 1 0
0 − 𝑝1 0
0 0 − 𝑝3
] = [
−2 1 0
0 −2 0
0 0 −1
] 𝐁 = [
0
1
1
]
𝐂 = [ 𝑐1 𝑐2 𝑐3] = [2 2 −1] 𝐃 = 𝑏 𝑜 = 0
b) We first compute the eigenvalues as follows:
|𝜆𝐈 − 𝐀| = |
𝜆 −1
3 𝜆 + 4
| = 𝜆(𝜆 + 4) + 3 = 𝜆2
+ 4𝜆 + 3 = (𝜆 + 1)(𝜆 + 3) = 0 ===> 𝜆1 = −1
𝜆2 = −3
Then we construct the transformation matrix P such that x = Pz, where z is an auxiliary vector.
𝐏 = [
1 1
𝜆1 𝜆2
] = [
1 1
−1 −3
]
The state model becomes:
𝐳̇ = 𝐏−𝟏
𝐀𝐏𝐳 + 𝐏−𝟏
𝐁𝑢
𝑦 = 𝐂𝐏𝐳 + 𝐃𝑢
Now 𝐏−𝟏
𝐀𝐏 = [
− 𝜆1 0
0 − 𝜆2
] = [
−1 0
0 −3
] 𝐏−𝟏
𝐁 =
1
2
[
1
−1
] 𝐂𝐏 = [1 1] 𝐃 = 0
c) 𝐆(𝐬) = 𝐂(𝐬𝐈 − 𝐀)−1
𝐁 + 𝐃 = 𝐂(𝐬𝐈 − 𝐀)−1
𝐁
𝐬𝐈 − 𝐀 = [
𝑠 −1
2 𝑠 + 4
]
∴ 𝐆(𝐬) =
1
𝑠2 + 4𝑠 + 2
[
1 𝑠 + 4
𝑠 −2
]
d) >>A=[0 1;-2 -4]
>>B=[0 1;1 0]
>>C=[1 0;0 1]
>>D=[]

9. Page9/9
>>S=ss(A,B,C,D)
>>tf(S)