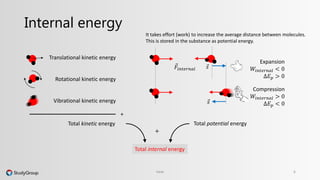
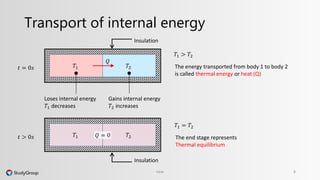
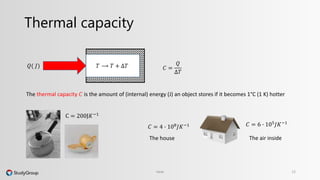
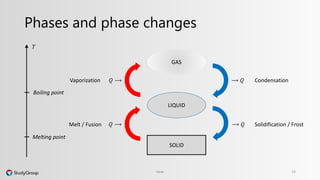
The document discusses various topics related to heat and temperature. It defines different temperature scales including Fahrenheit, Celsius, and Kelvin. It explains how to convert between temperature scales using formulas. It describes concepts such as thermal capacity, specific heat capacity, phases of matter, phase changes, and latent heats. An example problem demonstrates how to calculate the heat required to change the phase of water from liquid to vapor.

1. Heat
Photo: Wikimedia.org

2. Temperature scales
degree Fahrenheit
°F 1724
degree Celcius
°C 1742
Kelvin
K 1848
212
100
37.8
0
-17.78
32
Heat 2
-459.67
-273.15
0
100
373.15
310.93
255.37
0
273.15
푁푎퐶푙 ∙ 2퐻2푂
Absolute zero

3. Temperature conversion
푇 °퐶 = 푇 퐾 − 273.15 푇 퐾 = 푇 °퐶 + 273.15
Heat 3
푇 °퐶 =
5
9
∙ 푇 °퐹 − 32 푇 °퐹 =
9
5
∙ 푇 °퐶 + 32

4. Temperature conversion
푇 °퐶 = 푇 퐾 − 273.15 푇 퐾 = 푇 °퐶 + 273.15
Heat 4
푇 °퐶 =
5
9
∙ 푇 °퐹 − 32 푇 °퐹 =
9
5
∙ 푇 °퐶 + 32

5. Cold vs. Hot: Random motion
LOW  Kinetic energy  HIGH
SOLID
COLD HOT
LIQUID
Heat 5
GAS

6. Internal energy
It takes effort (work) to increase the average distance between molecules.
This is stored in the substance as potential energy.
Heat 6
Translational kinetic energy
Rotational kinetic energy
Vibrational kinetic energy
+
Total kinetic energy
퐹 푖푛푡푒푟푛푎푙 푠
Expansion
푊푖푛푡푒푟푛푎푙 < 0
Δ퐸푝 > 0
푠
Compression
푊푖푛푡푒푟푛푎푙 > 0
Δ퐸푝 < 0
Total potential energy
+
Total internal energy

7. Macroscopic vs. microscopic
푣 2 푣 7
푁 molecules
푣 10
푣 6
푣 9
푣 8
푣 3
푣 4
푣 1
푣 5
푣 11
Heat 7
푖
푣 푖 = 0
푖
푣 푖
2 = 푁 ∙ 푣푎푣푔
2 > 0
NO macroscopic motion
푁 ∙ 1
2
2 = 퐸푘푖푛 = measure for temperature
푚푣푎푣푔
Temperature is a macroscopic quantity
Temperature is a result of statistical mechanics

8. Transport of internal energy
Insulation
Heat 8
푄
푡 = 0푠 푇1 푇2
Loses internal energy
푇1 decreases
Gains internal energy
푇2 increases
푡 > 0푠 푇1 푄 = 0 푇2
푇1 > 푇2
The energy transported from body 1 to body 2
is called thermal energy or heat (Q)
푇1 = 푇2
The end stage represents
Thermal equilibrium
Insulation

9. Heat & Work - I
Explanation: Gravitational potential energy
is converted into internal energy
Heat 9
James Prescott Joule, 1847
Action: Release the crank
Reaction: The water temperature increases

10. Heat & Work - II
Heat is converted into work…but never completely
Heat 10

11. Thermal properties of matter
HEAT from combustion provides…
Specific latent heat
3: vaporization = destruction of molecular bonds
Specific heat capacity
2: increased internal energy of the water
Thermal capacity
1: increased internal energy of the pot
Heat 11

12. Thermal capacity
퐶 =
푄
Δ푇
Heat 12
푄( 퐽) 푇 ⟶푇 + Δ푇
The thermal capacity 퐶 is the amount of (internal) energy (J) an object stores if it becomes 1°C (1 K) hotter
C = 200J퐾−1
퐶 = 4 ∙ 108퐽퐾−1 퐶 = 6 ∙ 105퐽퐾−1
The house The air inside

13. Specific heat capacity
Heat 13
푄( 퐽) 푇 ⟶푇 + Δ푇
The specific heat capacity 푐 is the amount of (internal) energy (J) an material per kg stores if it becomes 1°C (1 K) hotter
퐶 = 푐 ∙ 푚 =
푄
Δ푇
⇒ 푐 =
푄
푚 ∙ Δ푇
If the body consists of one single substance/material:
퐶 ∝ 푚 or 퐶 = 푐 ∙ 푚
The constant 푐 is specific for this material and can be
found in data tables
푊푎푡푒푟 푐 = 4.18 ∙ 103퐽퐾−1푘푔−1
푉표푙푢푚푒 푉 = 휋푟2ℎ = 휋 ∙ 1푚 2 ∙ 0,6푚 = 1.9푚3
푀푎푠푠 푚 = 휌 ∙ 푉 = 998푘푔푚−3 ∙ 1.9푚3 = 1.9 ∙ 103푘푔
푇ℎ푒푟푚푎푙 푐푎푝푎푐푖푡푦 푝표표푙 퐶 = 푐 ∙ 푚 = 4.18 ∙ 103퐽퐾−1푘푔−1 ∙ 1.9 ∙ 103푘푔 = 8 ∙ 106퐽퐾−1

14. Phases and phase changes
GAS
Vaporization Condensation
LIQUID
SOLID
Heat 14
푄 ⟶
푄 ⟶
⟶ 푄
Melt / Fusion ⟶푄 Solidification / Frost
푇
Boiling point
Melting point

15. Specific latent heat
Heat required to melt/fuse 1 kg = ‘Latent heat of fusion’ 퐿푓 ,
which is needed to weaken the intermolecular bonds and increase potential energy
Heat required to vaporize 1 kg = ‘Latent heat of vaporization’ 퐿푣 ,
which is needed to break the already weakend bonds and set the molecules free
Material 푇푚푒푙푡(퐾) L푓 푘퐽푘푔−1 푇푏표푖푙 (퐾) L푣 푘퐽푘푔−1
Water 273.15 334 373.15 2260
Sulphur 386 39 718 1510
Nitrogen 63 26 77 199
Heat 15

16. Example
33.4 ∙ 106퐽
Heat 16
How much energy (heat) does it take to convert
100 kg water of 10°C to steam of 200°C?
Water
Specific heat capacity (liquid) 4.18 푘퐽푘푔−1퐾−1
Specific heat capacity (vapor) 1.5 푘퐽푘푔−1퐾−1
Latent heat of fusion 334 푘퐽푘푔−1
Latent heat of evaporation 2260 푘퐽푘푔−1
Heat water from 20°C to 100° : 푄 = 푐 ∙ 푚 ∙ Δ푇 = 4.18 ∙ 103 ∙ 100 ∙ 100 − 10 =
Vaporize the boiling water: 푄 = 퐿푣 ∙ 푚 = 334 ∙ 103 ∙ 100 =
Heat vapor from 100°C to 200° : 푄 = 푐 ∙ 푚 ∙ Δ푇 = 1.5 ∙ 103 ∙ 100 ∙ 200 − 100 =
37.62 ∙ 106퐽
15 ∙ 106퐽
+
86 ∙ 106퐽

17. Example
Heat taken up by cup & water equals heat released by the iron
Heat 17
A piece of iron 200푔 900℃ is inserted in a cup
C = 460 JK−1 filled with 500mL water 18℃ .
At which temperature will there be thermal equilibrium?
Material 푐(푘퐽푘푔−1퐾−1)
Water 4.18
Iron 0.45
푄↑ = 푄↓
퐶 ∙ 푇푒푞 − 18 + 푐푤푎푡푒푟 ∙ 푚푤푎푡푒푟 ∙ 푇푒푞 − 18 = 푐푖푟표푛 ∙ 푚푖푟표푛 ∙ 900 − 푇푒푞
460 ∙ 푇푒푞 − 18 + 4.18 ∙ 103 ∙ 0.998 ∙ 0.500 ∙ 푇푒푞 − 18 = 0.45 ∙ 103 ∙ 0.200 ∙ 900 − 푇푒푞
460 ∙ 푇푒푞 − 18 + 2086 ∙ 푇푒푞 − 18 = 90 ∙ 900 − 푇푒푞
460 ∙ 푇푒푞 − 8280 + 2086 ∙ 푇푒푞 − 37548 = 81000 − 90 ∙ 푇푒푞
460 ∙ 푇푒푞 + 2086 ∙ 푇푒푞 + 90 ∙ 푇푒푞 = 81000 + 8280 + 37548
2636 ∙ 푇푒푞 = 126828
푇푒푞 = 48℃

18. END
Disclaimer
This document is meant to be apprehended through professional teacher mediation (‘live in class’)
together with a physics text book, preferably on IB level.
Heat 18