Download to read offline
Uploaded byMaurice Verreck
Complex numbers
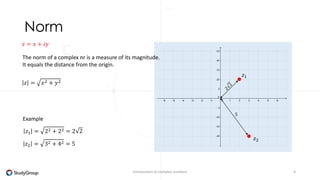
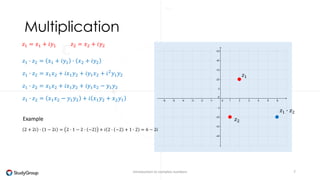
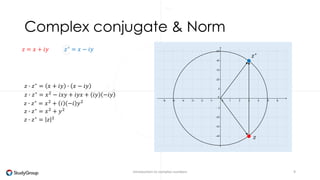
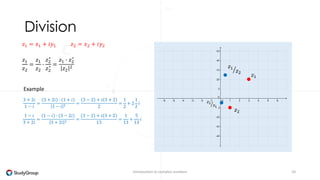
Complex numbers are numbers that consist of a real part and an imaginary part. The imaginary part is represented by the imaginary unit i, where i^2 = -1. The set of complex numbers C is the cartesian product of the real numbers R and imaginary numbers I. A complex number z can be written as z = x + iy, where x and y are real numbers representing the real and imaginary parts. Operations like addition, subtraction, multiplication and division can be performed with complex numbers by treating i as a variable and applying the standard rules of arithmetic.
More Related Content
Complex numbers
- 1. Introduction to complexnumbers wikimedia
- 2. Complex numbers Imaginea new number 푖 with the property 푖2 = −1 The set 푟 ∙ 푖 푟 ∈ ℝ is called the set of imaginary numbers 핀 ℝ ∩ 핀 = 0 ℝ ⊗ 핀 = ℂ ℂ is the set of complex numbers. It is the cartesian product of ℝ and 핀. This means that each element of ℂ consists 2 numbers: a real number coupled to an imaginary number. It can be written as a coordinate pair : z = 푥, 푦 with 푥, 푦 ∈ ℝ It is customary to write as a sum: 푧 = 푥 + 푖푦 with 푥, 푦 ∈ ℝ Introduction to complex numbers 2
- 3. Real & Imaginarypart Introduction to complex numbers 3 푧 = 푥 + 푖푦 is a complex number With … a real part 푅푒 푧 = 푥 an imaginary part Im 푧 = 푦 푧1 푧2 Example Real axis Imaginary axis Complex plane 푅푒 푧1 = 2 퐼푚 푧1 = 2 푅푒 푧2 = 3 퐼푚 푧2 = −4
- 4. Multiplication with areal number 푧 = 푥 + 푖푦 ∈ ℂ 푟 ∈ ℝ 푟 ∙ 푧 = 푟 ∙ 푥 + 푖푦 = 푟푥 + 푖푟푦 3푧 푧 Introduction to complex numbers 4
- 5. Norm The normof a complex nr is a measure of its magnitude. It equals the distance from the origin. Introduction to complex numbers 5 푧 = 푥 + 푖푦 푧1 푧2 푧 = 푥2 + 푦2 Example 푧1 = 22 + 22 = 2 2 푧2 = 32 + 42 = 5 5
- 6. Addition Compare head-to- tail method in physics Introduction to complex numbers 6 푧1 = 푥1 + 푖푦1 푧2 = 푥2 + 푖푦2 푧1 + 푧2 = 푥1 + 푖푦1 + 푥2 + 푖푦2 푧1 + 푧2 = 푥1 + 푥2 + 푖 푦1 + 푦2 푧1 푧2 푧1 + 푧2
- 7. Subtraction 푧1 −푧2 = 푥1 + 푖푦1 − 푥2 + 푖푦2 푧1 − 푧2 Introduction to complex numbers 7 푧1 = 푥1 + 푖푦1 푧2 = 푥2 + 푖푦2 푧1 푧2 푧1 − 푧2 = 푥1 − 푥2 + 푖 푦1 − 푦2 푧2 − 푧1 Compare difference vector in physics
- 8. Multiplication Introduction tocomplex numbers 8 푧1 = 푥1 + 푖푦1 푧2 = 푥2 + 푖푦2 푧1 ∙ 푧2 = 푥1 + 푖푦1 ∙ 푥2 + 푖푦2 푧1 ∙ 푧2 = 푥1푥2 + 푖푥1푦2 + 푖푦1푥2 + 푖2푦1푦2 푧1 푧2 푧1 ∙ 푧2 푧1 ∙ 푧2 = 푥1푥2 + 푖푥1푦2 + 푖푦1푥2 − 푦1푦2 푧1 ∙ 푧2 = 푥1푥2 − 푦1푦2 + 푖 푥1푦2 + 푥2푦1 Example 2 + 2푖 ∙ 1 − 2푖 = 2 ∙ 1 − 2 ∙ −2 + 푖 2 ∙ −2 + 1 ∙ 2 = 6 − 2푖
- 9. Complex conjugate ∗ The conjugate of a complex nr has a reversed imaginary part. ∗ Introduction to complex numbers 9 푧 = 푥 + 푖푦 푧1 푧2 Example 푧∗ = 푥 − 푖푦 푧1 푧2 −2 + 2푖 ∗ = −2 − 2푖 3 − 4푖 ∗ = 3 + 4푖 Note: 1: 푧∗ ∗ = 푧 2: if 푧∗ = 푧 then 푧 ∈ ℝ
- 10. Complex conjugate &Norm Introduction to complex numbers 10 푧 = 푥 + 푖푦 푧∗ 푧∗ = 푥 − 푖푦 푧 푧 ∙ 푧∗ = 푥 + 푖푦 ∙ 푥 − 푖푦 푧 ∙ 푧∗ = 푥2 − 푖푥푦 + 푖푦푥 + 푖푦 −푖푦 푧 ∙ 푧∗ = 푥2 + 푖 −푖 푦2 푧 ∙ 푧∗ = 푥2 + 푦2 푧 ∙ 푧∗ = 푧 2
- 11. Division 푧1 푧2 Introduction to complex numbers 11 푧1 = 푥1 + 푖푦1 푧2 = 푥2 + 푖푦2 푧1 푧2 푧1 푧2 = 푧1 푧2 ∙ 푧∗ 2 푧2 ∗ = ∗ 푧1 ∙ 푧2 푧2 2 Example 3 + 2푖 1 − 푖 = 3 + 2푖 ∙ 1 + 푖 1 − 푖 2 = 3 − 2 + 푖 3 + 2 2 = 1 2 + 2 1 2 푖 1 − 푖 3 + 2푖 = 1 − 푖 ∙ 3 − 2푖 3 + 2푖 2 = 3 − 2 + 푖 3 + 2 13 = 1 13 + 5 13 푖 푧2 푧1
- 12. END Disclaimer Thisdocument is meant to be apprehended through professional teacher mediation (‘live in class’) together with a mathematics text book, preferably on IB level. Introduction to complex numbers 12