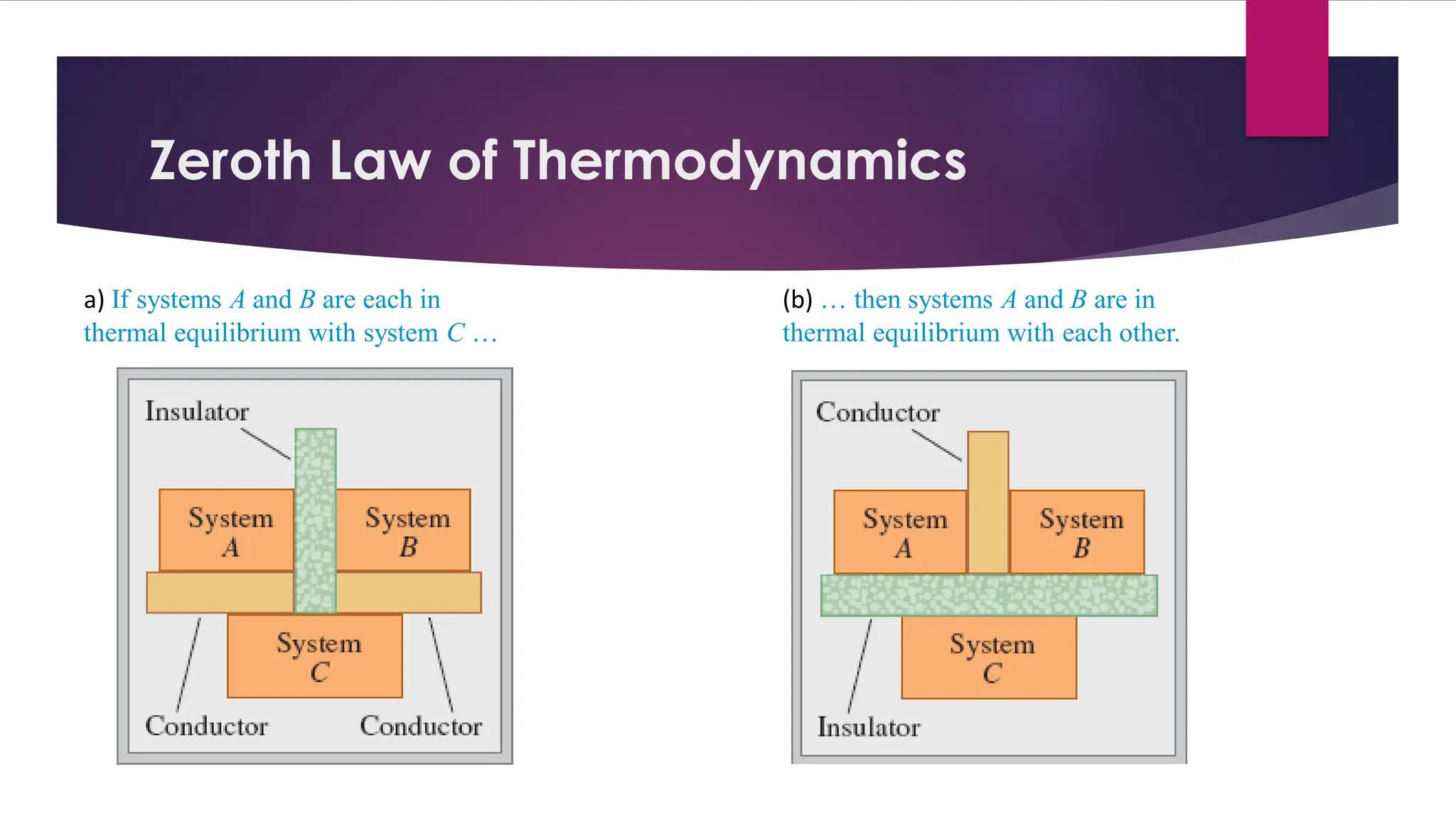
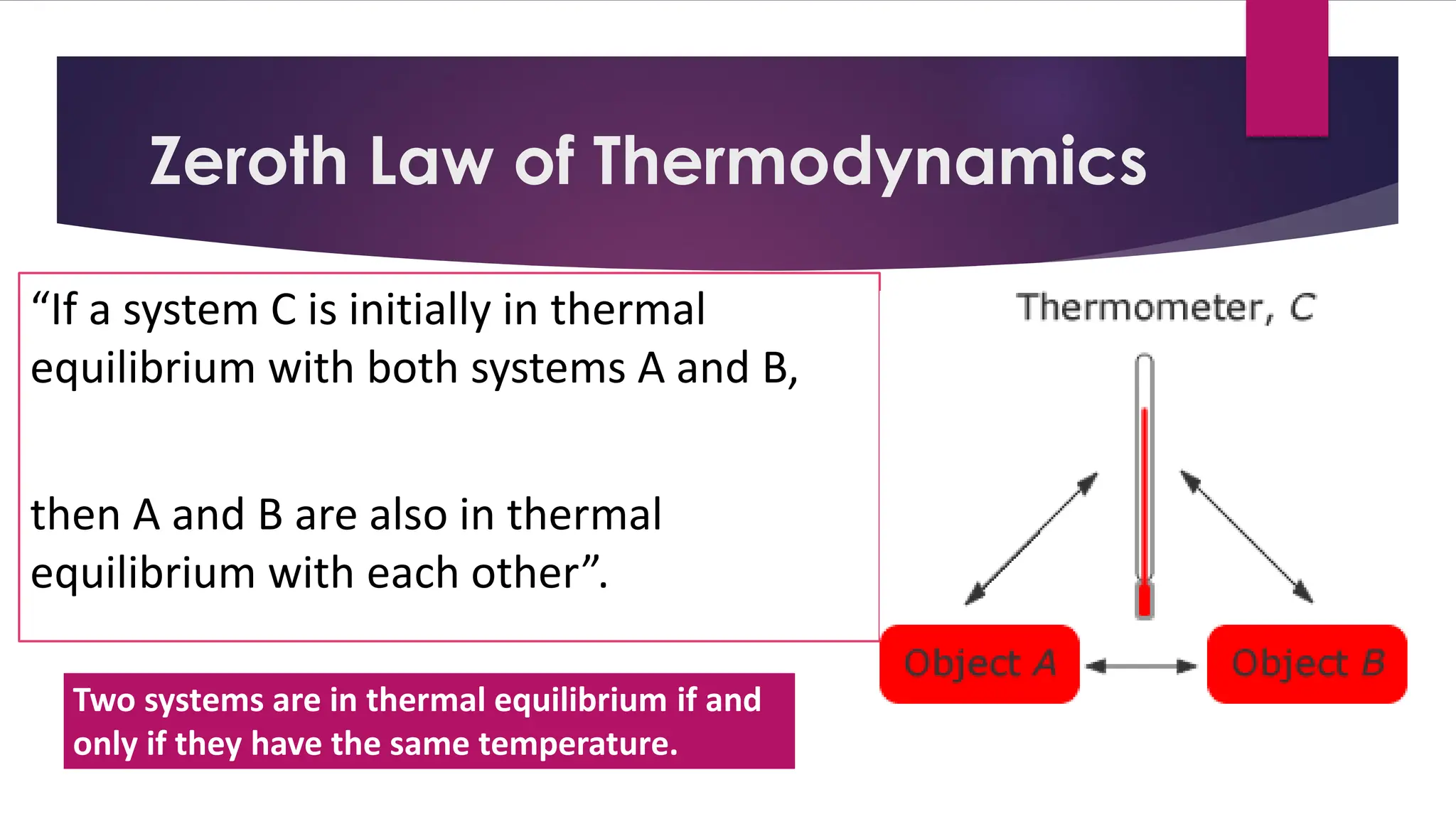
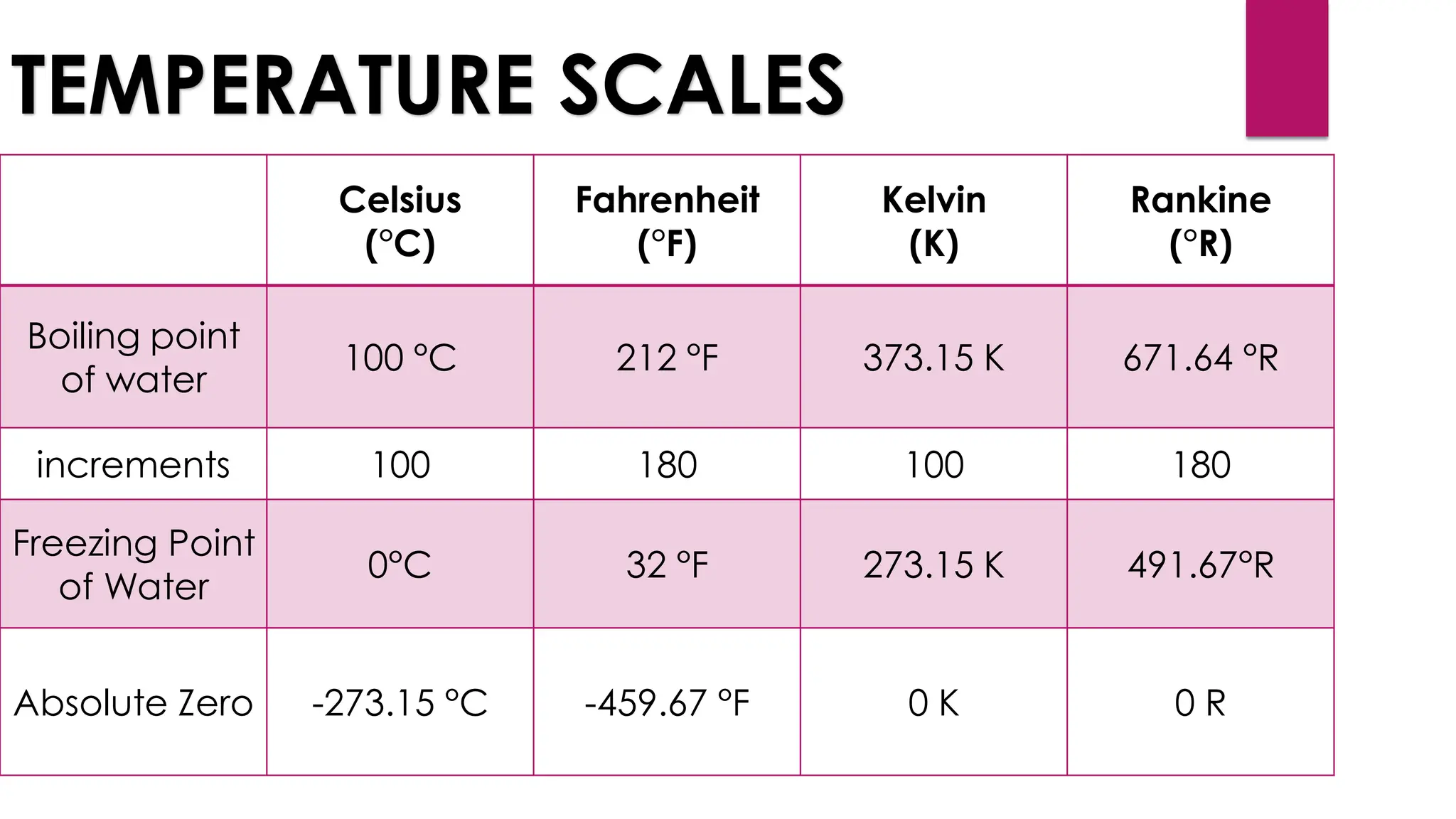
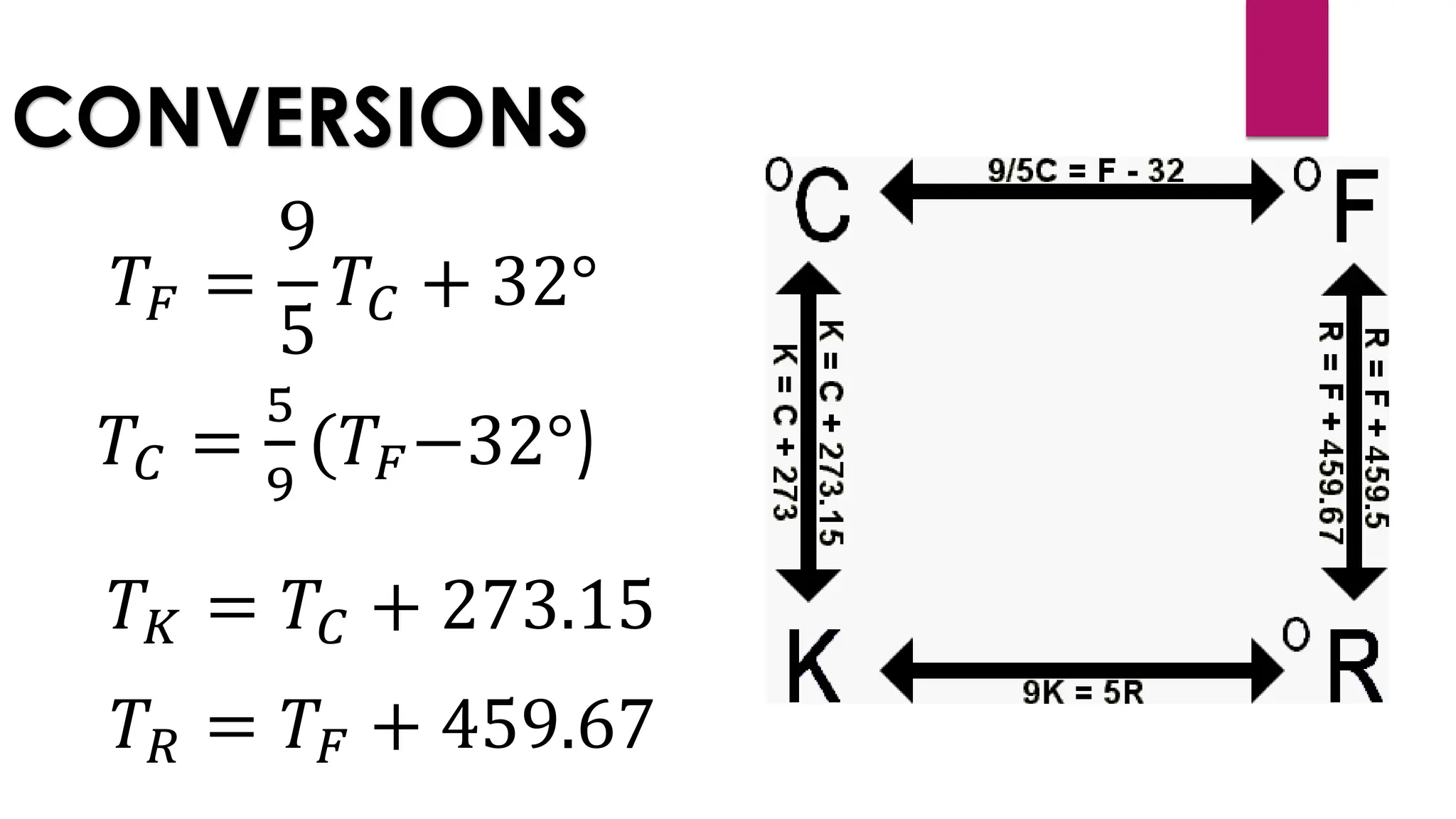
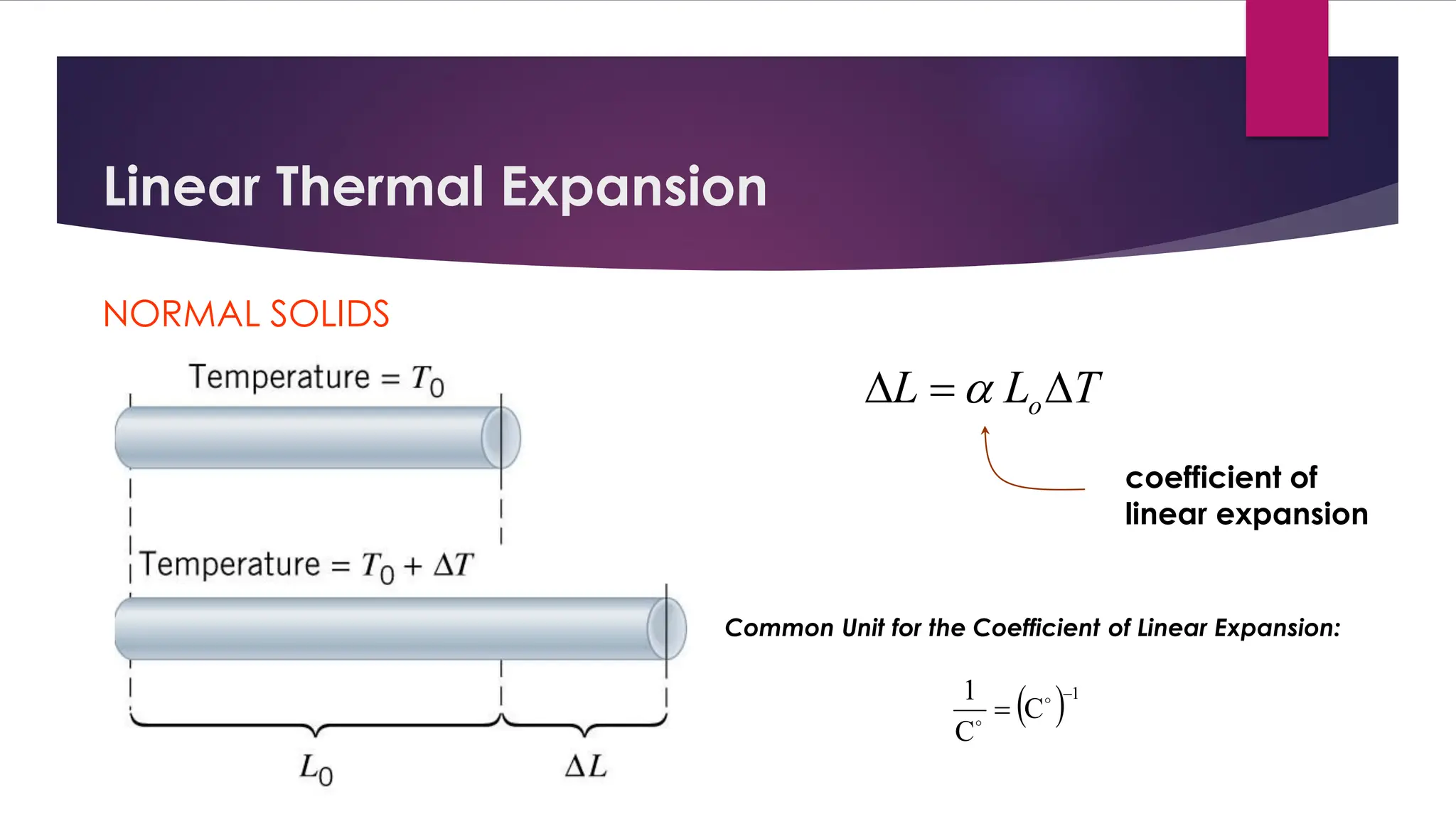
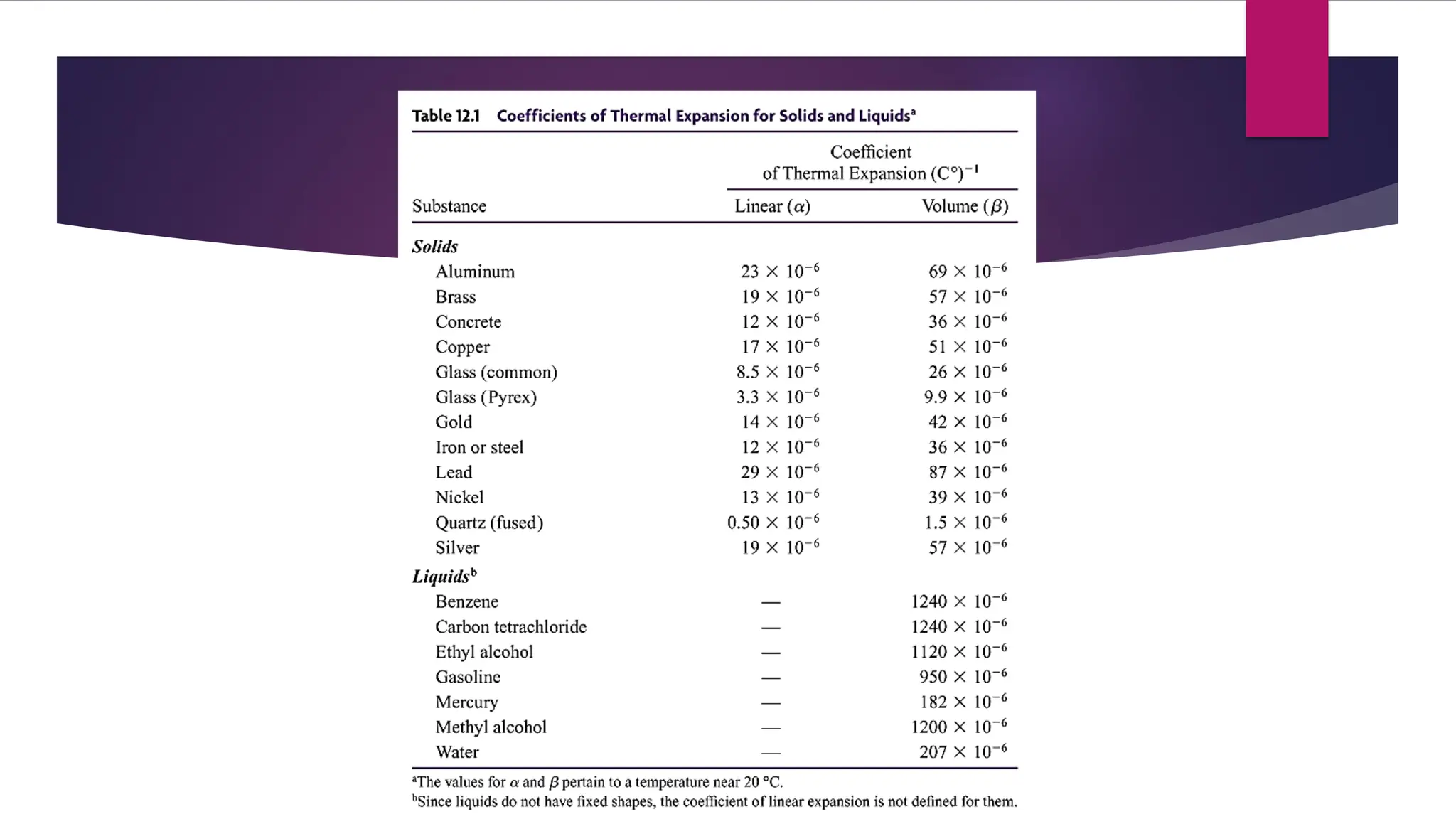
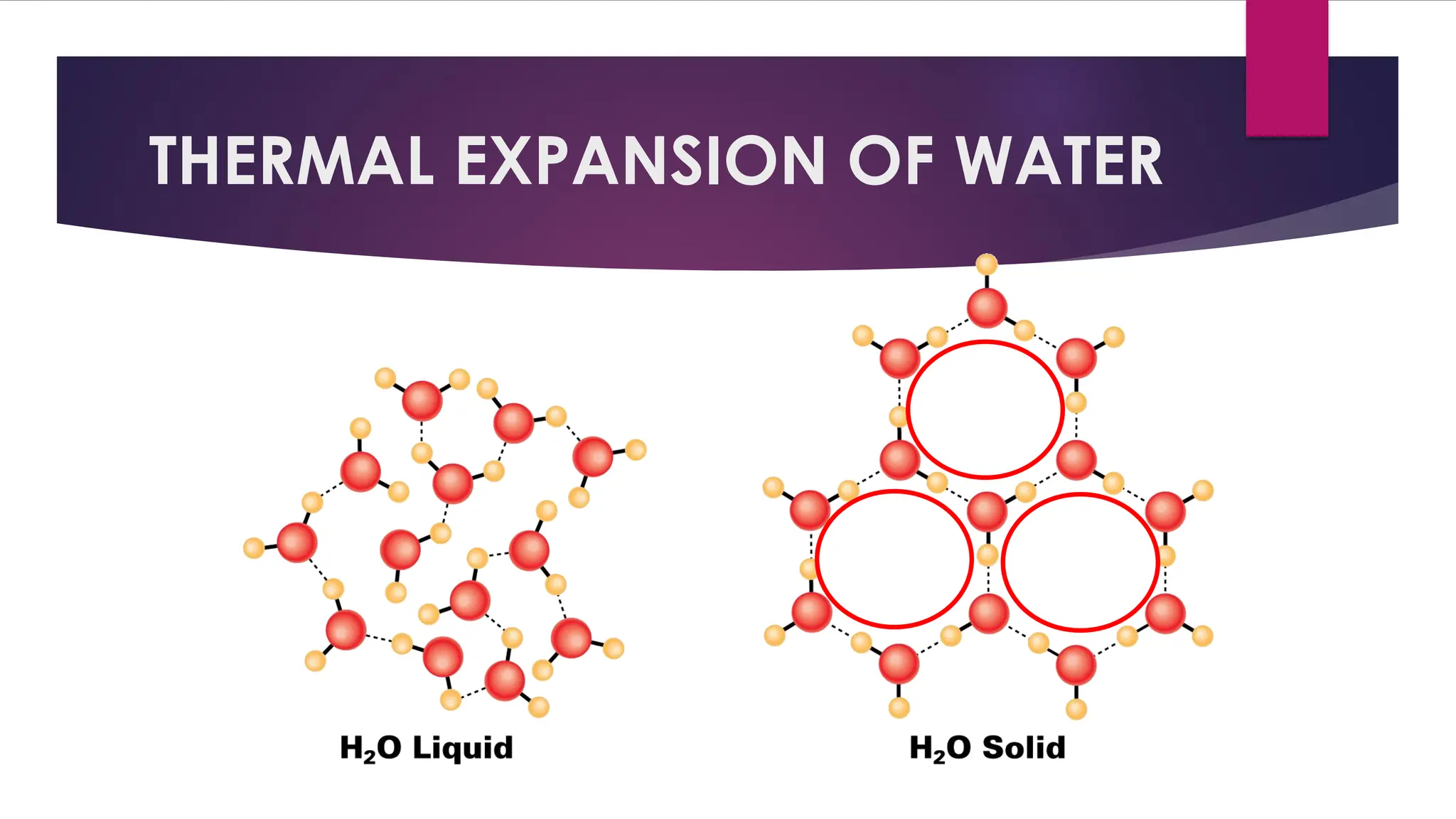
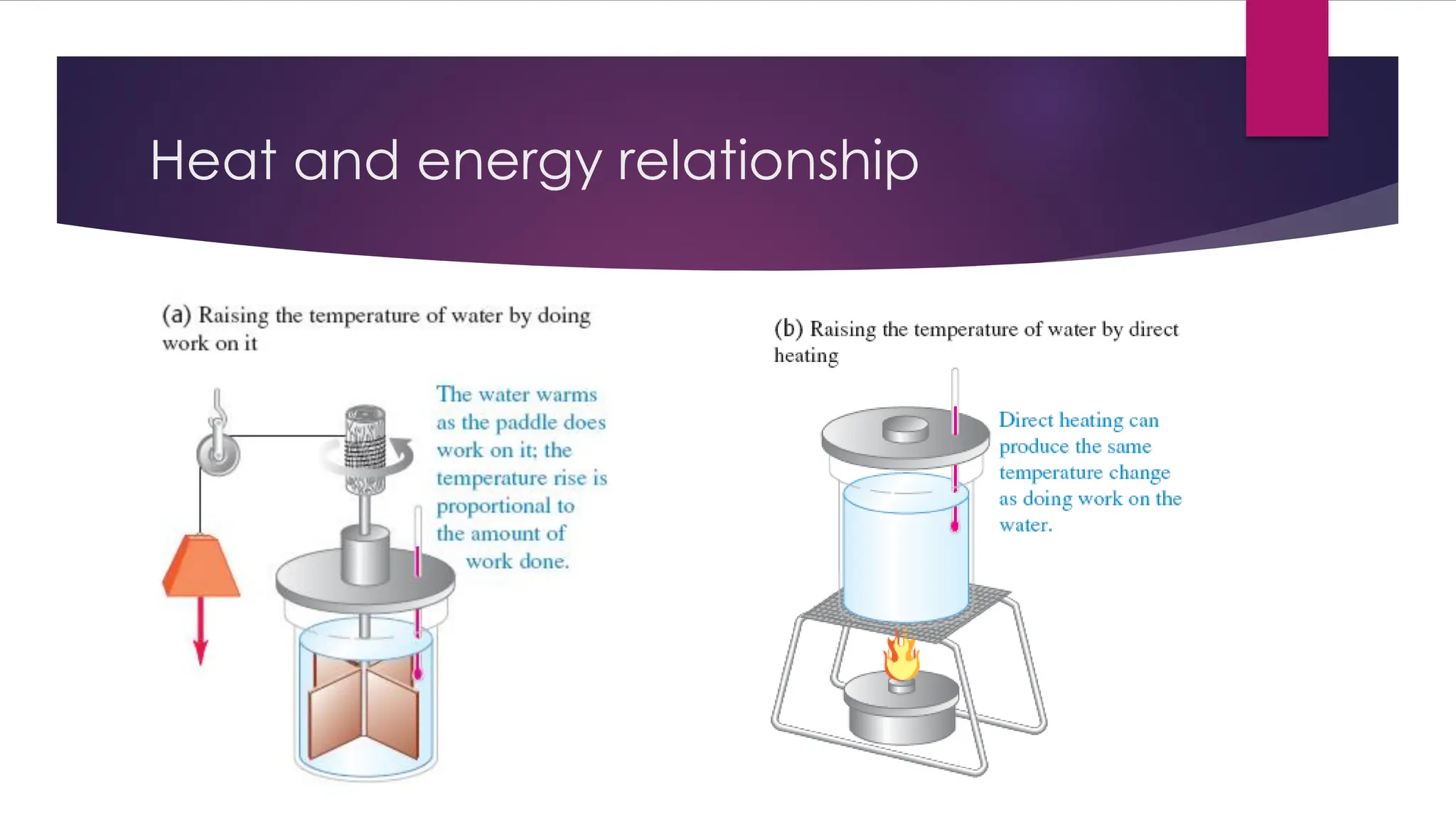
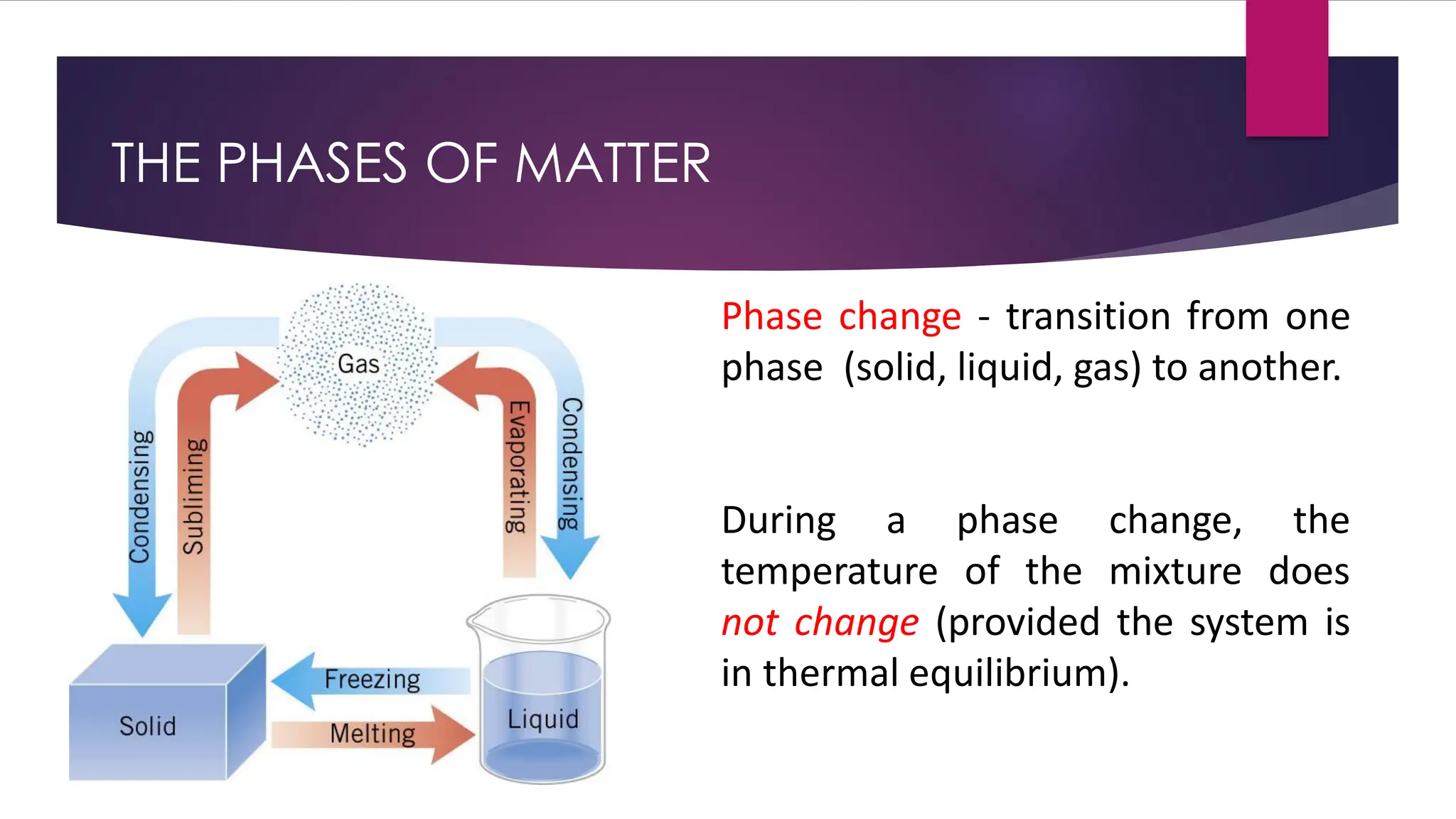
The document provides an overview of temperature and heat, including definitions, measurement methods, and the behavior of matter in different states related to thermal dynamics. It explains the zeroth law of thermodynamics, temperature scales, thermal expansion, heat transfer, and calorimetry. There are also sample problems to illustrate the calculations involved in determining specific heat and thermal energy changes during phase transitions.

1. TOPIC 8
TEMPERATURE AND HEAT

2. TEMPERATURE
 Quantitative measure of hotness or
coldness of a body
 Requires a device → thermometer

3. How does a thermometer work?
The thermometer is placed
in contact with the body
The thermometer becomes
hotter, the body cools off a
little
Thermal equilibrium

4. Zeroth Law of Thermodynamics
a) If systems A and B are each in
thermal equilibrium with system C …
(b) … then systems A and B are in
thermal equilibrium with each other.

5. Zeroth Law of Thermodynamics
“If a system C is initially in thermal
equilibrium with both systems A and B,
then A and B are also in thermal
equilibrium with each other”.
Two systems are in thermal equilibrium if and
only if they have the same temperature.

6. Temperature
Depends on
Particle
Movement!
➢ All matter is made up of
atoms that are
moving…even solid
objects have atoms that
are vibrating.
➢ The motion from the
atoms gives the object
energy.

7. All of the particles that make up matter are
constantly in motion
 Solid= vibrating atoms
 Liquid= flowing atoms
 Gas= move freely
 Plasma= move incredibly
fast and freely
The Kinetic Theory of Matter
www.nasa.gov

8. Anders Celsius
Daniel Gabriel
Fahrenheit
William Thomson,
1ST Baron Kelvin
William John
Macquorn Rankine

9. TEMPERATURE SCALES
Celsius
(°C)
Fahrenheit
(°F)
Kelvin
(K)
Rankine
(°R)
Boiling point
of water
100 °C 212 °F 373.15 K 671.64 °R
increments 100 180 100 180
Freezing Point
of Water
0°C 32 °F 273.15 K 491.67°R
Absolute Zero -273.15 °C -459.67 °F 0 K 0 R

10. CONVERSIONS
𝑇𝐹 =
9
5
𝑇𝐶 + 32°
𝑇𝐾 = 𝑇𝐶 + 273.15
𝑇𝑅 = 𝑇𝐹 + 459.67
𝑇𝐶 =
5
9
(𝑇𝐹−32°)

11. Note:
℃ ≠ C°
℃ - Temperature
reading
C° - Change in
temperature

12. THERMAL EXPANSION
 Change in physical dimensions
when subjected to change in
temperature
 Most materials expand when
heated

13.  The thermometer can measure
temperature because the
substance of the liquid inside
always expands (increases) or
contracts (decreases) by a
certain amount due to a change
in temperature.

15. Linear Thermal Expansion
NORMAL SOLIDS
T
L
L o
=
 
Common Unit for the Coefficient of Linear Expansion:
( )1
C
C
1 −
= 

coefficient of
linear expansion

17. THiNK!
If a metal sheet
with a hole in the
middle is
subjected to heat,
what will happen
to the hole?

18. THiNK!

19. VOLUME THERMAL EXPANSION
T
V
V o
=
 
coefficient of volume expansion
Common Unit for the Coefficient of Volume Expansion: ( )1
C
C
1 −
= 

The volume of an object changes when its temperature changes:

20. THERMAL EXPANSION
 Linear
∆𝐿 = 𝛼𝐿0∆𝑇
 Area
∆𝐴 = 2𝛼𝐴0∆𝑇
 Volume
∆𝑉 = 3𝛼𝑉0∆𝑇 = 𝛽𝑉0∆𝑇

21. THERMAL EXPANSION OF WATER

22. What effect
does heat
have on
density?
➢ When a substance is
heated, it expands,
volume increases.
➢ Therefore it becomes
less dense

23. A metal rod is 40.125 cm long at 20.0⁰C and
40.148 cm long at 45.0⁰C. Calculate the average
coefficient of linear expansion of the rod for this
temperature change.
Sample Problem 1
∆L = α𝐿0∆𝑇 α =
∆𝐿
𝐿0∆𝑇
=
40.148 𝑐𝑚 − 40. 125 𝑐𝑚
40.125 𝑐𝑚(45℃ − 20℃)
α = 2.29 𝑥 10−5/𝐶°

24. Sample Problem 2
 A wire is 1.50 m long at 20 °C is
found to increase its length by 1.9
cm when warmed to 420 °C.
 Compute the average coefficient
of linear expansion for its
temperature change.

25. Sample Problem 2
 Compute the average coefficient of
linear expansion for its temperature
change.
𝛼 =
∆𝐿
𝐿0∆𝑇
=
1.9 × 10−2
𝑚
1.50 𝑚 420℃ − 20℃
= 3.167 × 10−5
/C°

26. HEAT
DEFINITION OF HEAT
Heat is defined as the transfer of energy
across the boundary of a system due to
a temperature difference between the
system and its surroundings.
Heat flow/ heat transfer – energy
transfer that takes place solely because
of a temperature difference

27. ENERGY TRANSFER
HOT COLD

28. Heat and energy relationship

29. Heat is measured by the units of calorie
and joule (J).
calorie: The amount of energy needed
to raise the temperature of 1 gram of
water by 1Co (from 14.5oC to 15.5oC)
1 calorie= 4.186 J
Measuring Heat: units
British thermal unit (Btu): the
amount of energy required
to raise the temperature of
1lb of water by 1Fo (from
63oF to 64oF).
1 Btu = 0.252 kcal = 1055 J

30.  The heat capacity C of a particular sample of substance is
defined as the amount of energy needed to raise the
temperature of that by 1°C.
Heat capacity
T
C
Q 
=
T
Q
C

=

31. The specific heat capacity c of a substance is the heat
capacity per unit mass.
**a measure of how thermally insensitive a substance is to the addition of
energy
**the greater the material’s specific heat, the more energy must be added to
a given mass of the material to cause a particular temperature change..
Specific heat capacity
T
m
Q
c

=

32. Heat and Temperature Change: Specific
Heat Capacity
HEAT SUPPLIED OR REMOVED IN CHANGING THE
TEMPERATURE
OF A SUBSTANCE
The heat that must be supplied or removed to
change the temperature of a substance is
T
mc
Q 
=
SOLIDS AND LIQUIDS

33. Heat and Temperature Change: Specific
Heat Capacity
The value of the specific heat of a gas
depends on whether the pressure or volume
is held constant.
This distinction is not important for solids.
GASES

34. Sample Problem 3
An aluminum tea kettle with mass 1.50 kg and containing 1.80 kg of
water is placed on a stove. If no heat is lost to the surroundings, how
much heat must be added to raise the temperature from 20.0°C to
85.0°C?
𝑚𝐴𝑙 = 1.50 𝑘𝑔 𝑚𝑤 = 1.80 𝑘𝑔
𝑐𝐴𝑙 = 910
𝐽
𝑘𝑔𝐶° 𝑐𝑤 = 4190
𝐽
𝑘𝑔𝐶°
𝑇0 = 20 ℃ 𝑇 = 85 ℃
𝑄 = 𝑚𝐴𝑙 𝑐𝐴𝑙∆𝑇
𝑄 = (1.50 𝑘𝑔)(910
𝐽
𝑘𝑔𝐶°
)(85 ℃ − 20 ℃) = 8.873 𝑥 104
𝐽
Aluminum kettle
𝑄 = 𝑚𝑤 𝑐𝑤∆𝑇
𝑄 = (1.80 𝑘𝑔)(4190
𝐽
𝑘𝑔𝐶°
)(85 ℃ − 20 ℃) = 4.902 𝑥 105
𝐽
Water
𝑄𝑇 = 𝑄𝐴𝑙 + 𝑄𝑤 = 𝟓. 𝟕𝟗 𝒙 𝟏𝟎𝟓
𝑱
Total heat

35. Sample Problem 4
If 200 cm3of tea at 95⁰C is poured into a 150-g glass cup initially at 25⁰C, what
will be the common final temperature T of the tea and cup when equilibrium is
reached, assuming no heat flows to the surroundings?
𝑉𝑡𝑒𝑎 = 200 𝑐𝑚3
𝑇0𝑡𝑒𝑎 = 95℃
𝑐𝑤 = 4190
𝐽
𝑘𝑔𝐶°
𝑚𝑡𝑒𝑎 = 0.2 𝑘𝑔
𝑇0𝑐 = 25 ℃
𝑐𝑔 = 840
𝐽
𝑘𝑔𝐶°
𝑚𝑐 = 0.15 𝑘𝑔
𝜌 =
𝑚
𝑉
→ 𝑚𝑡𝑒𝑎 = 𝜌𝑉
= (1000
𝑘𝑔
𝑚3)(2 𝑥 10−4
𝑚3
)
෍ 𝑄 = 0
𝑄𝑡𝑒𝑎 + 𝑄𝑐𝑢𝑝 = 0
𝑚𝑡𝑒𝑎𝑐𝑤∆𝑇 + 𝑚𝑐𝑐𝑐∆𝑇 = 0
0.2 𝑘𝑔 4190
𝐽
𝑘𝑔𝐶°
𝑇 − 95℃ + (0.15 𝑘𝑔)(840
𝐽
𝑘𝑔𝐶°
)( 𝑇 − 25℃ = 0
838 𝑇 − 79610 𝐽 + 126 𝑇 − 3150 𝐽 = 0
𝑻 = 𝟖𝟔℃

36. CALORIMETRY
is the science of measuring
changes in parameters
of chemical reactions,
physical changes, and phase
transitions
for the purpose of deriving
the heat associated with
those changes.

37. SYSTEM – is any object or set of objects that we wish to consider.
Calorimetry: system
Closed system
No mass enters or leaves but energy can be exchanged with the
environment.
Isolated – if no energy in any form passes across its boundaries
Open system
Mass may enter or leave as may energy

38. CALORIMETRY
Conservation of energy
If there is no heat loss to the surroundings,
the heat lost by the hotter object equals the
heat gained by the cooler ones.
heat lost = heat gained
Simple water calorimeter
෍ 𝑄 = 0

39. THE PHASES OF MATTER
Phase change - transition from one
phase (solid, liquid, gas) to another.
During a phase change, the
temperature of the mixture does
not change (provided the system is
in thermal equilibrium).

40. When we add heat to ice at 0⁰C at normal
atmospheric pressure, the temperature of
the ice does not increase. Instead, some of
it melts to form liquid water.
The effect of adding heat to this system is
not to raise its temperature but to change
its phase (solid-liquid)

41. Phase Changes
 Transition between states
of matter
 Requires transfer of energy
 (+) heat entering the system
 (–) heat leaving the system 𝑄 = ±𝑚𝐿

42. Latent Heat of Fusion, Lf
 Required heat for
transition between
solid and liquid states
 (to fuse means “to combine
by melting”)
𝑄 = ±𝑚𝐿𝑓

43. Latent Heat of Vaporization, Lv
 Required heat for
transition between
liquid and gas states
 (the liquid “vaporizes”)
𝑄 = ±𝑚𝐿𝑣

44. WATER

45. How much energy is required to change a 40.0-g ice cube
from ice at -10.0⁰C to a steam at 110⁰C ?
Sample Problem 5
𝑄−10℃→0℃ = 𝑚𝑖𝑐𝑖∆𝑇
𝑄−10℃→0℃ = (0.04 𝑘𝑔)(2000 𝐽/𝑘𝑔 ∙ 𝐶°)(0℃ − −10℃ )
𝑄−10℃→0℃ = 800 𝐽
𝑄𝑖→𝑤 = 𝑚𝑖𝐿𝑓
𝑄𝑖→𝑤 = (0.04 𝑘𝑔)(334 𝑥 103
𝐽
𝑘𝑔
)
𝑄𝑖→𝑤 = 13,360 𝐽
𝑄0℃→100℃ = 𝑚𝑤𝑐𝑤∆𝑇
𝑄0℃→100℃ = (0.04 𝑘𝑔)(4190 𝐽/𝑘𝑔 ∙ 𝐶°)(100℃ − 0℃)
𝑄0℃→100℃ = 16,760 𝐽
𝑄𝑤→𝑠 = 𝑚𝑤𝐿𝑣
𝑄𝑤→𝑠 = (0.04 𝑘𝑔)(2256 𝑥 103
𝐽
𝑘𝑔
)
𝑄𝑤→𝑠 = 90,240 𝐽
𝑄100℃→110℃ = 𝑚𝑠𝑐𝑠∆𝑇
𝑄100℃→110℃ = (0.04 𝑘𝑔)(2010 𝐽/ 𝑘𝑔 ∙ 𝐶°)(110℃ − 100℃)
𝑄100℃→110℃ = 804 𝐽
𝑄𝑇 = 800 𝐽 + 13,360 𝐽 + 16,760 𝐽 + 90,240 𝐽 + 804 𝐽
= 𝟏𝟐𝟏, 𝟗𝟔𝟒 𝑱

46. Sample Problem 6
What mass of steam initially at 130⁰C is needed to warm 200 g of
water in a 100-g glass container from 20.0⁰C to 50.0⁰C?
𝑚𝑤 = 200 𝑔 = 0.2 𝑘𝑔
𝑚𝑔 = 100 𝑔 = 0.1 𝑘𝑔
𝑇𝑤 = 20.0℃
𝑇𝑔 = 20.0℃
𝑇0𝑠 = 130℃
𝑇 = 50.0℃
Steam:
𝑄130℃→100℃ = 𝑚𝑠𝑐𝑠∆𝑇
𝑄130℃→100℃ = 𝑚𝑠(2010 𝐽/ 𝑘𝑔 ∙ 𝐶°)(100℃ − 130℃)
𝑄130℃→100℃ = −𝑚𝑠(60,300
𝐽
𝑘𝑔
)
𝑄𝑠→𝑤 = −𝑚𝑠𝐿𝑣 = −𝑚𝑠 (2256 𝑥 103
𝐽/𝑘𝑔)
𝑄100℃→50℃ = 𝑚𝑠𝑐𝑤∆𝑇
𝑄100℃→50℃ = 𝑚𝑠(4190 𝐽/𝑘𝑔 ∙ 𝐶°)(50℃ − 100℃)
𝑄100℃→50℃ = −𝑚𝑠(209,500 𝐽/𝑘𝑔)
Sol’n:
i.
ii.
iii.

47. Water:
𝑄𝑤 = 𝑚𝑤𝑐𝑤∆𝑇
𝑄𝑤 = (0.200 𝑘𝑔)(4190 𝐽/ 𝑘𝑔 ∙ 𝐶°)(50℃ − 20℃)
𝑄𝑤 = 25,140 𝐽
𝑄𝑠 + 𝑄𝑔 + 𝑄𝑤 = 0
−𝑚𝑠(60,300
𝐽
𝑘𝑔
) − 𝑚𝑠 (2256 𝑥 103
𝐽/𝑘𝑔) −𝑚𝑠(209,500 𝐽/𝑘𝑔) + 2520 𝐽 + 25,140 𝐽 = 0
Glass:
𝑄𝑔 = 𝑚𝑔𝑐𝑔∆𝑇
𝑄𝑔 = (0.100 𝑘𝑔)(840 𝐽/ 𝑘𝑔 ∙ 𝐶°)(50℃ − 20℃)
𝑄𝑔 = 2520 𝐽
𝒎𝒔 = 𝟎. 𝟎𝟏𝟎𝟗𝟓 𝒌𝒈 𝒐𝒓 𝟏𝟎. 𝟗𝟓 𝒈