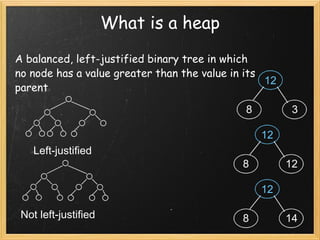
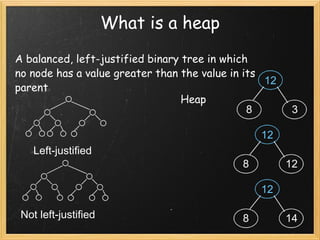
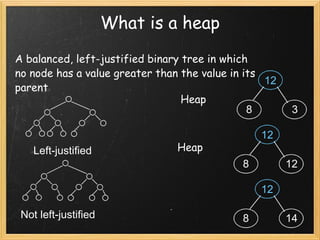
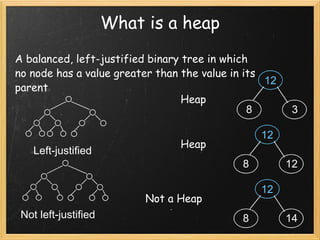
Heapsort is a sorting algorithm that uses a binary tree known as a heap. It has a worst-case runtime of O(n log n), making it useful for critical applications. A heap is a balanced, left-justified binary tree where each node's value is greater than or equal to its children. Heapsort inserts values into a heap and then removes the largest value to sort the data.

1. Heapsort

2. Heapsort Heapsort is a sorting algorithm that makes use of a binary tree. Heapsort is always O(n log n) there are other algorithms such as quicksort that perform better in good scenarios but in worst case perform at O(n 2) Heapsort is worst case O(n log n) so it is better for critical applications

3. What is a heap A balanced, left-justified binary tree in which no node has a value greater than the value in its parent Left-justified Not left-justified 12 8 3 12 8 12 12 8 14

4. What is a heap A balanced, left-justified binary tree in which no node has a value greater than the value in its parent Left-justified Not left-justified 12 8 3 12 8 12 12 8 14 Heap

5. What is a heap A balanced, left-justified binary tree in which no node has a value greater than the value in its parent Left-justified Not left-justified 12 8 3 12 8 12 12 8 14 Heap Heap

6. What is a heap A balanced, left-justified binary tree in which no node has a value greater than the value in its parent Left-justified Not left-justified 12 8 3 12 8 12 12 8 14 Heap Heap Not a Heap

7. Skipping Several pages of Algorithm Description for this class

8. Insert The following values into a heap 8, 10,5, 12

9. Insert The following values into a heap 8, 10,5, 12 8 Insert 8 at head of tree

10. Insert The following values into a heap 8, 10,5, 12 Insert Ten as child of 8. 8 10

11. Insert The following values into a heap 8, 10,5, 12 Insert Ten as child of 8. Then Shift Up 8 10 10 8

12. Insert The following values into a heap 8, 10,5, 12 Insert 5 as child of root Tree fits the properties of a heap no addional steps are needs 10 8 5

13. Insert The following values into a heap 8, 10,5, 12 Insert 12 a the left most child. 10 8 5 12

14. Insert The following values into a heap 8, 10,5, 12 Shift up until heap the tree becomes a heap. 10 8 5 12 10 12 5 8 12 10 5 8