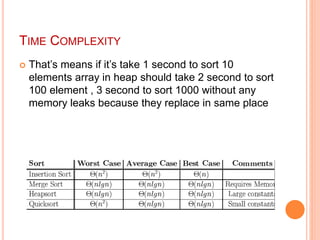
The document discusses heaps, a type of data structure used in heapsort, which organizes data into a binary tree format. It outlines two types of heaps—max-heaps and min-heaps—along with their properties, time complexity, and operational methods such as insertion and deletion. Additionally, it highlights the advantages of the heapsort algorithm and provides references for further reading.

1. HEAP
Data Structure And Algorithm
Mohamed Fawzy

2. AGENDA
 Introduction
 Heap Types
 Why Heap ?
 Time Complexity
 How to use it ?
 Applications on Heap
 Reference
 Questions

3. INTRODUCTION
 Heapsort : A sorting algorithm that works by first
organizing the data to be sorted into a special type
of binary tree called a heap.
 Heap: is an array object that we can view in special
form of complete binary tree e.g A[]

4. HEAP TYPES
 Max-Heap-root node has the largest value: A max
full complete binary tree where is root the largest
value for example A[Parent(i)] >= A[i]
 Min-Heap root node has the smallest value : A Min
full complete binary tree where is root the smallest
value for example A[Parent(i)] <= A[i]

5. HEAP TYPES (CONT)
 Parent(i)
return [i/2]
 Left(i)
Return 2i
 Right(i)
Return 2i+1

6. WHY HEAP ?
 Heap sort Algorithm has the best possible worst
case running time, and it doesn't need extra
storage. That makes it good for situations where
you have a very large array. Which used in Heap
Data structure .
 heapsort’s running time is O(n log n)

7. TIME COMPLEXITY
 That’s means if it’s take 1 second to sort 10
elements array in heap should take 2 second to sort
100 element , 3 second to sort 1000 without any
memory leaks because they replace in same place

8. HOW TO USE IT ?
 Let’s determine first how heap work
1. Remove the topmost item (the largest) and replace
it with the rightmost leaf. The topmost item is stored
in an array.
2. Re-establish the heap.
3. Repeat steps 1 and 2 until there are no more items
left in the heap.

9. HOW TO USE IT ? (CONT)
 The below image describe how it’s working to sort
max-heap data structure

10. HOW TO USE IT ? (CONT)
 Operations :
1- creation of an empty heap if not exist
2- insertion of a new element into heap if exist and
not full (overflow)
3- deletion of the largest(smallest) element from the
heap if exist and not empty (underflow)

11. HOW TO USE IT ? INSERTION INTO A MAX
HEAP
void insert_max_heap(int item, int *n)
{
int i;
if (HEAP_FULL(*n)) {
printf(“the heap is full.n”);
exit(1);
}
i = ++(*n);
while ((i!=1)&&(item.key>heap[i/2].key))
{
heap[i] = heap[i/2];
i /= 2;
}
heap[i]= item;
}

12. APPLICATIONS ON HEAP
 See an illustration first
 Array interpreted as a binary tree
1 2 3 4 5 6 7 8 9 10
26 5 77 1 61 11 59 15 48 19
26[1]
5[2] 77[3]
1[4] 61[5] 11[6] 59[7]
15[8] 48[9] 19[10]

13. APPLICATIONS ON HEAP
 Adjust it to a Max-Heap
77[1]
61[2] 59[3]
48[4] 19[5] 11[6] 26[7]
15[8] 1[9] 5[10]

14. REFERENCE
 Introduction to algorithms 3rd edition (Heapsort chapter)
 http://bigocheatsheet.com/
 http://cs.anu.edu.au/~Alistair.Rendell/Teaching/apac_comp3600/module2/bina
ry_heaps.xhtml
 http://www.eecs.wsu.edu/~cook/aa/lectures/l3.pdf
 http://www.iti.fh-flensburg.de/lang/algorithmen/sortieren/heap/heapen.htm
 http://www.slideshare.net/abdulwaqar/heap-sort-16149461
 Data structure and algorithms coursera (Princeton university )
 http://community.topcoder.com/tc?module=Static&d1=tutorials&d2=sorting

15. QUESTIONS
Any Questions ?