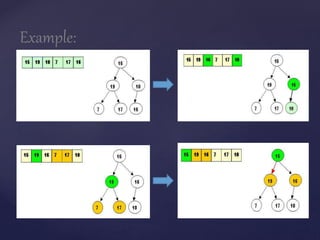
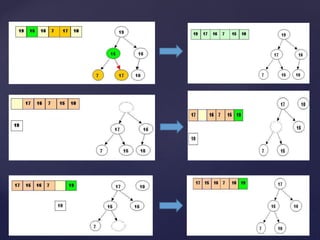
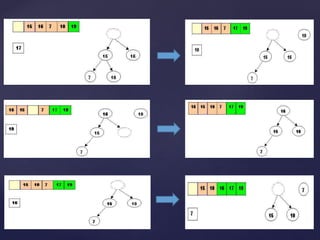
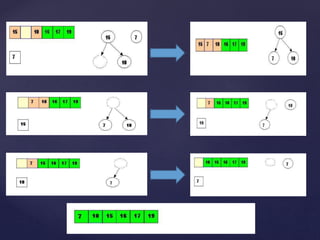
The document describes two sorting algorithms: quicksort and heapsort. Quicksort is a divide and conquer algorithm that works by selecting a pivot element and partitioning the array around it, recursively sorting the subarrays. The performance depends on how well balanced the partitions are. Heapsort uses a binary heap data structure to sort an array in-place. It works by building a max heap from the array and then removing elements from the heap one by one.

1. Presentation “Algorithm”
Group Members:
Abdul Basit Ali (Sp 13-BCS-045)
Ahsan Shahzad (Sp 13-BCS-037)

2. It is one of the fastest sorting techniques available.
Like binary search, this method uses a recursive, divide
and conquer strategy
The basic idea is to separate a list of items into two
parts, surrounding a distinguished item called the pivot.
At the end of the process, one part will contain items
smaller than the pivot and the other part will contain items
larger than the pivot.
The performance of the whole Quicksort algorithm
depends on how well the pivot is taken.

3. 1. Let us take the middle element as pivot.
2. Then we arrange the array such that all elements
greater then 8 is on right side and others on left
side.(This is the first subdivision producing two
sub list).
3. Now, each sub list is subdivided in exactly the
same manner. This process continues until all sub
lists are in order. The list is then sorted. This is
a recursive process.

4. We choose the value as pivot.(Preferably middle element).
As in binary search, the index of this value is found by
(first+last)/2
where first and last are the indices of the initial and
final items in the list.
We then identify a left_arrow and right_arrow on the
far left and far right, respectively.(left_arrow and
right_arrow initially represent the lowest and highest
indices of the vector items).
It looks like:

5. Starting on the right, the right_arrow is moved left until a
value less than or equal to the pivot is encountered.
In a similar manner, left_arrow is moved right until a value
greater than or equal to the pivot is encountered. This is
the situation just encountered. Now the contents of the two
vector items are swapped to produce

6. Example:

7. Since each element ultimately ends up in the correct position, the algorithm
correctly sorts. But how long does it take?.On this basis it is divided into
following three cases.
1. Best Case
2. Worst Case
3. Average Case
Best Case for QuickSort
The best case for divide-and-conquer algorithms comes when we split the input as evenly
as possible. Thus in the best case, each sub problem is of size n/2. The partition step on
each sub problem is linear in its size. the total efficiency(time taken) in the best case is
O(nlog2n).
Worst Case for Quicksort
Suppose instead our pivot element splits the array as unequally as possible. Thus instead
of n/2 elements in the smaller half, we get zero, meaning that the pivot element is the
biggest or smallest element in the array.
The Average Case for Quicksort
Suppose we pick the pivot element at random in an array of n keys Half the time, the pivot
element will be from the centre half of the sorted array. Whenever the pivot element is
from positions n/4 to 3n/4, the larger remaining sub-array contains at most 3n/4
elements.

8. Heap Sort

9. Heap Sort:
 Heaps are based on the notion of complete
tree.
 A Binary Tree has the Heap Property if,
* It is empty
* The key in the root is larger
than that in either and both
sub trees have the Heap property.

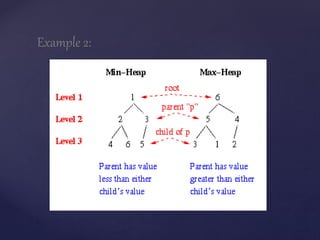
10. Types Of Heap:
 Min Heap :-
If the value at the node N, is less than or equal to
the value at each of the children of N, then Heap is
called a MIN-HEAP.
In General, a Heap represents a table of N
elements or records satisfying the following
property;
Nj  Ni for i  j  n & i = [j/2]

11.  Max Heap:-
If the value at the node N, is greater than or equal
to the value at each of the children of N, then Heap
is called a MAX-HEAP.
In General, a Heap represents a table of N
elements or records satisfying the following
property;
Nj  Ni for i  j  n & i = [j/2]

12. Two main steps for heap Sort are:
 Creation of Heap
 Processing of Heap

13. Creation of the Heap:
To put the largest element on the top
In each step size of the Heap increase.
 Put the elements in heap as they occur in sequential order
i.e. parent then left child and than right child.
 Each time (of inserting a new node/child) compare it with
its Parent Node;
Is? Child Node (Left child or Right child) is less
than or equal or greater than or equal to that of parent
node….
If it is greater than its successor than interchange
them.

14. Processing of the Heap:
The last element of last level should be replaced by
Top element of the list.
In this process the largest element will be at last
place
List will be sorted out in increasing order from Root
to Leaf.
After replacing the Top element Creation of the
Heap takes place.
In each step size of Heap decreased.

15. Example:

19. Example 2:

20. TIME COMPLEXITY :
Time complexity of heap sort in
• Worst case O(n log n)
• Average case O(n log n)
• Best case O(n log n)