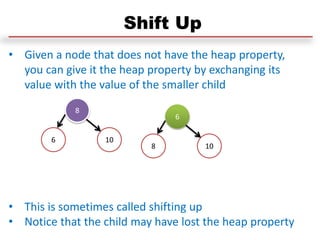
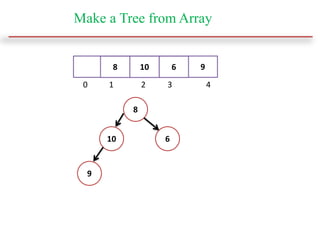
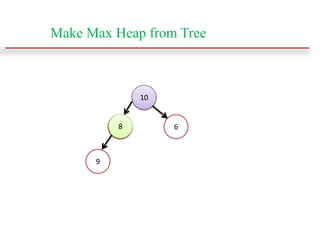
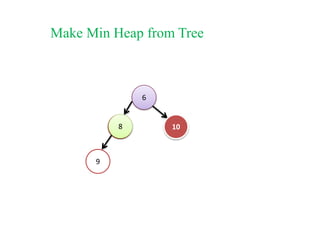
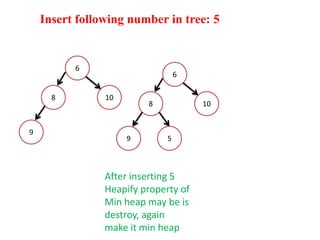
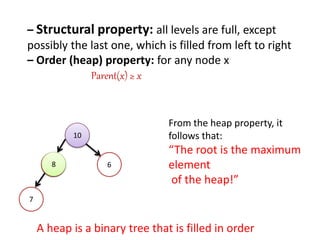
This document discusses heap sort and operations on heaps. It defines max-heaps and min-heaps, and how a heap can be represented as a binary tree and array. It explains that heap sort works by building a max-heap from an array, swapping the root with the last element and reducing the heap size, then sifting the new root down repeatedly until one element remains. Common heap operations like insertion, deletion, and heapify are also covered, along with time complexities of heap operations.

1. MUHAMMAD MUSADDIQ KHAN
ASSIGNMENT
SUBMITTED
BY
TO
SIR MUHAMMAD BILLAL

2. HEAP SORT
‫الرحیم‬ ‫الرحمن‬ ‫ہللا‬ ‫بسم‬

3. Def : A heap is a nearly complete binary tree
TYPES:
•Max-heaps (largest element at root), have the max-
heap
property:
– for all nodes i, excluding the root: A[PARENT(i)] ≥
A[i]
•Min-heaps (smallest element at root), have the
min-heap
property:
– for all nodes i, excluding the root: A[PARENT(i)] ≤
A[i]

4. – Structural property: all levels are full, except
possibly the last one, which is filled from left to right
– Order (heap) property: for any node x
Parent(x) ≥ x
A heap is a binary tree that is filled in order
From the heap property, it
follows that:
“The root is the maximum
element
of the heap!”
8
7
610
10
8

5. • Goal:
– Sort an array using heap representations
• Idea:
1– Build a max-heap from the array
2– Swap the root (the maximum element) with
the last element in the array
3– “Discard” this last node by decreasing the
heap size
4– Call MAX-HEAPIFY on the new root
5– Repeat this process until only one node
remains
Heapsort

6. Insertion.
Heapify.
Deletion.
Operations on Heaps

7. • New nodes are always inserted at the bottom
level
(left to right)
• Nodes are removed from the bottom level
(right to left)
Rule of Adding/Deleting Nodes

8. Array Representation of Heaps
• A heap can be stored as an
array A.
– Root of tree is A[1]
– Left child of A[i] = A[2i]
– Right child of A[i] = A[2i + 1]
– Parent of A[i] = A[ i/2 ]
The elements in the sub array
A[( n/2 +1) ….. n] are leaves

9. • Given a node that does not have the heap property,
you can give it the heap property by exchanging its
value with the value of the smaller child
• This is sometimes called shifting up
• Notice that the child may have lost the heap property
Shift Up
8
106
6
108
8

10. • Each time we add a node, we may destroy the
heap property of its parent node
• To fix this, we sift up
• We repeat the sifting up process, moving up in
the tree, until either
– We reach nodes whose values don’t need
to be swapped (because the parent is still
larger than both children), or
– We reach the root
Problem during Constructing a heap

11. 8
9
610
96108
0 1 2 3 4
Make a Tree from Array

12. 8
9
610
Make Max Heap from Tree
10
8

13. 8
9
610
Make Min Heap from Tree
6
8 10

14. 6
9
108
6
9
108
5
After inserting 5
Heapify property of
Min heap may be is
destroy, again
make it min heap
Insert following number in tree: 5

15. We can perform Major operations on
heaps:
 Heapify which runs in O(log n) time.
 Build-heap which returns in linear time.
 Heap sort, which runs in O(n log n) time.
Time Complexity

16. ANY
???