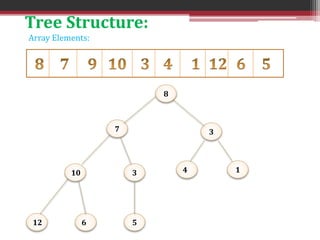
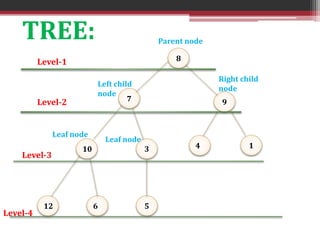
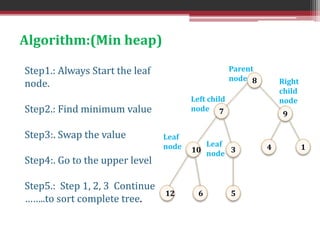
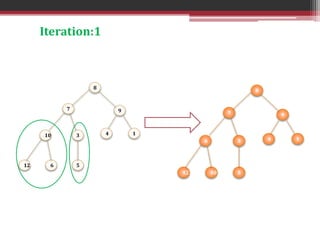
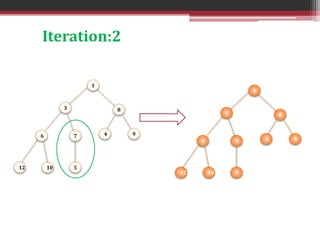
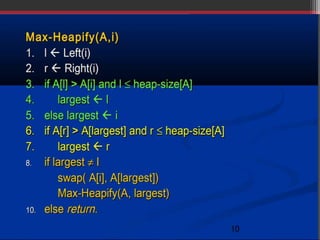
This document summarizes the heapify algorithm. The heapify algorithm rearranges a binary tree to maintain the heap property, where the root node is greater than or equal to its children (for a max heap) or less than or equal (for a min heap). It does this by comparing the root node to its children, swapping if needed, and then recursively heapifying the subtree. The complexity of the heapify algorithm is O(log n). Examples are provided of applying the heapify algorithm to transform an example tree into both a min heap and a max heap.

1. Heapify Algorithm
Sikandar Pandit
BCA(5th sem.)
15301216002
Syamaprasad Institute of Technology &
Mangaement
December 29, 2018

2. CONTENTS:
1.Introduction
2.Topic flow Structure
3.What is Heapify Algorithm
4.Tree Structure
5.Tree Explanation
6.Min heap Algorithm
7.Find min heap of Tree Applying Algorithm
8.Max heap Algorithm
9.Find max-heap of a tree with example
10.Complexity

3. Introduction:
Rearrange a heap to maintain the heap property, that is, the
key of the root node is more extreme (greater or less) than or
equal to the keys of its children. If the root node's key is not
more extreme, swap it with the most extreme child key, then
recursively heapify that child's subtree.

4. TOPIC FLOW STRUCTURE :
Data structure
Sorting Algorithm
Heap Sort
(Part of Binary Tree)
Heapify Algorithm
Find a heap of binary Tree
Find min heap Find max heap

5. Heapify
Algorithm
It is a method of finding the heap of a tree.

6. What is
Heapify
Algorithm?
Rearrange a heap to maintain the heap property, that is, the key of
the root node is more extreme (greater or less) than or equal to the
keys of its children. If the root node's key is not more extreme, swap it
with the most extreme child key, then recursively heapify that child's
subtree.

7. Tree Structure:
Array Elements:
8
37
410 3 1
12 6 5

8. TREE:
8
97
410 3 1
12 6 5
Parent node
Left child
node
Right child
node
Leaf node
Leaf node
Level-1
Level-2
Level-3
Level-4

9. Algorithm:(Min heap)
Step1.: Always Start the leaf
node.
Step2.: Find minimum value
Step3:. Swap the value
Step4:. Go to the upper level
Step5.: Step 1, 2, 3 Continue
……..to sort complete tree.
8
97
410 3 1
12 6 5
Parent
node
Left child
node
Right
child
node
Leaf
node Leaf
node

10. Iteration:1
8
97
410 3 1
12 6 5
8
97
46 3 1
12 10 5

11. 8
97
46 3 1
12 10 5
8
13
46 7 9
12 10 5

12. 1
83
46 7 9
12 10 5
8
13
46 7 9
12 10 5

13. 1
83
46 7 9
12 10 5
Iteration:2
1
83
46 5 9
12 10 7

14. 1
83
46 5 9
12 10 7
1
43
86 5 9
12 10 7

15. Complete
Binary sort
tree:
1
43
86 5 9
12 10 7

16. Algorithm: Max-Heapify

17. Step1.: Always Start the top
most node.
Step2.: Find maximum value
Step3:. Swap the value
Step4:. Come to the lower level
Step5.: Step 1, 2, 3 Continue
……..to sort complete tree.
Algorithm: (Max Heapify)

19. Complexity of
Heapify Algorithm.
0(log n)
When Heapify() are called .
During heap sort

20. Thanku
Presented By:-
Reg No:-
Topic:-