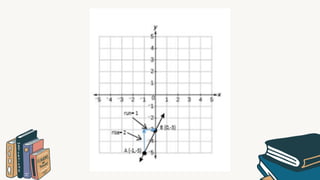
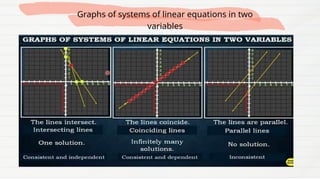
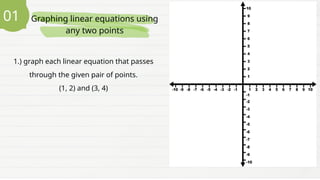
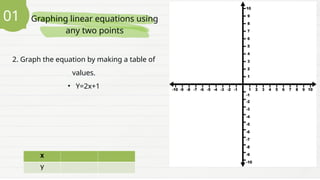
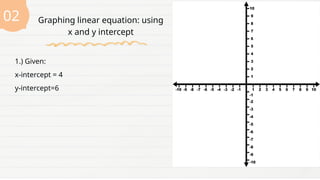
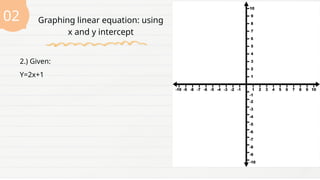
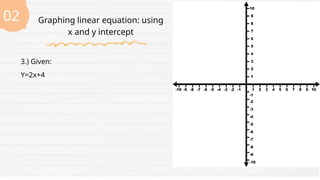
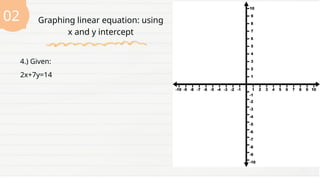
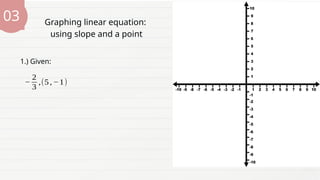
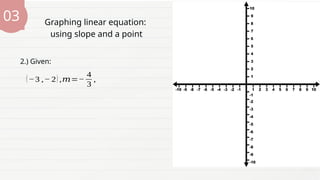
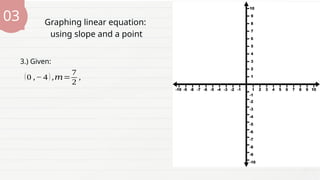
The document provides a lesson for Grade 8 students on graphing linear equations in two variables using three methods: two points, x and y intercepts, and slope with a point. It includes examples and exercises for each method, illustrating how to graph equations and interpret their intercepts. The lesson aims to equip students with the skills to apply these methods to real-life problems.

1. GOOD MORNING
GRADE 8!
Prepared by: Ms. Roxane G.
Navidad

2. After going through this module, you are
expected to:
• a. Identify the three methods of
graphing a linear equation.
• b. Graph a linear equation given
any two points, x and y intercepts,
the slope and a point and
• Select any method in graphing
linear equations in dealing with
real life problems.

3. Graphing Linear equations
in two variables
LESSON 4

4. Introduction
• Graph each linear equation that passes
through the given pair of points. Use graph
paper.
1.(2,2) and (4,5)
2.(0,1/2 ) and (2,3/2 )
3.(-1,2) and (5,0)
4.(-5, -3) and (-3, 5)

5. A linear equation in two variables can be written either in the form Ax+By=C or
y=mx+b where A, B and C are real numbers and A and B are not equal to zero.
Graphing linear equations can be done using any of the three methods.
1.USING ANY
TWO POINTS
OF THE LINE
2. USING X
AND Y
INTERCEPTS
3.USING A
SLOPE AND A
POINT
01 02 03

6. USING ANY TWO POINTS:
• One method of graphing a linear
equation is using any two points.
Remember that two points are enough to
draw the graph of a linear equation.
Line Postulate
• Two points determine a line.
01

7. Example 1:
Graph the linear equation y=2x-3.
Solution:
You may assign any two arbitrary values of x, say 0
and 1 and then solve for the corresponding value of
y.
By substitution,
y=2x-3
y=2(0)-3
y=0-3
y=-3
When x=1
y=2x-3
y=2(1)-3
y=2-3
y=-1
01

8. The solution shown
above implies that if x=0
then y=-3. Also, if x=1,
then y=-1. Thus, the
ordered pairs are (0, -3)
and (1,-1), respectively.
This means that the line
passes through these
points.
01

9. 02
USING X AND YINTERCEPT

10. The x intercept is the abscissa of
the point where the graph of the
line crosses the x-axis. This implies
that the point is on the x-axis then
the ordinate is 0, (x,0). Similarly,
since the y-intercept is the ordinate
of the point where the graph or the
line crosses the y-axis, this implies
that the point is on the y-axis, hence
the abscissa is 0, (0,y)
NOTE:
02

11. Example 2:
Solution:
To find the x-intercept of a line given its equation,
let y=0, then solve for x.
To find the y-intercept, let x=0, then solve for y
Letting y=0, the equation y= 2x-3 becomes
By substitution,
0=2x-3
-2x=-3
-2x/-2=-3/-2
x=3/2
Hence, the x-intercept is
3/2. In symbol, a=3/2,
then the point in the x-
axis is (3/2, 0)
02

12. 03
USING A SLOPE AND A
POINT

13. Graph the line whose slope is 2 and contains the
point (-1, -5)
1.Plot the given point (-1, -5).
2. Use the slope formula m= to identify the rise and the run. The
slope of a line is 2 which is equal to .
Note: If the slope is positive, the graphs move upward; if the
slope is negative, the graph moves downward.
3.Starting at the given point (-1, -5), count out the rise (2 units
up) and run
(1 unit to the right) to mark the second point. (Note that the
slope is positive)
4.Draw a line passing the points.
Example 3:
02

15. Graphs of systems of linear equations in two
variables

16. • In graphing system of linear equation, you may use any
method like the Intercept Method or Slope-Intercept
Method.
Graphing systems of linear equations in two
variables
2x+y=6
4x+y=8
Standard Form
Intercept Method
y=-2x+6
Y=-4x+8
Slope-Intercept Form
Slope-Intercept Method

17. 01
Graphing linear Equation:
Using any two points

18. Graphing linear equations using
any two points
01
1.) graph each linear equation that passes
through the given pair of points.
(1, 2) and (3, 4)

19. Graphing linear equations using
any two points
01
2. Graph the equation by making a table of
values.
• Y=2x+1
x
y

20. 02
Graphing linear Equation:
Using x and y intercept

21. 02
1.) Given:
x-intercept = 4
y-intercept=6
Graphing linear equation: using
x and y intercept

22. 02
2.) Given:
Y=2x+1
Graphing linear equation: using
x and y intercept

23. 02
3.) Given:
Y=2x+4
Graphing linear equation: using
x and y intercept

24. 02
4.) Given:
2x+7y=14
Graphing linear equation: using
x and y intercept

25. 03
Graphing linear Equation:
Using slope and a point

26. 03
1.) Given:
Graphing linear equation:
using slope and a point
−
2
3
,(5,−1)

27. 03
2.) Given:
Graphing linear equation:
using slope and a point
(−3 ,− 2) ,𝑚=−
4
3
,

28. 03
3.) Given:
Graphing linear equation:
using slope and a point
(0 ,− 4 ) ,𝑚=
7
2
,

29. Thanks For Listening!

30. Resource page