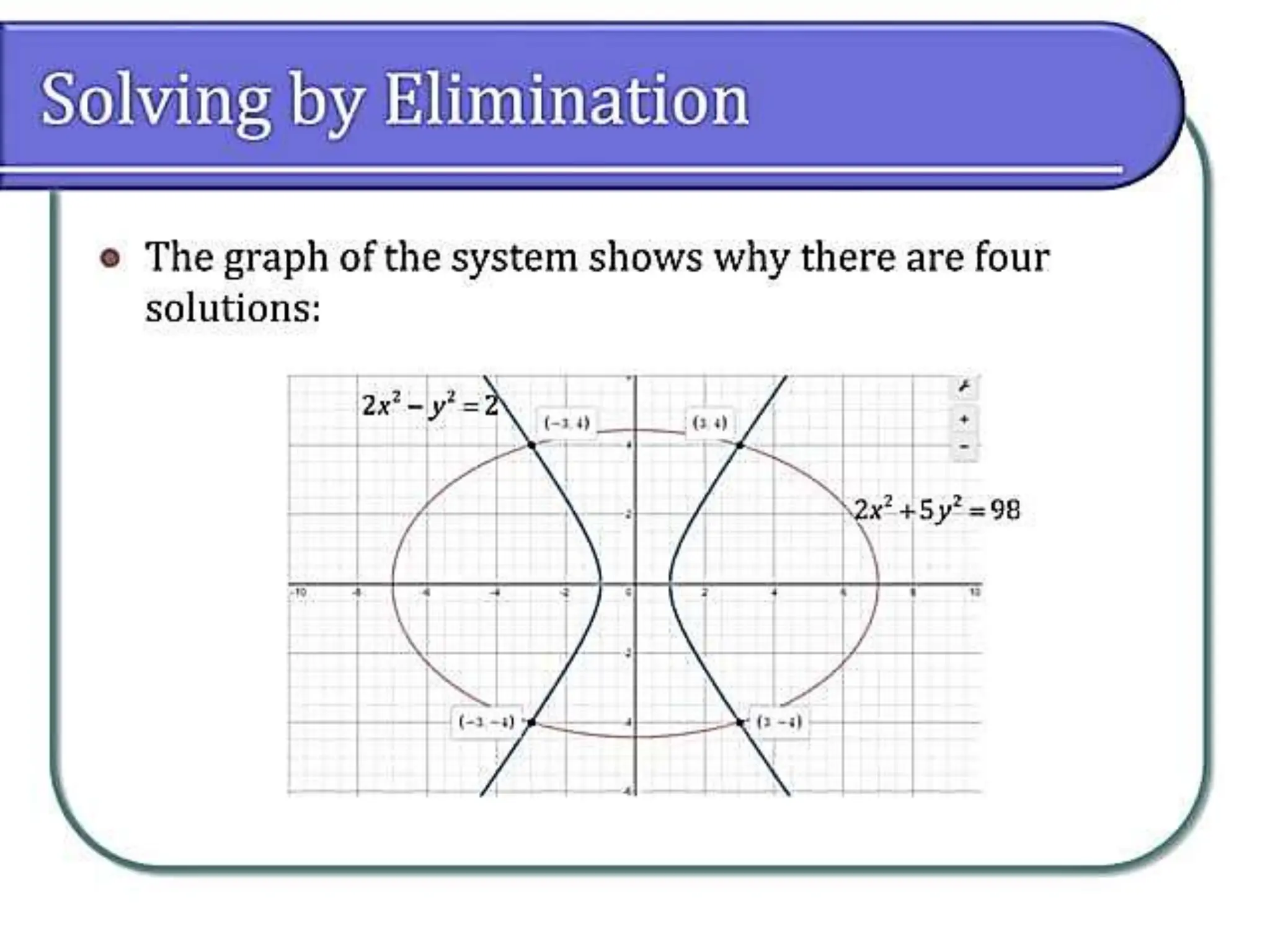
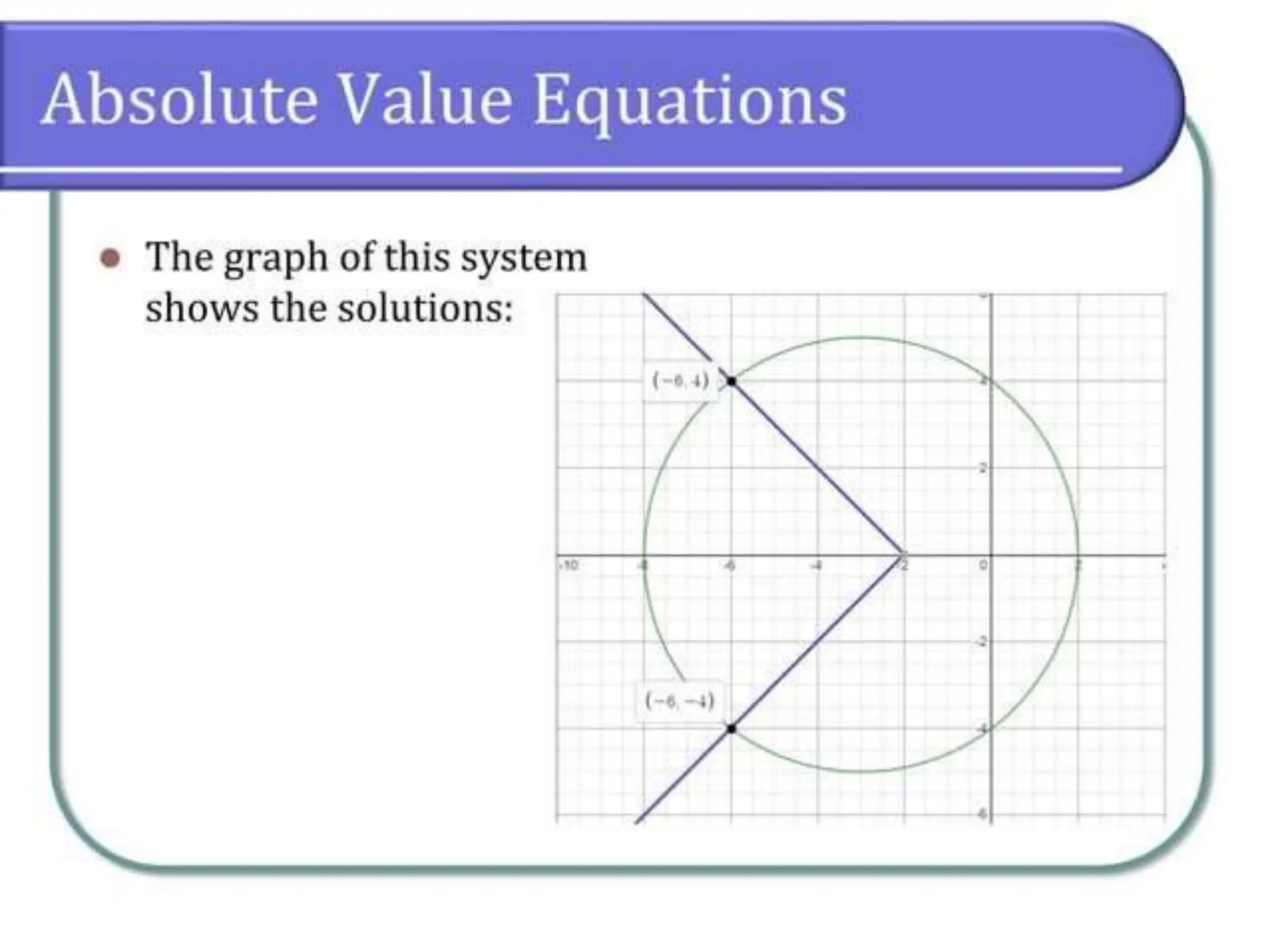
This document discusses methods for solving systems of nonlinear equations, including elimination, substitution, and graphing. It provides examples of using elimination and substitution to solve specific systems. Elimination involves rewriting equations and adding them to eliminate a variable, while substitution isolates a variable in one equation and substitutes it into the other equation. The examples find the point of intersection by solving the systems algebraically and graphing the equations on the same plane.

1. System of Nonlinear Equations
Eliminations
Substitution
Graphing

2. 1. illustrate systems of nonlinear equations;
2. determine the solutions of systems of nonlinear
equations using techniques such as substitution,
elimination, and graphing; and
3. solve situational problems involving systems of
nonlinear equations.

9. Use the elimination method to solve the system and sketch the
graphs in one Cartesian plane showing the point of intersection.
We eliminate first the variable x. Rewrite the first equation
wherein only the constant term is on the right-hand side of the
equation, then multiply it by −2, and then add the resulting
equation to the second equation.

10. Use the elimination method to solve the system and sketch the
graphs in one Cartesian plane showing the point of intersection.

15. Use the substitution method to solve the system and sketch
the graphs in one Cartesian plane showing the point of
intersection.

16. Isolate the variable y in the first equation, and then substitute
into the second equation.
4𝑥 + 𝑦 = 6
⟹ 𝑦 = 6 − 4𝑥
5𝑥 + 3𝑦 = 4
5𝑥 + 3 6 − 4𝑥 = 4
5𝑥 + 18 − 12𝑥 = 4
−7𝑥 + 18 = 4
𝑥 = 2
𝑦 = 6 − 4 2
𝑦 = −2