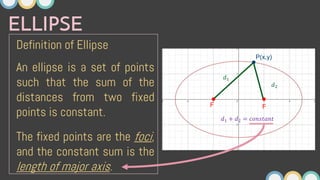
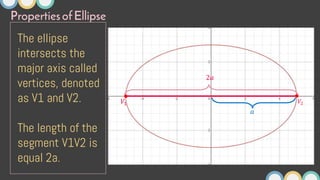
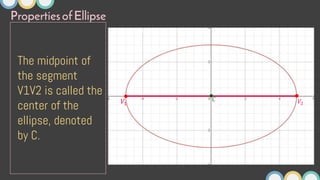
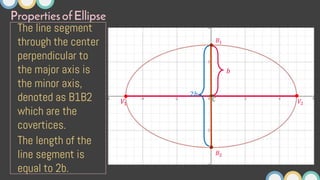
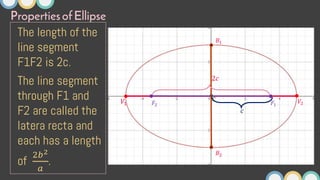
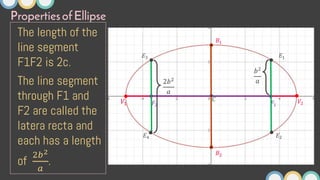
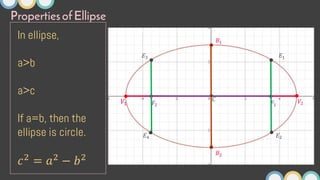
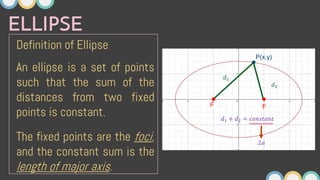
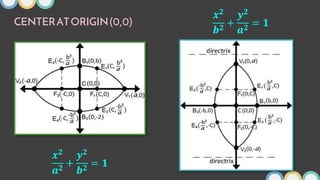
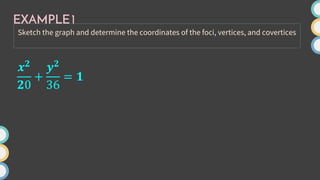
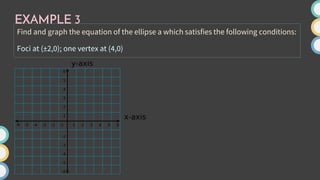
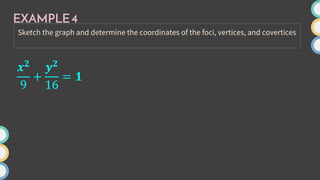
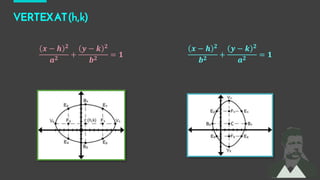
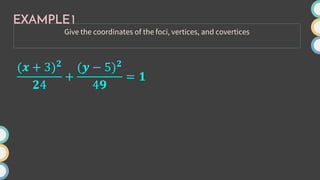
This document provides an overview of ellipses in pre-calculus. It defines an ellipse as a set of points where the sum of the distances from two fixed points (foci) is constant. Key properties of ellipses are described, including the relationship between the major axis, minor axis, foci, vertices, and covertices. Several examples are worked through, sketching ellipses from equations in standard form and determining characteristic points. Practice problems are provided to identify variables in equations and find standard forms.