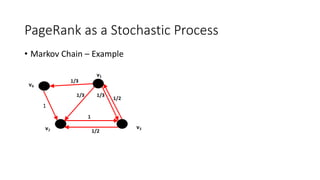
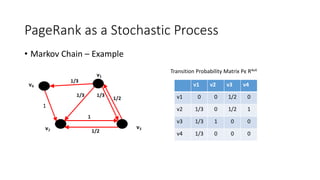
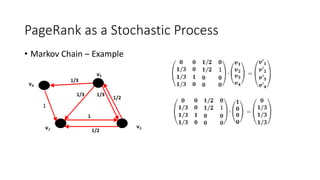
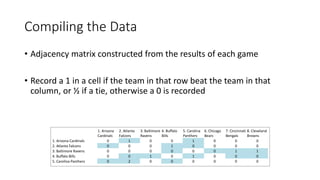
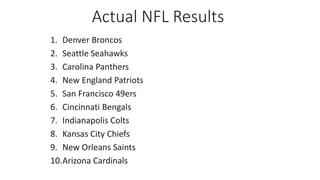
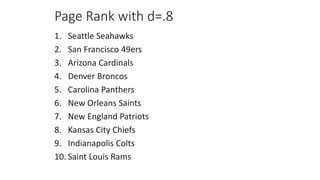
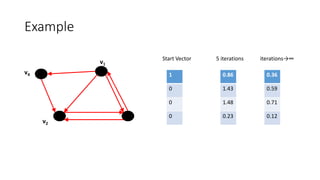
The PageRank algorithm was developed by Larry Page and Sergey Brin in 1996 to rank the importance of web pages. It measures a page's importance based on the number and quality of links to it, viewing the web as a directed graph. The algorithm models a random web surfer and calculates the probability of ending up on each page. It has since been refined by Google but remains an important factor in search engine results. Variations of PageRank can also be applied to other networks like ranking NFL teams based on game outcomes.

1. Page-Rank Algorithm
Brandon B, Abbie H, Billy K, Hannah S

2. Overview
• History and Background
• Importance and Problems
• Algorithm and Variations of it
• Our Application of PageRank

3. Background
• Mathematical equation designed to measure the importance of web
pages
• Developed in 1996 at Stanford University by Larry Page and Sergey
Brin, the founders of Google
• Started as a research project

4. Background
• PageRank is a trademark of Google
• PageRank algorithm has been patented
• Exact algorithm used today is unknown
• Algorithm is still tweaked each day to improve search
results

5. Background
• Algorithm is one of ~200 factors that determines the order web pages
are reported to the users
• Results are reported based on relevance to a search and overall importance
• Previously, internet search engines linked to pages that had the
highest keyword density

6. Problem with Previously Used Method
• Possible for websites to easily increase their rank in search results
• Did not take into account the relevancy of the results to the search,
therefore was not very useful

7. The Algorithm
• Measures a web page’s overall importance
• Importance of a page is based on the number of links into it from
other web pages
• Links can be viewed as votes
• Quality of the web pages linked into the page is taken into
consideration too

8. Web Pages as a Digraph
• Web pages and links can be viewed as a digraph
• Web pages are represented by vertices
• Links in are represented by arcs directed in
Videos
Books
Home
Football

9. Adjacency Matrix of Digraph
• After creating a digraph with the web pages and links, an adjacency
matrix is constructed
• Algorithm is then applied using this matrix and PageRank values are
determined
• On Google, pages are ranked from 1 to 10

10. Importance of PageRank
• PageRank is main factor used daily by Google to deliver the best
results to a Google search
• Can also be applied to other sets of data
• Many real-life applications of the algorithm are possible (i.e. ranking NFL
teams based on wins and losses)

11. Problems with the Algorithm
• Some websites look for a way to increase their own PageRank
• Called search engine optimization (SEO)
• Two specific examples of cheating:
• Google Bomb
• Link Farming

12. Google Bomb
• Occurs when a group of people conspire to increase PageRank
artificially by linking a particular word or phrase to the website
• Prevention: alter algorithm to rank pages by relevancy

13. Link Farming
• Linking without the thought of relevance of pages being linked
• i.e. a website with a collection of random links to other websites
• Prevention: alter calculations to filter out possible link farms

14. Real Life Examples of Cheating
• JC Penny (furniture)
• BMW German Car Sales Website
• Bing uses Google’s search engine ranking system to improve their
own

15. The Algorithm
• Construct a digraph with nodes representing pages
• Number of nodes = N
• W = NxN adjacency matrix where wij = 1 if there is a link from page i to page j
• wij = 0 if there is no link from i to j
• Degi is the out degree of node i, and D is the NxN diagonal matrix of deg
• so =
𝟏
𝑵
𝟏
𝟏
⋮
𝟏
=
𝟏
𝑵
𝟏
𝑵
⋮
𝟏
𝑵
is the starting vector with equal probabilities of each vertex

16. Example
v1
v2
v4
v3

17. Example
Adjacency Matrix
v1
v2
v4
v3
V1 V2 V3 V4
V1 0 1 1 1
V2 0 0 1 0
V3 1 1 0 0
V4 0 1 0 0

18. Example
Adjacency Matrix Transpose
v1
v2
v4
v3
V1 V2 V3 V4
V1 0 0 1 0
V2 1 0 1 1
V3 1 1 0 0
V4 1 0 0 0

19. Example
Adjacency Matrix Transpose/out degrees
v1
v2
v4
v3
V1 V2 V3 V4
V1 0 0 .5 0
V2 1/3 0 .5 1
V3 1/3 1 0 0
V4 1/3 0 0 0

20. Example
Start Vector
1
0
0
0
5 iterations
0.86
1.43
1.48
0.23
v1
v2
v4
iterations→∞
0.36
0.59
0.71
0.12

21. PageRank as a Stochastic Process
• Markov Chain
• Discrete-time stochastic process
• Consisting of N states and a transition probability matrix Pϵ RNxN
• At each step, we are in exactly one of the states

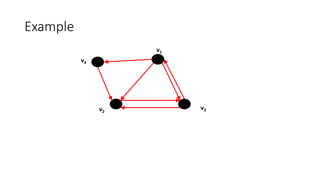
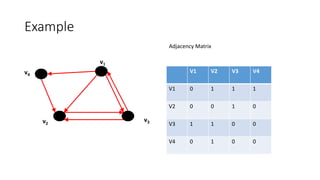
22. PageRank as a Stochastic Process
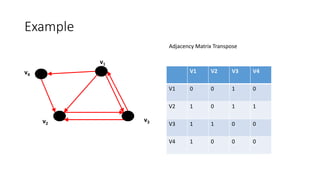
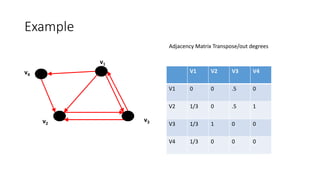
• Markov Chain - Transition Probability Matrix
• Each entry is in the interval [0, 1]
• Pij = probability of j being the next state, given we are currently in state i ,
for 1  i,j  n
• A stochastic matrix has non-negative entries and satisfies
• Each entry is known as a transition probability and depends only on the
current state i.

23. PageRank as a Stochastic Process
• Markov Chain – Example
1

24. PageRank as a Stochastic Process
• Markov Chain – Example
v1 v2 v3 v4
v1 0 0 1/2 0
v2 1/3 0 1/2 1
v3 1/3 1 0 0
v4 1/3 0 0 0
Transition Probability Matrix Pϵ R4x4
1

25. PageRank as a Stochastic Process
• Markov Chain – Example
1
1
1

26. PageRank as a Stochastic Process
• Markov Chain
• sk=Pk∙s0 , s is the state vector
• Does the process “settle down” and converge to a certain vector?

27. Linear Algebra
• What state vector should it converge to?
• Want a state vector, π, that satisfies PT∙π = π (i.e. PT∙π = 1 ∙ π)
• Recall definition: π is an eigenvector for eigenvalue λ = 1
• A stochastic matrix has 1 as its maximum eigenvalue
• This is the “Long term” or “steady state” vector
• This vector exists if the stochastic matrix is regular
• Some power of P has all non-zero entries.

28. Random Walk
• Random Walk
• Suppose you are at vertex (page) vi
• Randomly choose a vertex vj that vi is directed out to
• Transition to that vertex
• Probability of being at vj given at vi
• 0 if wij= 0 (no link from i to j)
• wij/degi if wij= 1 (link exists from i to j)
• Problems?
• Getting stuck at a vertex with no out degrees
• More generally: getting caught in an isolated cycle
• Non-regular matrix

29. Teleporting Random Walk
• Teleporting operation:
• The surfer jumps from a node to any other node in the Web graph,
e.g. type an address into URL bar
• The destination of a teleport operation is chosen uniformly at random for all
Web pages: 1/N

30. Teleporting Random Walk

31. Application of PageRank to the NFL
• Apply the algorithm to last year’s NFL regular season to achieve a
ranking of the NFL teams based on importance
• Vary the algorithm to see how the rankings would change
• Compare our results to the actual results of the season

32. Compiling the Data
• View each match up week by week, record the outcome of each
game.
• Teams = vertices, games played = directed arcs
• For teams A and B, if team A lost to team B an arc would be directed from A
to B in the digraph
• The in-degree of each vertex is the amount of games that team won,
so the out-degree of each vertex is the amount of games lost.
• Example of subgraph of the digraph.

33. Compiling the Data
• Adjacency matrix constructed from the results of each game
• Record a 1 in a cell if the team in that row beat the team in that
column, or ½ if a tie, otherwise a 0 is recorded
1. Arizona
Cardinals
2. Atlanta
Falcons
3. Baltimore
Ravens
4. Buffalo
Bills
5. Carolina
Panthers
6. Chicago
Bears
7. Cincinnati
Bengals
8. Cleveland
Browns
1. Arizona Cardinals 0 1 0 0 1 0 0 0
2. Atlanta Falcons 0 0 0 1 0 0 0 0
3. Baltimore Ravens 0 0 0 0 0 0 1 1
4. Buffalo Bills 0 0 1 0 1 0 0 0
5. Carolina Panthers 0 2 0 0 0 0 0 0

34. Actual NFL Results
1. Denver Broncos
2. Seattle Seahawks
3. Carolina Panthers
4. New England Patriots
5. San Francisco 49ers
6. Cincinnati Bengals
7. Indianapolis Colts
8. Kansas City Chiefs
9. New Orleans Saints
10.Arizona Cardinals

35. Page Rank with d=1
1. Seattle Seahawks
2. San Francisco 49ers
3. Arizona Cardinals
4. New Orleans Saints
5. Carolina Panthers
6. Denver Broncos
7. New England Patriots
8. Saint Louis Rams
9. Kansas City Chiefs
10. Indianapolis Colts

36. Page Rank with d=.8
1. Seattle Seahawks
2. San Francisco 49ers
3. Arizona Cardinals
4. Denver Broncos
5. Carolina Panthers
6. New Orleans Saints
7. New England Patriots
8. Kansas City Chiefs
9. Indianapolis Colts
10. Saint Louis Rams

37. Page Rank with d=.5
1. Seattle Seahawks
2. San Francisco 49ers
3. Denver Broncos
4. Carolina Panthers
5. New England Patriots
6. New Orleans Saints
7. Arizona Cardinals
8. Kansas City Chiefs
9. Indianapolis Colts
10. Philadelphia Eagles

38. Page Rank with d=.2
1. Seattle Seahawks
2. San Francisco 49ers
3. Denver Broncos
4. Carolina Panthers
5. New England Patriots
6. New Orleans Saints
7. Arizona Cardinals
8. Kansas City Chiefs
9. Indianapolis Colts
10. Philadelphia Eagles