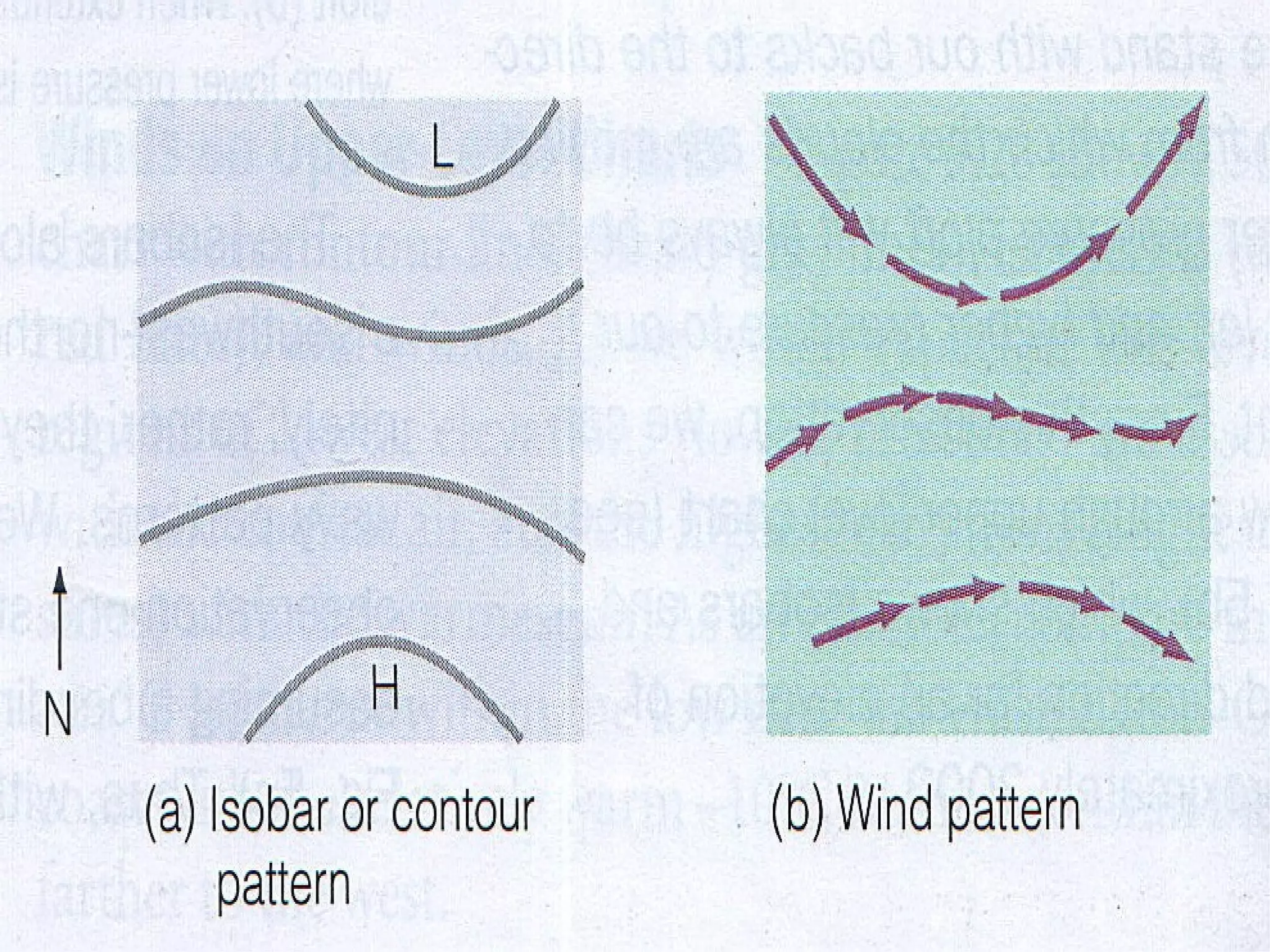
The document discusses geostrophic winds, which blow parallel to isobars due to a balance between the pressure gradient force and the Coriolis force. It provides an example calculation of geostrophic wind speed given latitude, isobar spacing, pressure difference, altitude, air density, and other variables. Specifically, it calculates a geostrophic wind speed of 59.4 knots (30.4 m/s) for conditions at 40°N latitude with a 200km isobar spacing and 4mb pressure difference.

1. GEOSTROPHIC WINDS

2.  Geo means earth and Strophic means
turning.
 Have a look on Figure 1 that shows a map of
Northern hemisphere.
 It shows horizontal pressure variations @
altitude 1km above earth surface.

4.  The isobars are evenly spaced and indicate a
constant pressure gradient force PGF
directed from south towards north as given by
an left arrow in the figure.
 Now what is PGF

5.  If there are isobars showing the horizontal
pressure difference change. If we compute
the amount of pressure change that occurs
over a given distance the PGF is given as:
difference in pressure
PGF= ____________________
distance

6.  Suppose there is an air parcel at position 1.
 The PGF acts immediately at position 1
upon the air parcel pushing it northward
towards low pressure.
 Now as the air moves the Coriolis force
deflects the air towards its right, curving its
path.

7.  The air parcel increases its speed at points
2, 3, 4 and with it the magnitude of the
Coriolis force also increases (as shown by the
longer arrows).
 This causes the bending of the wind more
and more towards its right.

8.  Atlast the wind speed increases to a point
where the Coriolis force just balances the
PGF (shown by point 5).
 Now the wind no longer accelerates as the
net force is zero.

9.  Here the wind flows in a straight path parallel
to the isobars at a constant speed.
 This flow of air is called Geostrophic wind.
 The figure also shows that geostrophic wind
blows in the Northern hemisphere with lower
pressure to its left and higher pressure to its
right

10.  When the air flow is purely geostrophic the
isobars are straight ,evenly spaced and the
wind speed is constant.
 In the atmosphere the isobars are hardly
straight or evenly spaced and the wind
changes its speed as it moves.

12.  The figure shows that a geostrophic wind flowing
parallel to the isobars is similar to the water in a
stream flowing parallel to its bank.
 At position 1 the wind is blowing at a low speed
& at position 2 the PGF increases and the wind
speed also increases.
 At position 2, where the wind sped is greater
the Coriolis force is greater and balances the
PGF

14.  The figure shows an isobaric chart.
 On this chart the geostrophic wind direction and
speed can be determined.
 If we know the geostrophic wind direction &
speed, we can estimate the orientation and
spacing of the isobars.
 Winds do not always blow in a straight line, they
frequently curve and change their direction.

15.  Above the friction level (500-1000) m above
the earth surface, the winds tend to blow
parallel to the isobars (contours).
 At any given latitude the speed of the
geostrophic wind is proportional to the
pressure gradient and is given as:
d
p
Vg
∆
≈

16.  Vg = geostrophic wind
 Δp = pressure difference between two places
 d = horizontal distance
 The equation shows that greater the pressure
gradient, stronger is the geostrophic wind.

17.  When we take a unit mass of moving air, the air
density (ρ) should be taken into account.
 The geosptrophic wind can now be written as:
d
p
Vg
∆
≈
ρ
1

18.  Mathematically Coriolis force is represented
as:
 Coriolis force = 2ΏVsinØ
a. Ώ = earth’s angular spin (constant factor)
b. V = wind speed
c. Ø = latitude

19.  At equator 0° sinØ= 0, at 30 ° sinØ= 0.5 and at
poles sinØ = 1.
 The balance between the Coriolis force and the
pressure gradient force is given as:
CF = PGF
2ΏVgsinØ =
d
p∆
ρ
1

20.  Solving for V the geostrophic wind is given as:
 If we combine (2Ώ) & (sinØ) by a single factor f
(Coriolis parameter), the expression can now be
written as:
d
p
Vg
∆
Ω
= .
sin2
1
φ
d
p
f
Vg
∆
≈ .
1


21. Compute the geostrophic wind???

22.  Wind is blowing parallel to the isobars in the
Northern hemisphere.
 Latitude = 40°N
 Isobar spacing = 200km
 Pressure difference = 4 mb
 Altitude (above sea level) = 5600 m
 Air temp. = -25°C
 Air density = 0.70 kg/m3

23.  Δp = 4 mb = 400 Newtons/m2
 d= 200 km = 200000 m
 Sin Ø= sin (40°) = 0.64
 ρ = 0.70 kg/m3
 2Ώ = 14.6 X10-5
radian/sec.

24.  Putting in eqn.
d
p
Vg
∆
Ω
= .
sin2
1
φ
.
10270.064.0106.14
400
55
×××××
= −gV
sec/6.30 mVg =

25.  OR 59.4 knots
 knots x 0.515 = meters/sec.

26.  Rate of earth’s rotation (Ώ) = 360° per day.
 Earth’s sidereal period of rotation =23h
56m
4.1s.
(86164 seconds)
 But we need (Ώ) in radians
 2π radians = 360° (where π=3.14)
 So (Ώ) = 2π radians /86164 sec=7.29x10-6
radian/sec.
 2 Ώ = 14.6x10-6
radian/sec