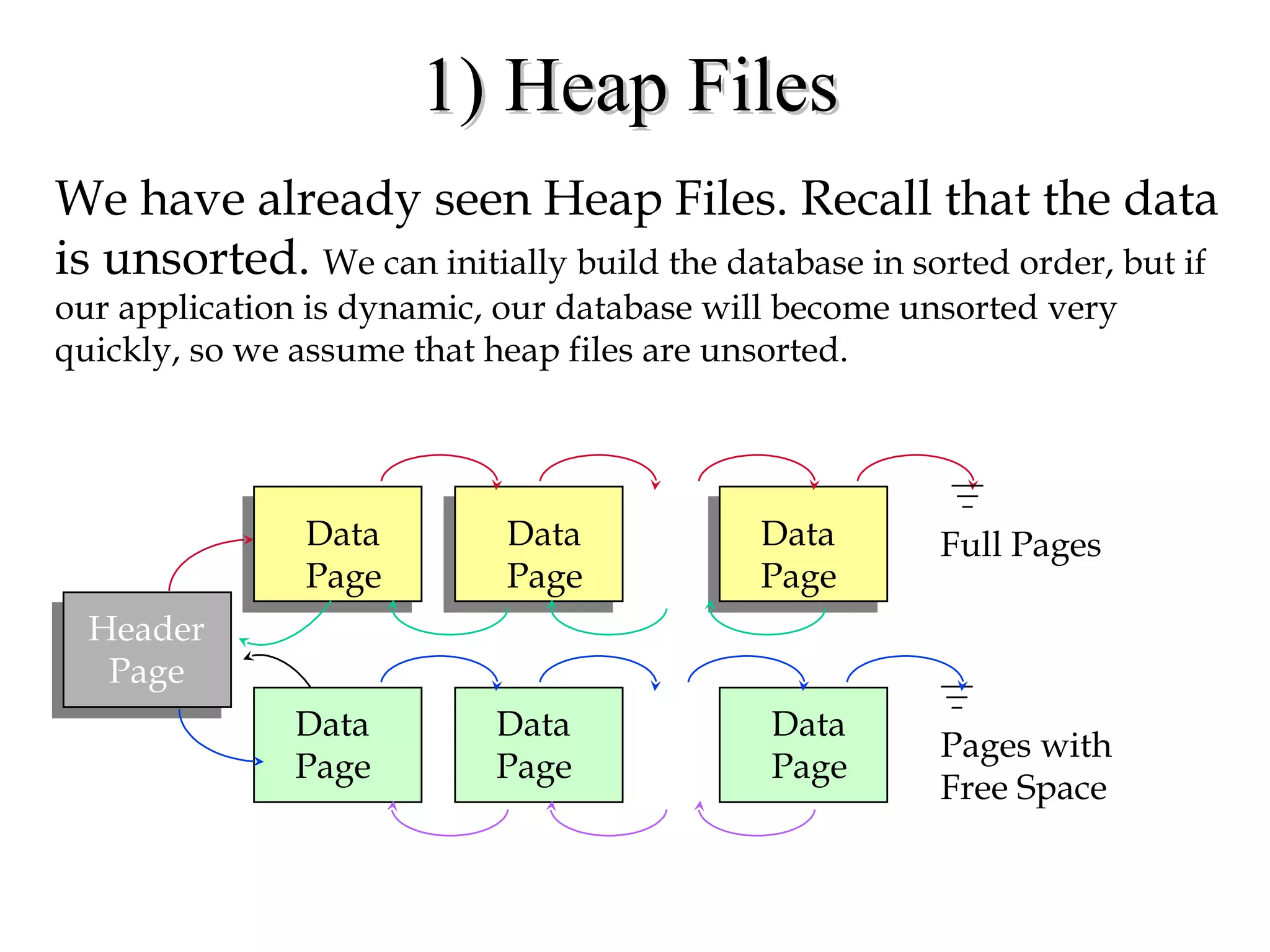
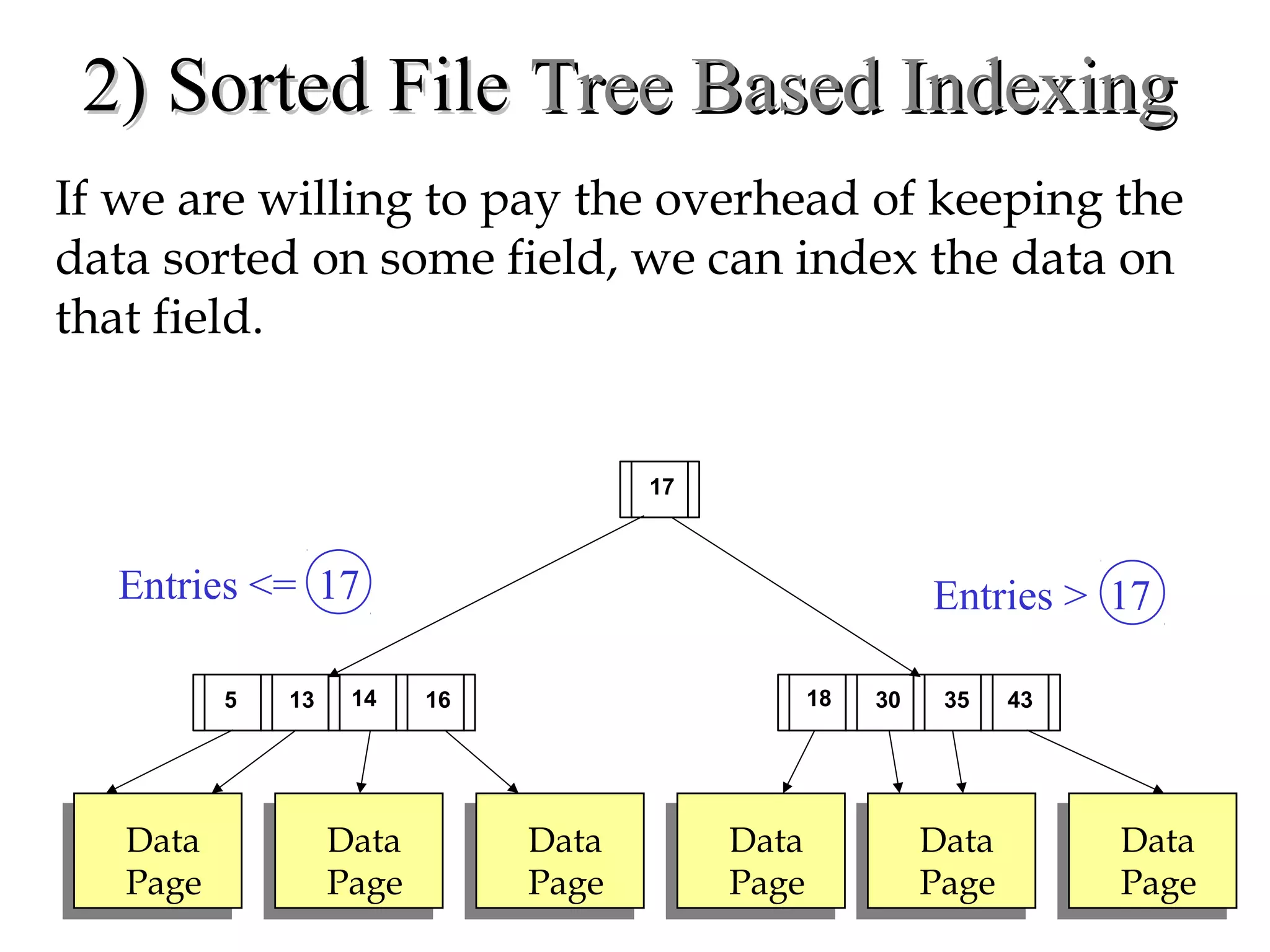
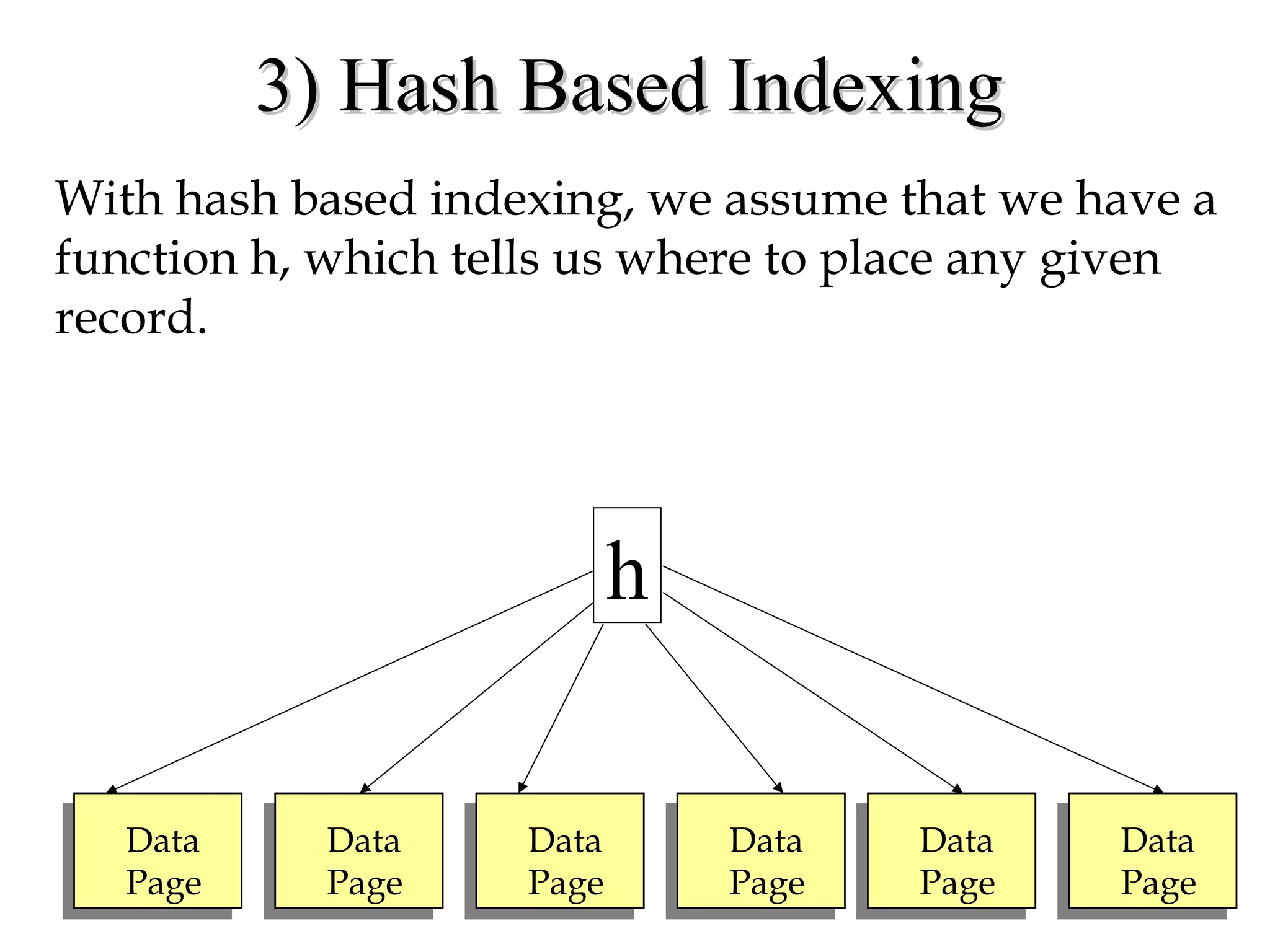
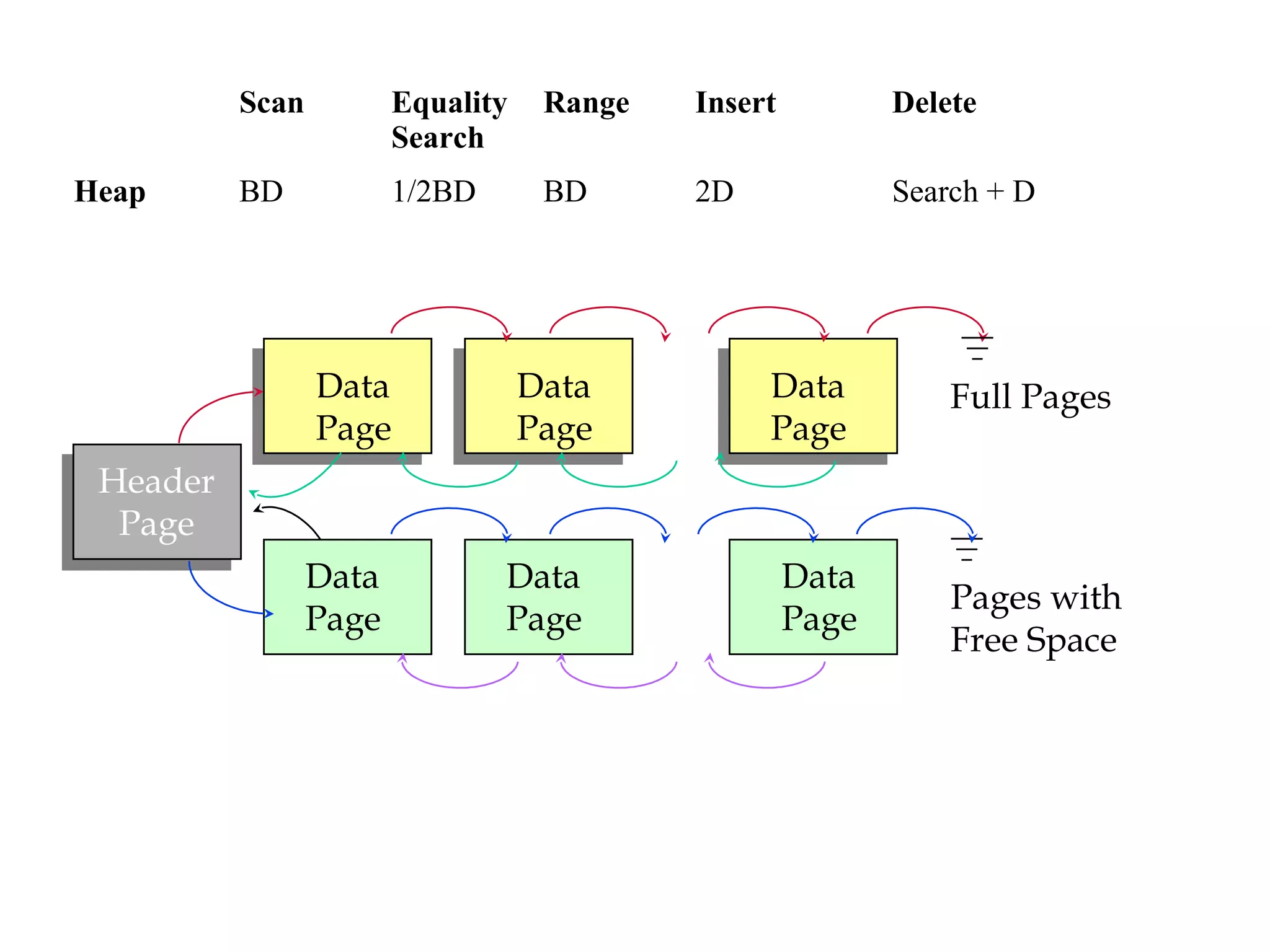
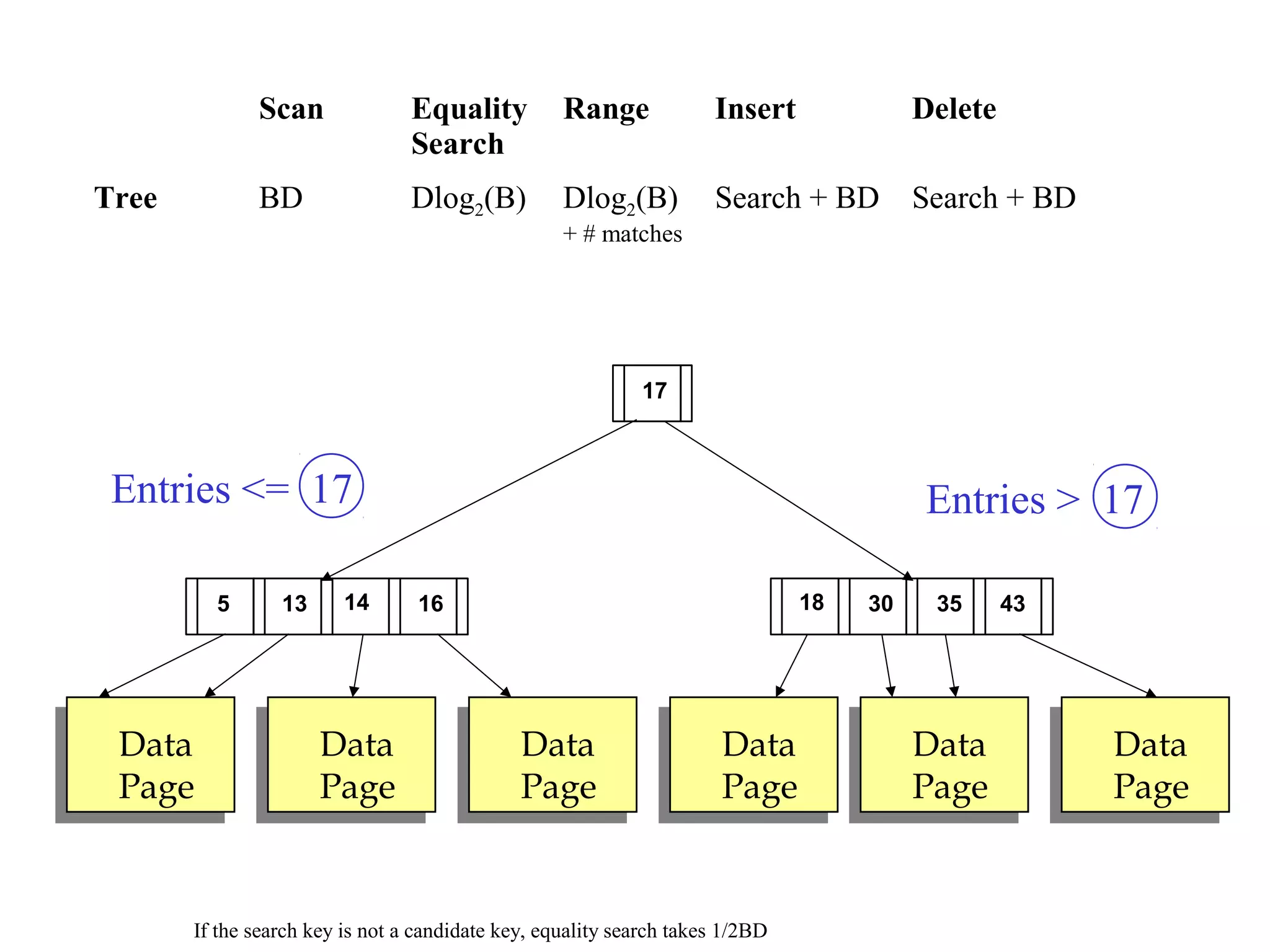
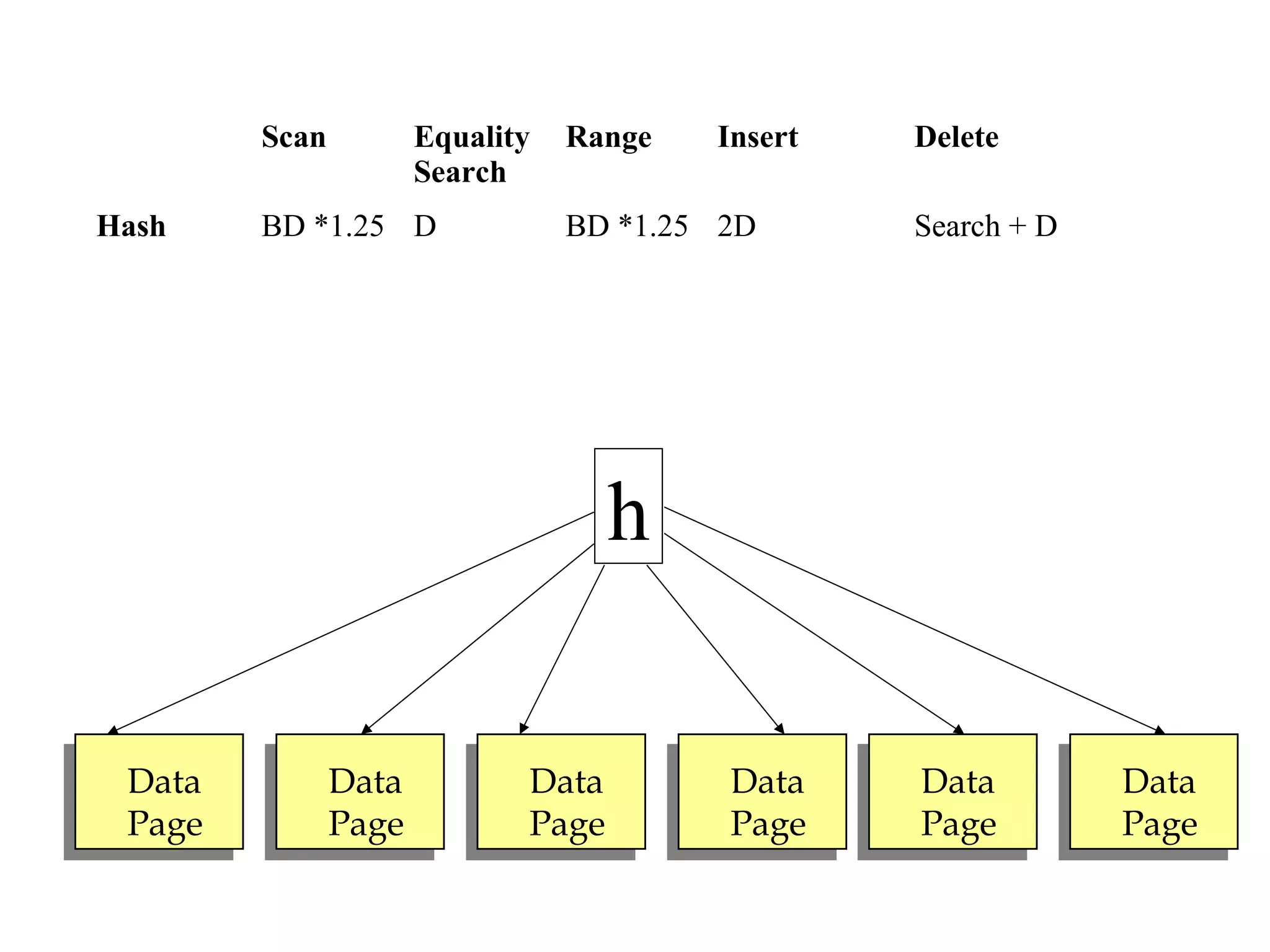
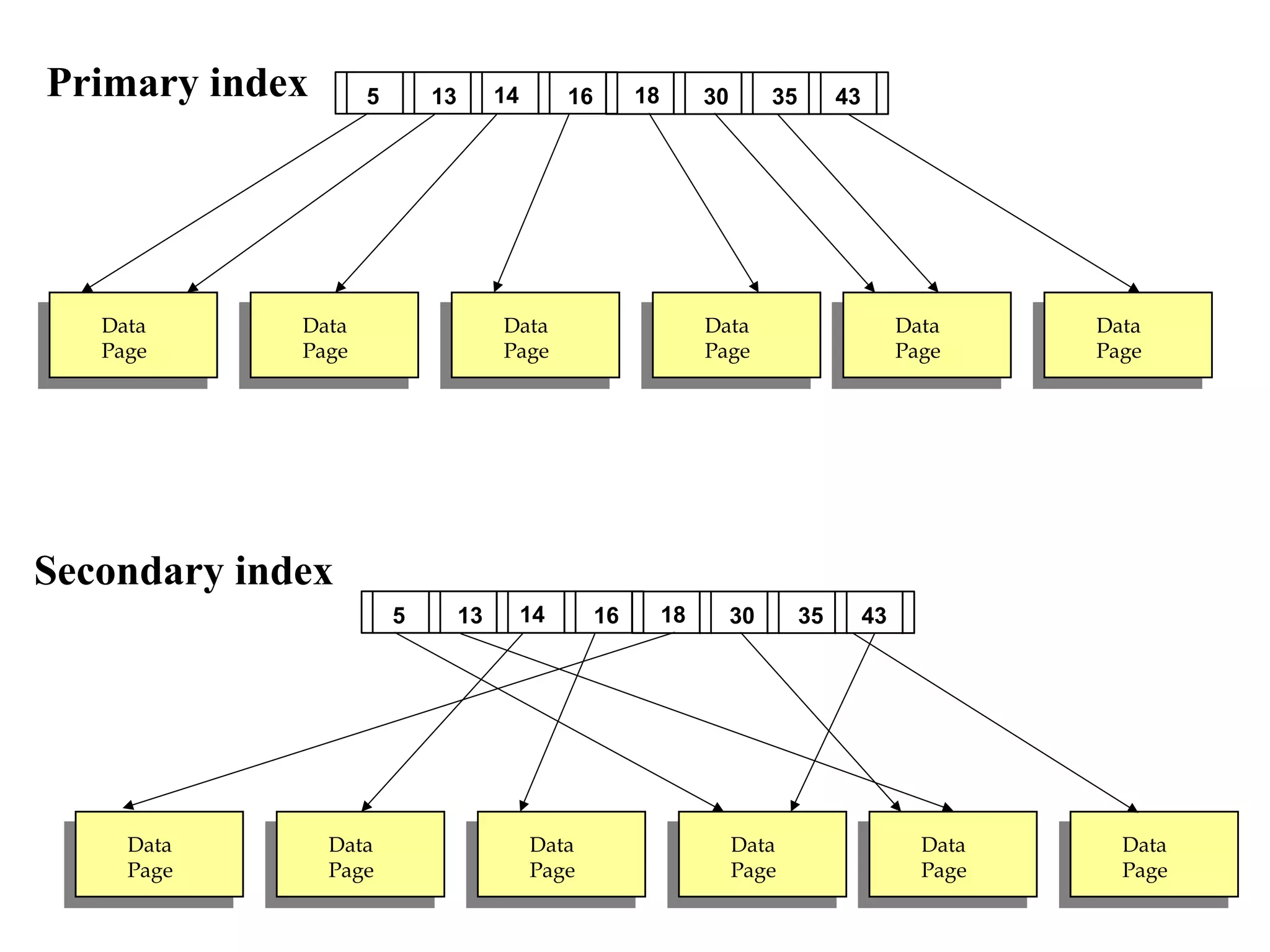
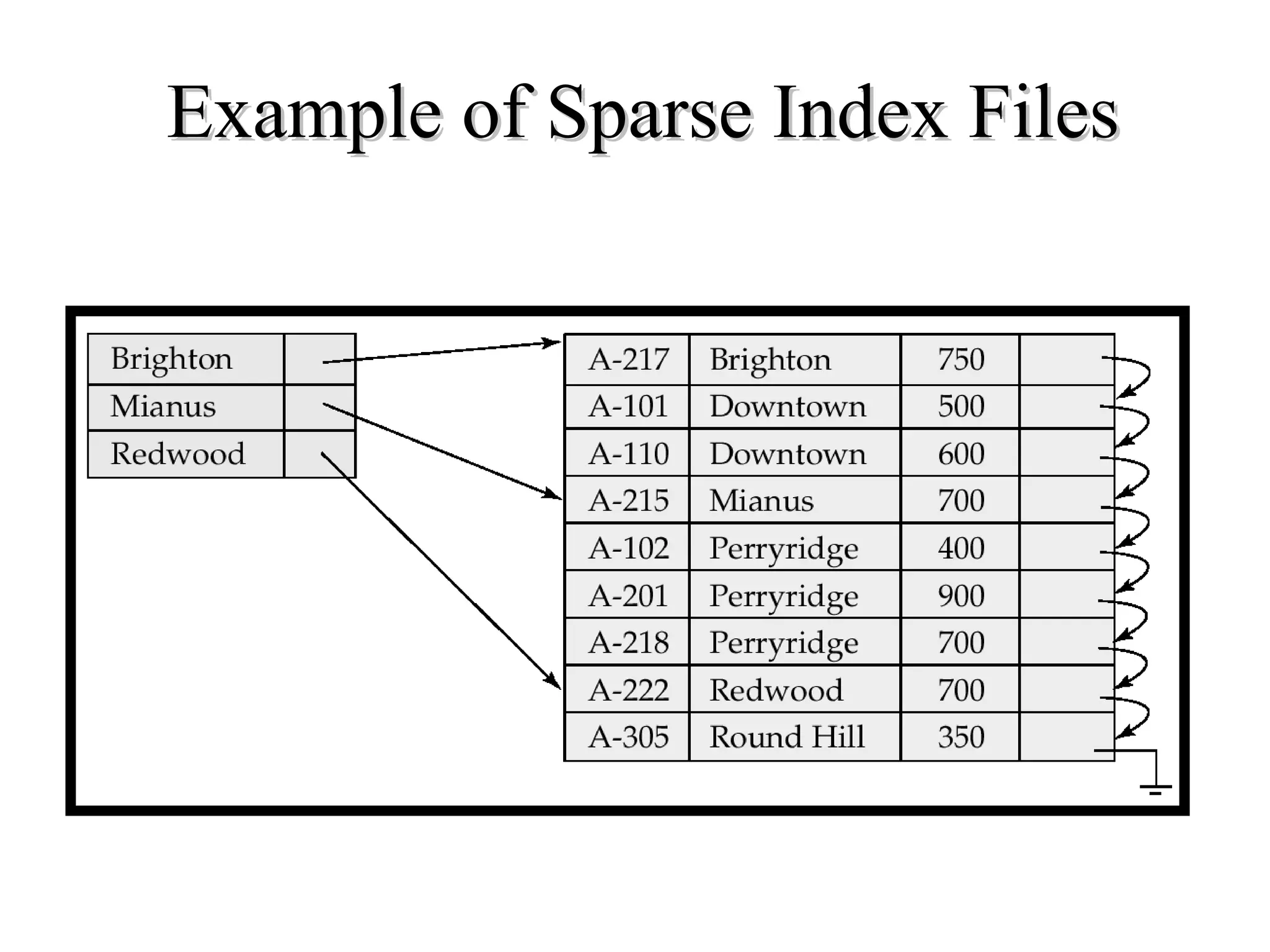
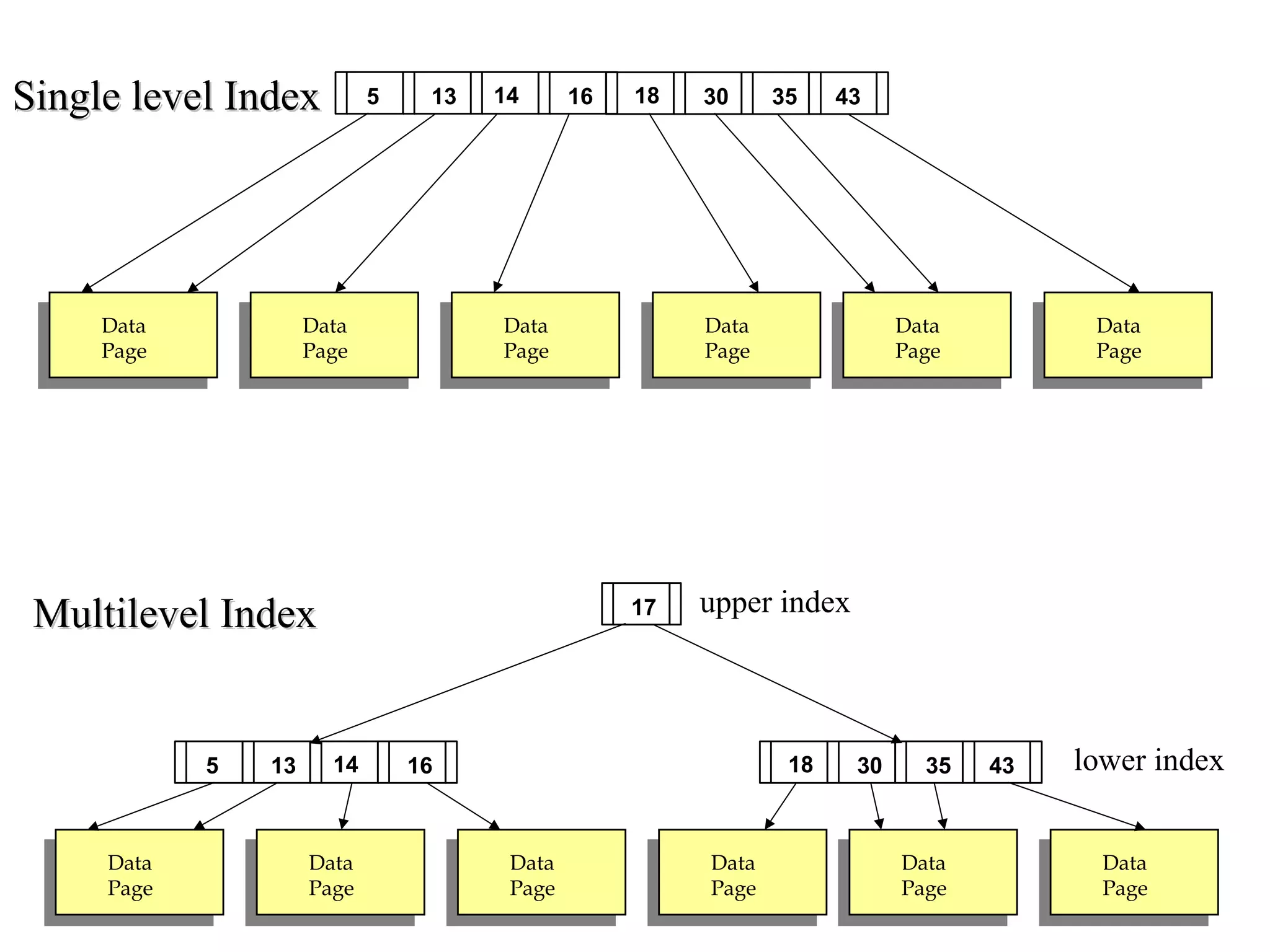
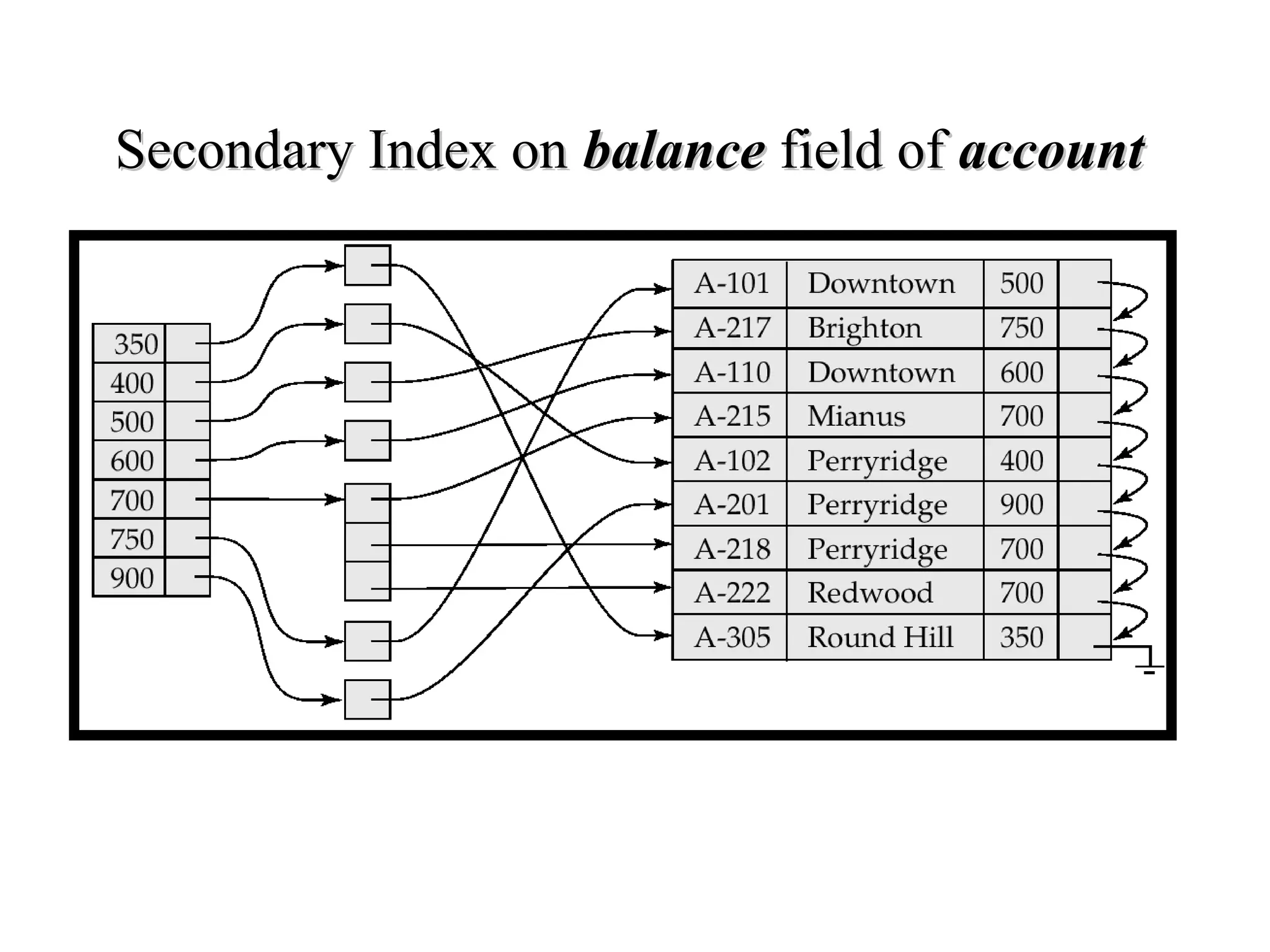
This document discusses different file organization and indexing techniques for databases. It begins by describing common operations like scans, searches, inserts and deletes. It then outlines three main file organization techniques: heap files, sorted files using tree-based indexing, and hash-based indexing. For each technique, it provides the cost in terms of disk I/O for the different operations. It also discusses concepts like primary and secondary indices, dense vs sparse indexing, and multilevel indexing. The document provides examples and diagrams to illustrate these concepts.

1. Chapter 8
File organization and Indices

2. File Organization and IndexingFile Organization and Indexing
Assume that we have a large amount of data in
our database which lives on a hard drive(s)
What are some of the things we might wish to
do with the data?
• Scan: Fetch all records from disk
• Equality search
• Range search
• Insert a record
• Delete a record
How expensive are these operations? (in terms of execution time)

3. How expensive are these operations?How expensive are these operations?
The cost of operations listed below depends on how
we organize data.
There are three main ways we could organize the
data
• Heap Files
• Sorted File (Tree Based Indexing)
• Hash Based Indexing
Scan/ Equality search/ Range selection/ Insert a record/ Delete a record

4. Important PointImportant Point
Data which is organized based on one field, may be difficult to search
based on a different field.
Consider a phone book. The data is well organized if you want to find
Eamonn Keogh’s phone number, suppose to want to find out whose
number 234-2342 is?
Informally, the attribute we are most interested in searching is called
the search key, or just key (we will formalize this notation later).
Note that the search key can be a combination of fields, for example
phone books are organized by <Last_name, First_name>
Unfortunately, the word key is overloaded in databases, the word key in this context, has
nothing to do with primary key, candidate key etc.

5. 1) Heap Files1) Heap Files
We have already seen Heap Files. Recall that the data
is unsorted. We can initially build the database in sorted order, but if
our application is dynamic, our database will become unsorted very
quickly, so we assume that heap files are unsorted.
Header
Page
Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
Pages with
Free Space
Full Pages

6. 2) Sorted File2) Sorted File Tree Based IndexingTree Based Indexing
If we are willing to pay the overhead of keeping the
data sorted on some field, we can index the data on
that field.
Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
30135 18
Entries <= 17 Entries > 17
14 16 35 43
17

7. 3) Hash Based Indexing3) Hash Based Indexing
With hash based indexing, we assume that we have a
function h, which tells us where to place any given
record.
Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
h

8. Cost Model for Our AnalysisCost Model for Our Analysis
We ignore CPU costs, for simplicity*:
– B: The number of data pages
– D: (Average) time to read or write disk page
– Measuring number of page I/O’s ignores gains of
pre-fetching a sequence of pages; thus, even I/O cost
is only approximated.
– Average-case analysis; based on several simplistic
assumptions.
*As we have already seen, a single disk access takes thousands of times longer than the CPU
time for most operations. Furthermore the trend is for this gap to increase.

9. Assumptions in Our AnalysisAssumptions in Our Analysis
• Heap Files:
– Equality selection on search key; exactly one match.
• Sorted Files:
– Files compacted after deletions.
• Indexes:
– Hash: No overflow buckets.
• 80% page occupancy => File size = 1.25 data size
• We only consider the cost of getting the right page(s)
into the buffer, we don’t consider how the records are
arranged in the buffer. Data
Page

10. Header
Page
Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
Pages with
Free Space
Full Pages
Scan Equality
Search
Range Insert Delete
Heap BD 1/2BD BD 2D Search + D

11. Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
30135 18
Entries <= 17 Entries > 17
14 16 35 43
17
Scan Equality
Search
Range Insert Delete
Tree BD Dlog2(B) Dlog2(B)
+ # matches
Search + BD Search + BD
If the search key is not a candidate key, equality search takes 1/2BD

12. Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
h
Scan Equality
Search
Range Insert Delete
Hash BD *1.25 D BD *1.25 2D Search + D

13. Scan Equality
Search
Range Insert Delete
Heap BD 1/2BD BD 2D Search + D
Tree BD Dlog2(B) Dlog2(B)
+ # matches
Search + BD Search + BD
Hash BD *1.25 D BD *1.25 2D Search + D
–B: The number of data pages
–D: (Average) time to read or write disk page
Comparison of all TechniquesComparison of all Techniques
• A heap is great if all you do is insert, delete and scan the data. But
if you have to do any kind of search, it is too slow.
• If you are only interest in equality searches, a hash index looks
very promising, although it does waste some space, disk space is
relatively cheap.
• If you need to do range search, use a tree.

14. Basic ConceptsBasic Concepts
• Indexing mechanisms used to speed up access to desired data.
– E.g., author catalog in library
• Search Key - attribute (or set of attributes) used to look up
records in a file.
• An index file consists of records (called index entries, or
data entries) of the form
• Index files are typically much smaller than the original file
• Two basic kinds of indices:
– Ordered indices: search keys are stored in sorted order (I.e tree based)
– Hash indices: search keys are distributed uniformly across “buckets”
using a “hash function”.
search-key pointer

15. Ordered IndicesOrdered Indices
• In an ordered index, (I.e tree based) index entries are stored sorted
on the search key value. E.g., author catalog in library.
• Primary index: in a sequentially ordered file, the index whose
search key specifies the sequential order of the file.
– Also called clustering index
– The search key of a primary index is usually but not necessarily the
primary key.
– Note that we can have at most one primary index
• Secondary index: an index whose search key specifies an order
different from the sequential order of the file. Also called
non-clustering index.
– We can have as many secondary indices as we like.
• Index-sequential file: ordered sequential file with a primary
index.

16. Primary index
Secondary index
Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
30135 1814 16 35 43
Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
30135 1814 16 35 43

17. Primary and Secondary IndicesPrimary and Secondary Indices
• Secondary indices have to be dense.
• Indices offer substantial benefits when searching for records.
• When a file is modified, every index on the file must be
updated, Updating indices imposes overhead on database
modification.
• Sequential scan using primary index is efficient, but a
sequential scan using a secondary index is expensive (probably
worse that no index at all).
– each record access may fetch a new block from disk

18. Index Update: DeletionIndex Update: Deletion
• If deleted record was the only record in the file with
its particular search-key value, the search-key is
deleted from the index also.
• Single-level index deletion:
– Dense indices – deletion of search-key is similar to file
record deletion.
– Sparse indices – if an entry for the search key exists in
the index, it is deleted by replacing the entry in the index
with the next search-key value in the file (in search-key
order). If the next search-key value already has an index
entry, the entry is deleted instead of being replaced.

19. Index Update: InsertionIndex Update: Insertion
• Single-level index insertion:
– Perform a lookup using the search-key value appearing in
the record to be inserted.
– Dense indices – if the search-key value does not appear in
the index, insert it.
– Sparse indices – if index stores an entry for each block of
the file, no change needs to be made to the index unless a
new block is created. In this case, the first search-key
value appearing in the new block is inserted into the
index.
• Multilevel insertion (as well as deletion) algorithms
are simple extensions of the single-level algorithms

20. Dense Index FilesDense Index Files
• Dense index — Index record appears for every
search-key value in the file.

21. Sparse Index FilesSparse Index Files
• Sparse Index: contains index records for only some search-key
values.
– Applicable when records are sequentially ordered on search-key
• To locate a record with search-key value K we:
– Find index record with largest search-key value < K
– Search file sequentially starting at the record to which the index record
points
• Less space and less maintenance overhead for insertions and
deletions.
• Generally slower than dense index for locating records.
• Good tradeoff: sparse index with an index entry for every
block in file, corresponding to least search-key value in the
block. (because bringing the block into memory is the greatest expense, and index size is
still small).
Phone book tab example

22. Example of Sparse Index FilesExample of Sparse Index Files

23. Multilevel IndexMultilevel Index
• If primary index does not fit in memory, access
becomes expensive.
• To reduce number of disk accesses to index records,
treat primary index kept on disk as a sequential file
and construct a sparse index on it.
– upper index – a sparse index of primary index
– lower index – the primary index file
• If even upper index is too large to fit in main memory,
yet another level of index can be created, and so on.
• Indices at all levels must be updated on insertion or
deletion from the file.

24. Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
30135 1814 16 35 43
17
Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
Data
Page
30135 1814 16 35 43
upper index
lower index
Multilevel IndexMultilevel Index
Single level IndexSingle level Index

25. Secondary IndicesSecondary Indices
• Frequently, one wants to find all the records whose values
in a certain field (which is not the search-key of the
primary index satisfy some condition.
– Example 1: In the account database stored sequentially by account
number, we may want to find all accounts in a particular branch
– Example 2: as above, but where we want to find all accounts with a
specified balance or range of balances
• We can have a secondary index with an index record for
each search-key value; index record points to a bucket that
contains pointers to all the actual records with that
particular search-key value.

26. Secondary Index onSecondary Index on balancebalance field offield of accountaccount