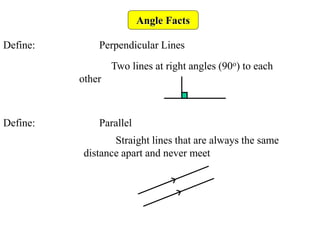
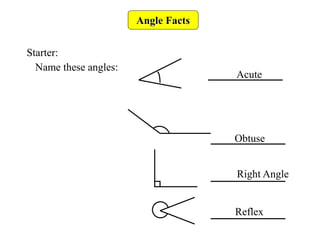
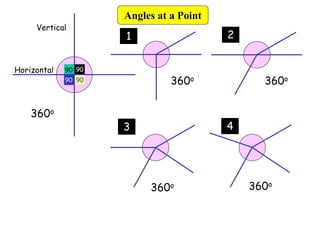
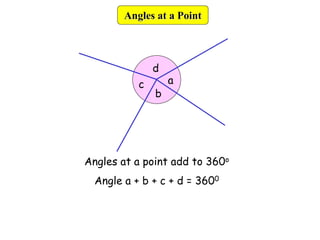
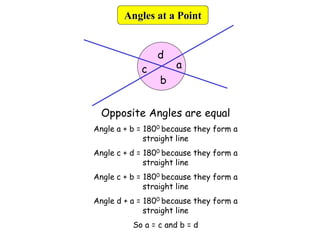
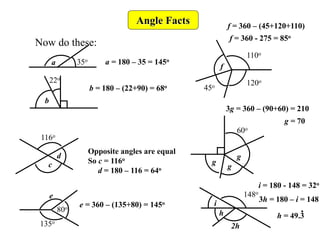
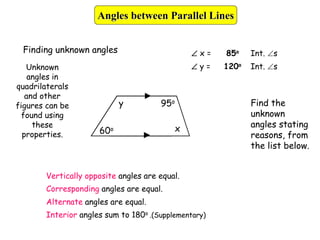
This document provides information about angle facts and properties. It defines key angle terms such as acute, obtuse, right, reflex, perpendicular, and parallel lines. It describes properties of angles including: angles at a point sum to 360 degrees; opposite angles are equal; corresponding angles are equal for parallel lines with a transversal; alternate angles are equal; and interior angles sum to 180 degrees. Examples are provided to demonstrate how to use these properties to determine unknown angle measures.