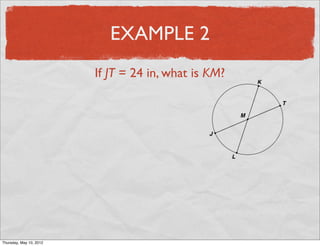
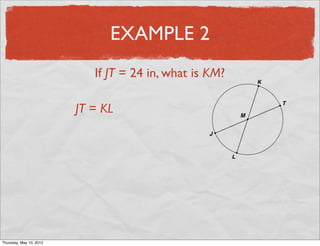
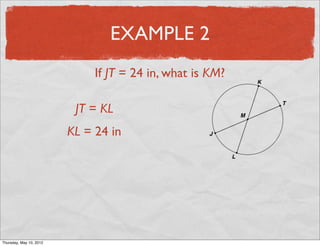
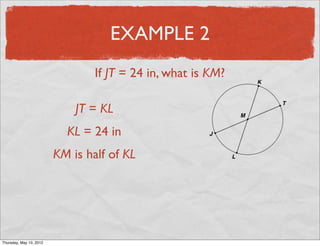
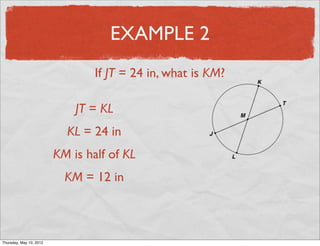
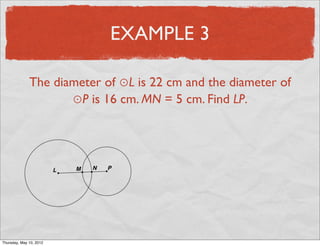
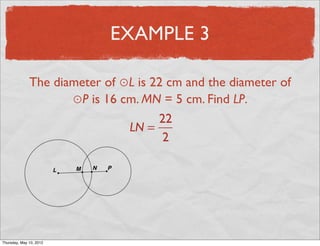
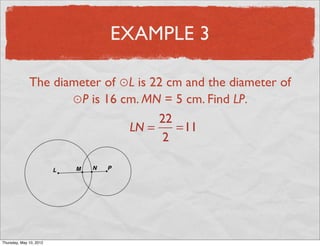
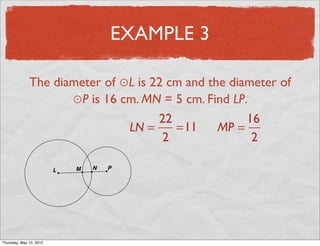
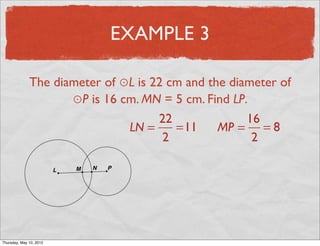
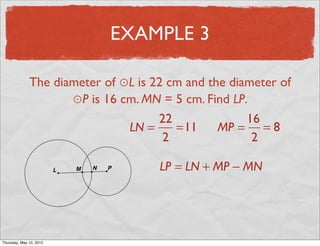
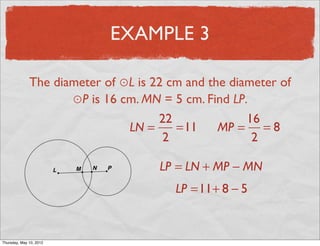
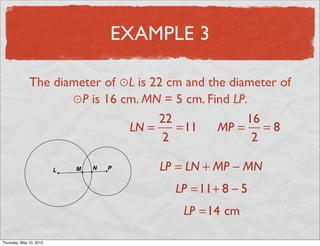
This document provides definitions and examples related to circles. It begins by defining key circle vocabulary terms like radius, diameter, chord, circumference, and pi. Examples are then provided to demonstrate finding parts of circles, calculating circumference, and solving problems involving radii, diameters and arc lengths. The final example finds the exact circumference of a circle given the length of its diameter. Overall, the document introduces fundamental concepts of circles and provides practice applying definitions and formulas to solve circle measurement problems.

1. CHAPTER 10
CIRCLES
Friday, May 11, 2012

2. SECTION 10-1
Circles and Circumference
Friday, May 11, 2012

3. ESSENTIAL QUESTIONS
How do you identify and use parts of circles?
How do you solve problems involving the
circumference of a circle?
Friday, May 11, 2012

4. VOCABULARY
1. Circle:
2. Center:
3. Radius:
4. Chord:
Friday, May 11, 2012

5. VOCABULARY
1. Circle: The set of points that are all the same
distance from a given point
2. Center:
3. Radius:
4. Chord:
Friday, May 11, 2012

6. VOCABULARY
1. Circle: The set of points that are all the same
distance from a given point
2. Center: The point that all of the points of a circle
are equidistant from
3. Radius:
4. Chord:
Friday, May 11, 2012

7. VOCABULARY
1. Circle: The set of points that are all the same
distance from a given point
2. Center: The point that all of the points of a circle
are equidistant from
3. Radius: A segment with one endpoint at the center
and the other on the edge of the circle; also the
distance from the center to the edge of the circle
4. Chord:
Friday, May 11, 2012

8. VOCABULARY
1. Circle: The set of points that are all the same
distance from a given point
2. Center: The point that all of the points of a circle
are equidistant from
3. Radius: A segment with one endpoint at the center
and the other on the edge of the circle; also the
distance from the center to the edge of the circle
4. Chord: A segment with both endpoints on the
edge of the circle
Friday, May 11, 2012

9. VOCABULARY
5. Diameter:
6. Congruent Circles:
7. Concentric Circles:
8. Circumference:
9. Pi (π):
Friday, May 11, 2012

10. VOCABULARY
5. Diameter: A special chord that passes through the
center of a circle; twice the length of the radius
6. Congruent Circles:
7. Concentric Circles:
8. Circumference:
9. Pi (π):
Friday, May 11, 2012

11. VOCABULARY
5. Diameter: A special chord that passes through the
center of a circle; twice the length of the radius
6. Congruent Circles: Two or more circles with
congruent radii
7. Concentric Circles:
8. Circumference:
9. Pi (π):
Friday, May 11, 2012

12. VOCABULARY
5. Diameter: A special chord that passes through the
center of a circle; twice the length of the radius
6. Congruent Circles: Two or more circles with
congruent radii
7. Concentric Circles: Coplanar circles with the same
center
8. Circumference:
9. Pi (π):
Friday, May 11, 2012

13. VOCABULARY
5. Diameter: A special chord that passes through the
center of a circle; twice the length of the radius
6. Congruent Circles: Two or more circles with
congruent radii
7. Concentric Circles: Coplanar circles with the same
center
8. Circumference: The distance around a circle
9. Pi (π):
Friday, May 11, 2012

14. VOCABULARY
5. Diameter: A special chord that passes through the
center of a circle; twice the length of the radius
6. Congruent Circles: Two or more circles with
congruent radii
7. Concentric Circles: Coplanar circles with the same
center
8. Circumference: The distance around a circle
9. Pi (π): The irrational number found from the ratio
of circumference to the diameter
Friday, May 11, 2012

15. VOCABULARY
10. Inscribed:
11. Circumscribed:
Friday, May 11, 2012

16. VOCABULARY
10. Inscribed: A polygon inside a circle where all of
the vertices of the polygon are on the circle
11. Circumscribed:
Friday, May 11, 2012

17. VOCABULARY
10. Inscribed: A polygon inside a circle where all of
the vertices of the polygon are on the circle
11. Circumscribed: A circle that is around a polygon
that is inscribed
Friday, May 11, 2012

18. EXAMPLE 1
a. Name the circle
b. Identify a radius
c. Identify a chord d. Name the diameter
Friday, May 11, 2012

19. EXAMPLE 1
a. Name the circle
Circle C or ⊙C
b. Identify a radius
c. Identify a chord d. Name the diameter
Friday, May 11, 2012

20. EXAMPLE 1
a. Name the circle
Circle C or ⊙C
b. Identify a radius
AC or CD
c. Identify a chord d. Name the diameter
Friday, May 11, 2012

21. EXAMPLE 1
a. Name the circle
Circle C or ⊙C
b. Identify a radius
AC or CD
c. Identify a chord d. Name the diameter
EB
Friday, May 11, 2012

22. EXAMPLE 1
a. Name the circle
Circle C or ⊙C
b. Identify a radius
AC or CD
c. Identify a chord d. Name the diameter
EB AD
Friday, May 11, 2012

23. EXAMPLE 2
If JT = 24 in, what is KM?
Friday, May 11, 2012

24. EXAMPLE 2
If JT = 24 in, what is KM?
JT = KL
Friday, May 11, 2012

25. EXAMPLE 2
If JT = 24 in, what is KM?
JT = KL
KL = 24 in
Friday, May 11, 2012

26. EXAMPLE 2
If JT = 24 in, what is KM?
JT = KL
KL = 24 in
KM is half of KL
Friday, May 11, 2012

27. EXAMPLE 2
If JT = 24 in, what is KM?
JT = KL
KL = 24 in
KM is half of KL
KM = 12 in
Friday, May 11, 2012

28. EXAMPLE 3
The diameter of ⊙L is 22 cm and the diameter of
⊙P is 16 cm. MN = 5 cm. Find LP.
Friday, May 11, 2012

29. EXAMPLE 3
The diameter of ⊙L is 22 cm and the diameter of
⊙P is 16 cm. MN = 5 cm. Find LP.
22
LN =
2
Friday, May 11, 2012

30. EXAMPLE 3
The diameter of ⊙L is 22 cm and the diameter of
⊙P is 16 cm. MN = 5 cm. Find LP.
22
LN = =11
2
Friday, May 11, 2012

31. EXAMPLE 3
The diameter of ⊙L is 22 cm and the diameter of
⊙P is 16 cm. MN = 5 cm. Find LP.
22 16
LN = =11 MP =
2 2
Friday, May 11, 2012

32. EXAMPLE 3
The diameter of ⊙L is 22 cm and the diameter of
⊙P is 16 cm. MN = 5 cm. Find LP.
22 16
LN = =11 MP = = 8
2 2
Friday, May 11, 2012

33. EXAMPLE 3
The diameter of ⊙L is 22 cm and the diameter of
⊙P is 16 cm. MN = 5 cm. Find LP.
22 16
LN = =11 MP = = 8
2 2
LP = LN + MP − MN
Friday, May 11, 2012

34. EXAMPLE 3
The diameter of ⊙L is 22 cm and the diameter of
⊙P is 16 cm. MN = 5 cm. Find LP.
22 16
LN = =11 MP = = 8
2 2
LP = LN + MP − MN
LP =11+ 8 − 5
Friday, May 11, 2012

35. EXAMPLE 3
The diameter of ⊙L is 22 cm and the diameter of
⊙P is 16 cm. MN = 5 cm. Find LP.
22 16
LN = =11 MP = = 8
2 2
LP = LN + MP − MN
LP =11+ 8 − 5
LP =14 cm
Friday, May 11, 2012

36. EXAMPLE 4
Find the diameter and radius of a circle to the nearest
hundredth if the circumference of the circle is 65.4 feet.
Friday, May 11, 2012

37. EXAMPLE 4
Find the diameter and radius of a circle to the nearest
hundredth if the circumference of the circle is 65.4 feet.
C = πd
Friday, May 11, 2012

38. EXAMPLE 4
Find the diameter and radius of a circle to the nearest
hundredth if the circumference of the circle is 65.4 feet.
C = πd
65.4 = π d
Friday, May 11, 2012

39. EXAMPLE 4
Find the diameter and radius of a circle to the nearest
hundredth if the circumference of the circle is 65.4 feet.
C = πd
65.4 = π d
π π
Friday, May 11, 2012

40. EXAMPLE 4
Find the diameter and radius of a circle to the nearest
hundredth if the circumference of the circle is 65.4 feet.
C = πd
65.4 = π d
π π
d ≈ 20.82 ft
Friday, May 11, 2012

41. EXAMPLE 4
Find the diameter and radius of a circle to the nearest
hundredth if the circumference of the circle is 65.4 feet.
C = πd
65.4 = π d
π π
d ≈ 20.82 ft
r ≈10.41 ft
Friday, May 11, 2012

42. EXAMPLE 5
Find the exact circumference of ⊙R.
BF = 3 2
Friday, May 11, 2012

43. EXAMPLE 5
Find the exact circumference of ⊙R.
BF = 3 2
(BR) + (RF ) = (BF )
2 2 2
Friday, May 11, 2012

44. EXAMPLE 5
Find the exact circumference of ⊙R.
BF = 3 2
(BR) + (RF ) = (BF )
2 2 2
r + r = (3 2 )
2 2 2
Friday, May 11, 2012

45. EXAMPLE 5
Find the exact circumference of ⊙R.
BF = 3 2
(BR) + (RF ) = (BF )
2 2 2
r + r = (3 2 )
2 2 2
2r = (3 2 )
2 2
Friday, May 11, 2012

46. EXAMPLE 5
Find the exact circumference of ⊙R.
BF = 3 2
(BR) + (RF ) = (BF )
2 2 2
r + r = (3 2 )
2 2 2
2r = (3 2 )
2 2
2r = 9(2)
2
Friday, May 11, 2012

47. EXAMPLE 5
Find the exact circumference of ⊙R.
BF = 3 2
(BR) + (RF ) = (BF )
2 2 2
r + r = (3 2 )
2 2 2
2r = (3 2 )
2 2
2r = 9(2)
2
r =9
2
Friday, May 11, 2012

48. EXAMPLE 5
Find the exact circumference of ⊙R.
BF = 3 2
(BR) + (RF ) = (BF )
2 2 2
r = 9
2
r + r = (3 2 )
2 2 2
2r = (3 2 )
2 2
2r = 9(2)
2
r =9
2
Friday, May 11, 2012

49. EXAMPLE 5
Find the exact circumference of ⊙R.
BF = 3 2
(BR) + (RF ) = (BF )
2 2 2
r = 9
2
r + r = (3 2 )
2 2 2
r =3
2r = (3 2 )
2 2
2r = 9(2)
2
r =9
2
Friday, May 11, 2012

50. EXAMPLE 5
Find the exact circumference of ⊙R.
BF = 3 2
(BR) + (RF ) = (BF )
2 2 2
r = 9
2
r + r = (3 2 )
2 2 2
r =3
2r = (3 2 )
2 2
C = 2π r
2r = 9(2)
2
r =9
2
Friday, May 11, 2012

51. EXAMPLE 5
Find the exact circumference of ⊙R.
BF = 3 2
(BR) + (RF ) = (BF )
2 2 2
r = 9
2
r + r = (3 2 )
2 2 2
r =3
2r = (3 2 )
2 2
C = 2π r
2r = 9(2)
2
C = 2π (3)
r =9
2
Friday, May 11, 2012

52. EXAMPLE 5
Find the exact circumference of ⊙R.
BF = 3 2
(BR) + (RF ) = (BF )
2 2 2
r = 9
2
r + r = (3 2 )
2 2 2
r =3
2r = (3 2 )
2 2
C = 2π r
2r = 9(2)
2
C = 2π (3)
r =9
2
C = 6π
Friday, May 11, 2012

53. CHECK YOUR
UNDERSTANDING
p. 687 #1-9
Friday, May 11, 2012

54. PROBLEM SET
Friday, May 11, 2012

55. PROBLEM SET
p. 687 #11-41 odd, 71
“We don't know who we are until we see what
we can do.” - Martha Grimes
Friday, May 11, 2012