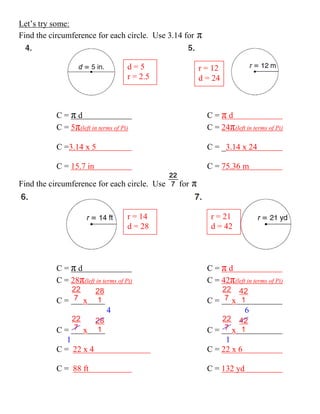
This document is a lesson on circles that defines key terms like circle, radius, diameter, chord, and pi. It provides examples of using these terms to name parts of a circle diagram and calculate circumference using formulas like C=πd. Students are asked to work problems finding circumference for various circles using both π and 3.14.

1. Name ________________________________ Date _____________________
Mrs. Labuski & Mrs. Rooney Period _____ Lesson 10-5 Circle
VOCABULARY DEFINITION EXAMPLE
Set of all points in a plane
A
that are the same distance
CIRCLE
from a given point called the
center.
The center is the name of Circle A
the circle
A line segment with one
RADIUS endpoint at the center of the
(radii) circle and the other endpoint
on the circle
A line segment that passes
DIAMETER
through the center of the
circle and has both
endpoints on the circle
A line segment that does
CHORD
NOT pass through the center
of the circle but has both
endpoints on the circle
Use the picture on the right to answer the following questions:
1. Name the circle ____Circle X____________________
2. Name the two diameters of the circle. WY and VZ
3. Name the four radii of the circle. WX (XW), VX (XV), ZX (XZ) ,YX (XY)
4. Name the chord of the circle. YZ

2. VOCABULARY DEFINITION EXAMPLE
The ratio of the
PI circumference to the
π diameter.
π = 3.14 or
The distance around
CIRCUMFERENCE the edge of a circle.
Formula: C= πd
What does π mean?
Take the cookie and a licorice lace.
Measure the distance around the edge (circumference) of the cookie with the
licorice lace.
Cut off any extra licorice.
Now lay the licorice across the diameter of the cookie.
Cut off any extra licorice.
Lay the licorice across the diameter of the cookie again.
Cut off any extra licorice.
Lay the licorice across the diameter of the cookie again.
Cut off any extra licorice.
How many pieces do you have? ___________
How many diameters equal one circumference? ___________
How do we represent this ratio between the diameter and the circumference? _____
To find the circumference of a large object, we can use the formula: ____________.
Find the diameter and multiply it by π

3. Let’s try some:
Find the circumference for each circle. Use 3.14 for π
d=5 r = 12
r = 2.5 d = 24
C=πd C=πd
C = 5π(left in terms of Pi) C = 24π(left in terms of Pi)
C =3.14 x 5 C = _3.14 x 24
C = 15.7 in C = 75.36 m
Find the circumference for each circle. Use for π
r = 14 r = 21
d = 28 d = 42
C=πd C=πd
C = 28π(left in terms of Pi) C = 42π(left in terms of Pi)
C= x C= x
4 6
C= x C= x
1 1
C = 22 x 4 C = 22 x 6
C = 88 ft C = 132 yd

4. Name ________________________________ Date _____________________
Mrs. Labuski & Mrs. Rooney Period _____ Lesson 10-5 Circle
VOCABULARY DEFINITION EXAMPLE
A
CIRCLE
RADIUS
(radii)
DIAMETER
CHORD
Use the picture on the right to answer the following questions:
1. Name the circle ________________________
2. Name the two diameters of the circle. _________________
3. Name the four radii of the circle. _____________________
4. Name the chord of the circle._________________________

5. VOCABULARY DEFINITION EXAMPLE
PI
π
CIRCUMFERENCE
What does π mean?
Take the cookie and a licorice lace.
Measure the distance around the edge (circumference) of the cookie with the
licorice lace.
Cut off any extra licorice.
Now lay the licorice across the diameter of the cookie.
Cut off any extra licorice.
Lay the licorice across the diameter of the cookie again.
Cut off any extra licorice.
Lay the licorice across the diameter of the cookie again.
Cut off any extra licorice.
How many pieces do you have? ___________
How many diameters equal one circumference? ___________
How do we represent this ratio between the diameter and the circumference? _____
To find the circumference of a large object, we can use the formula: ____________.
Find the diameter and multiply it by π

6. Let’s try some:
Find the circumference for each circle. Use 3.14 for π
C=πd C = _______________
C = _______________ C = _______________
C = _______________ C = _______________
Find the circumference for each circle. Use for π
C=πd C = _______________
C = _______________ C = _______________
C = _______________ C = _______________