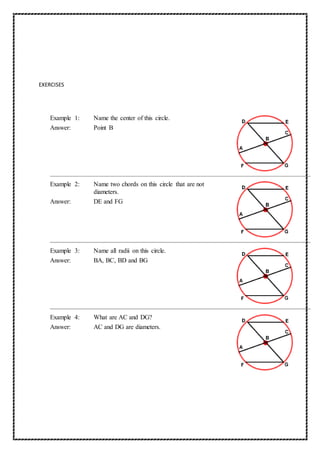
The document discusses circles, defining them as sets of points equidistant from a center point. It describes key circle terms like diameter, radius, chord, and circumference. Formulas are provided relating circumference to diameter using pi, diameter to radius, and area to radius. Examples demonstrate calculating circumference from diameter, diameter from circumference, and area from radius using the formulas. The document aims to define and explain key geometric concepts relating to circles through definitions, explanations, and example calculations.

1. CIRCLES
SUBMITTED BY
KAVITHA.C.KURUP,
REG NO:13304005
MATHEMATICS

2. Introduction
The word "circle" derives from the Greek κίρκος (kirkos), itself a metathesis of the Homeric Greek κρίκος
(krikos), meaning "hoop" or "ring".[2] The origins of the words "ci rcus" and "circuit" are closely related.
The circle has been known since before the beginning of recorded history. Natural circles would have
been observed, such as the Moon, Sun, and a short plant stalk blowing in the wind on sand, which forms
a circle shape in the sand. The circle is the basis for the wheel, which, with related inventions such as
gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped
inspire the development of geometry, astronomy, and calculus.
Early science, particularly geometry and astrology and astronomy, was connected to the divine for most
medieval scholars, and many believed that there was something intrinsically "divine" or "perfect" that
could be found in circles.[3][4]

3. CIRCLES
A circle is a simple shape of Euclidean geometry that is the set of all points in a plane that are at a given
distance from a given point, the centre. The distance between any of the points and the centre is called
the radius. It can also be defined as the locus of a point equidistant from a fixed point.
A circle is a simple closed curve which divides the plane into two regions: an interior and an exterior. In
everyday use, the term "circle" may be used interchangeably to refer to either the boundary of the
figure, or to the whole figure including its interior; in strict technical usage, the circle is the former and
the latter is called a disk.
A circle can be defined as the curve traced out by a point that moves so that its distance from a given
point is constant.
 The distance across a circle through the center is called the diameter. A
real-world example of diameter is a 9-inch plate.
 The radius of a circle is the distance from the center of a circle to any
point on the circle. If you place two radii end-to-end in a circle, you
would have the same length as one diameter. Thus, the diameter of a
circle is twice as long as the radius.

4. We can look at a pizza pie to find real-world examples of diameter and radius.
Look at the pizza to the right which has been sliced into 8 equal parts through
its center. A radius is formed by making a straight cut from the center to a point
on the circle. A straight cut made from a point on the circle, continuing through
its center to another point on the circle, is a diameter. As you can see, a circle
has many different radii and diameters, each passing through its center.
 A chord is a line segment that joins two points on a curve. In geometry,
a chord is often used to describe a line segment joining two endpoints
that lie on a circle. The circle to the right contains chord AB. If this circle
was a pizza pie, you could cut off a piece of pizza along chord AB. By
cutting along chord AB, you are cutting off a segment of pizza that
includes this chord.
 A circle has many different chords. Some chords pass through the center and some do not. A
chord that passes through the center is called a diameter.
 It turns out that a diameter of a circle is the longest chord of that circle since it passes through the
center. A diameter satisfies the definition of a chord, however, a chord is not necessarily a
diameter. This is because every diameter passes through the center of a circle, but some chords do
not pass through the center. Thus, it can be stated, every diameter is a chord, but not every chord
is a diameter.

5. EXERCISES
Example 1: Name the center of this circle.
Answer: Point B
Example 2: Name two chords on this circle that are not
diameters.
Answer: DE and FG
Example 3: Name all radii on this circle.
Answer: BA, BC, BD and BG
Example 4: What are AC and DG?
Answer: AC and DG are diameters.

6. Example 5: If DG is 5 inches long, then how long is DB?
Solution: The diameter of a circle is twice as long as the
radius.
5 inches ÷ 2 = 2.5 inches
Answer: The length of DB is 2.5 inches
Circumference of a Circle
A circle is a shape with all points the same distance from the center. It is named by the center. The circle to
the left is called circle A since the center is at point A. If you measure the distance around a circle and
divide it by the distance across the circle through the center, you will always come close to a particular
value, depending upon the accuracy of your measurement. This value is approximately
3.14159265358979323846... We use the Greek letter (pronounced Pi) to represent this value. The number
goes on forever. However, using computers, has been calculated to over 1 trillion digits past the
decimal point.
The distance around a circle is called the circumference. The distance across a
circle through the center is called the diameter. is the ratio of the
circumference of a circle to the diameter. Thus, for any circle, if you divide the
circumference by the diameter, you get a value close to . This relationship is
expressed in the following formula:
where is circumference and is diameter. You can test this formula at home with a round dinner
plate. If you measure the circumference and the diameter of the plate and then divide by , your
quotient should come close to . Another way to write this formula is: where · means
multiply. This second formula is commonly used in problems where the diameter is given and the
circumference is not known
The radius of a circle is the distance from the center of a circle to any point on the circle. If you place
two radii end-to-end in a circle, you would have the same length as one diameter. Thus, the diameter
of a circle is twice as long as the radius. This relationship is expressed in the following formula:
, where is the diameter and is the radius.

7. EXAMPLES
Example 1: The radius of a circle is 2 inches. What is the diameter?
Solution:
= 2 · (2 in)
= 4 in
Example 2: The diameter of a circle is 3 centimeters. What is the
circumference?
Solution:
= 3.14 · (3 cm)
= 9.42 cm
Example
3:
The radius of a circle is 2 inches. What is the circumference?
Solution:
= 2 · (2 in)
= 4 in
= 3.14 · (4 in)
= 12.56 in
Example
4:
The circumference of a circle is 15.7 centimeters. What is the
diameter?
Solution:
15.7 cm = 3.14 ·
15.7 cm ÷ 3.14 =
= 15.7 cm ÷ 3.14
= 5 cm

8. Area of a Circle
The area of a circle is the number of square units inside that circle. If each square in
the circle to the left has an area of 1 cm2, you could count the total number of
squares to get the area of this circle. Thus, if there were a total of 28.26 squares,
the area of this circle would be 28.26 cm2 However, it is easier to use one of the
following formulas:
or
where is the area, and is the radius. Let's look at some examples involving the
area of a circle. In each of the three examples below, we will use = 3.14 in our
calculations.
Example 1: The radius of a circle is 3 inches. What is the area?
Solution:
= 3.14 · (3 in) · (3 in)
= 3.14 · (9 in2)
= 28.26 in2
=
2 (2
in
)
=
4
in