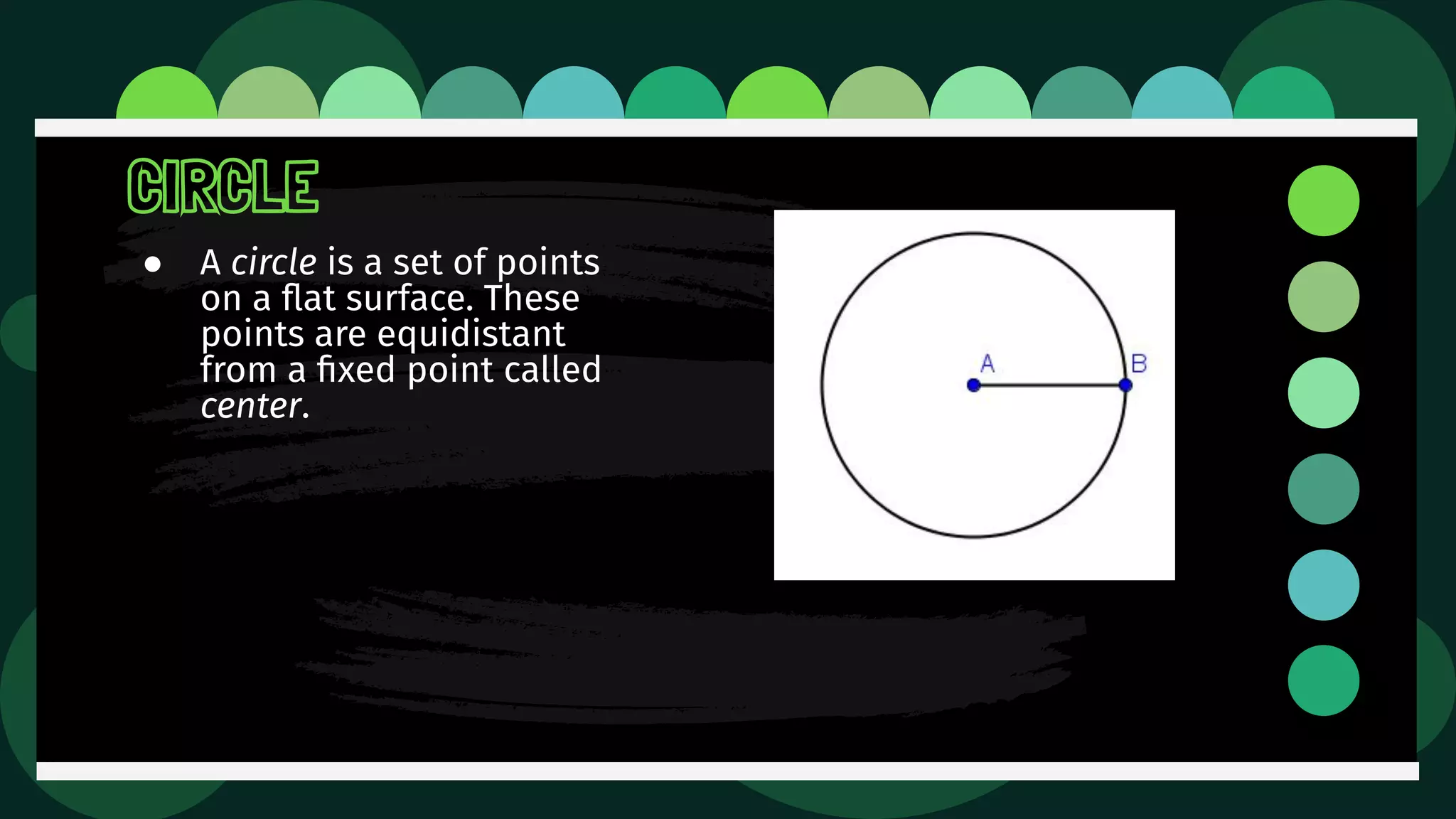
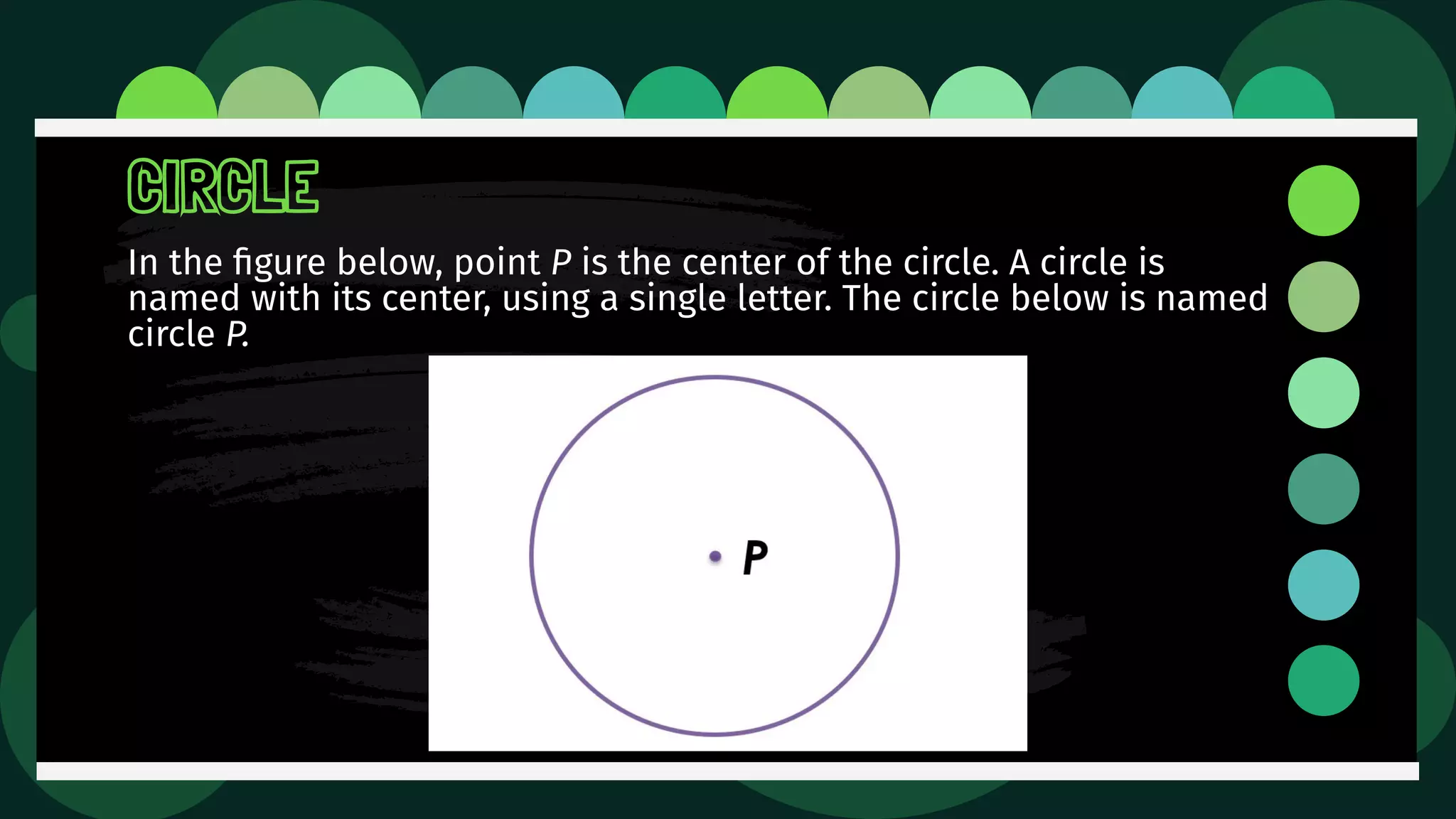
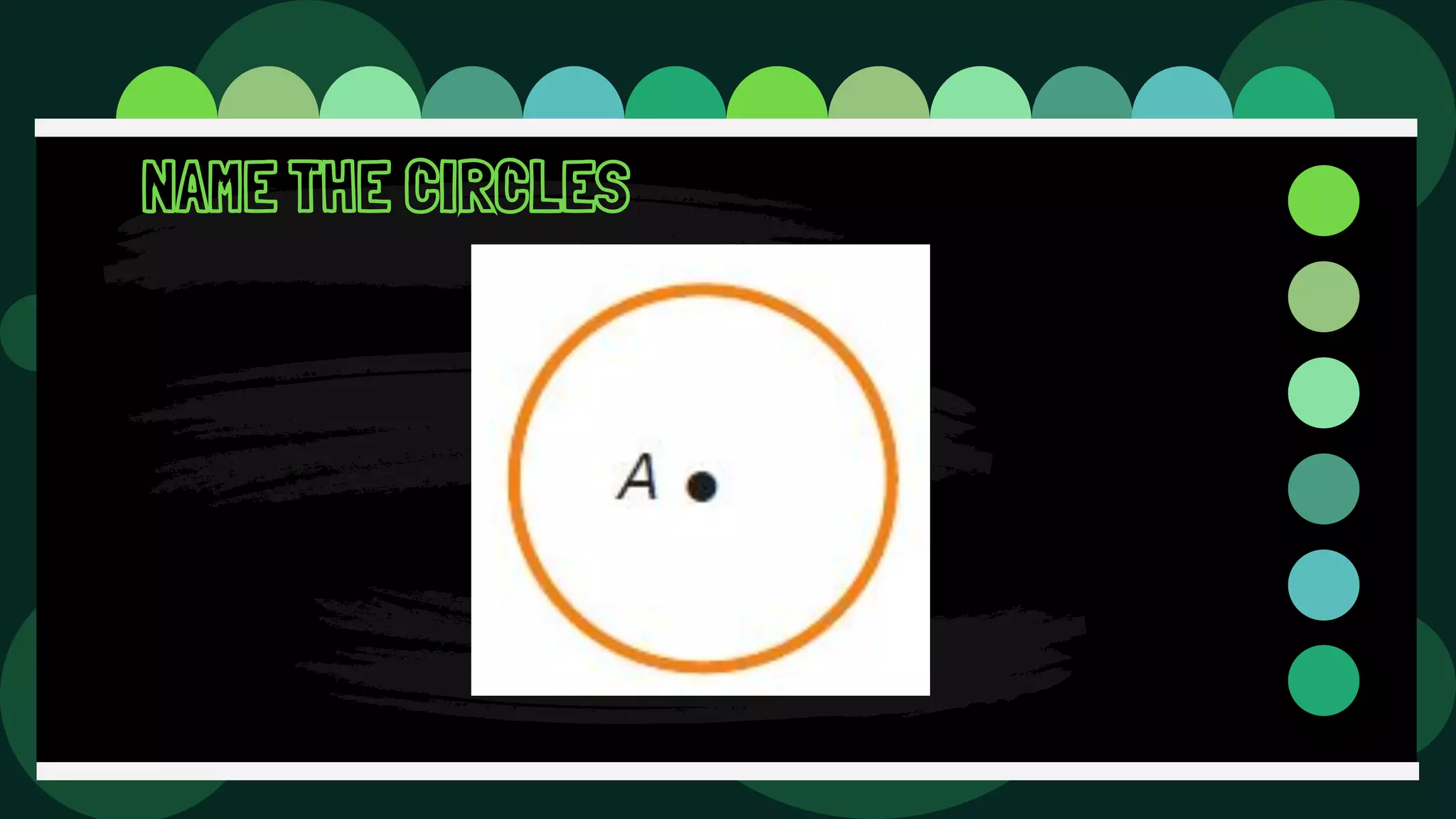
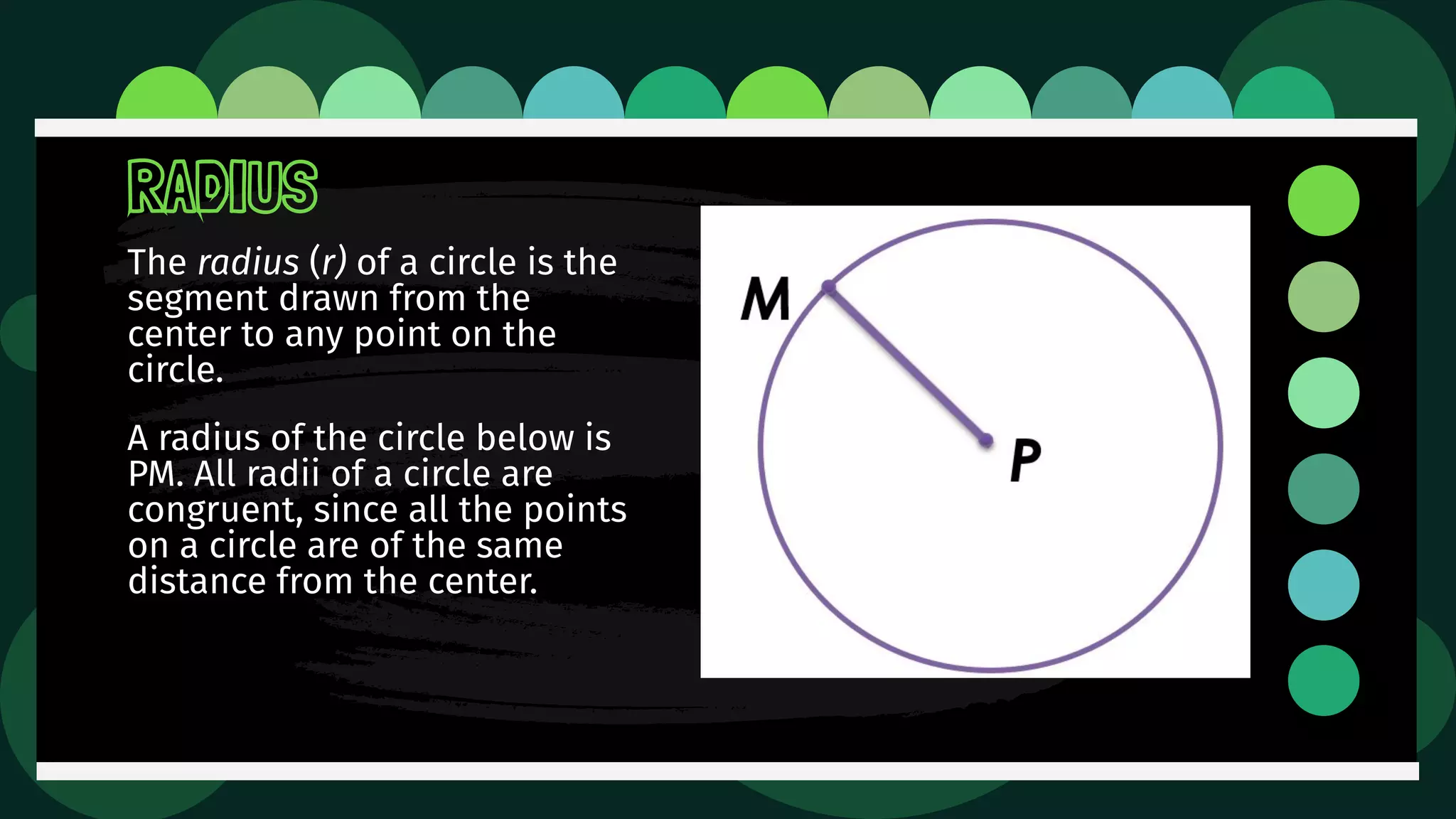
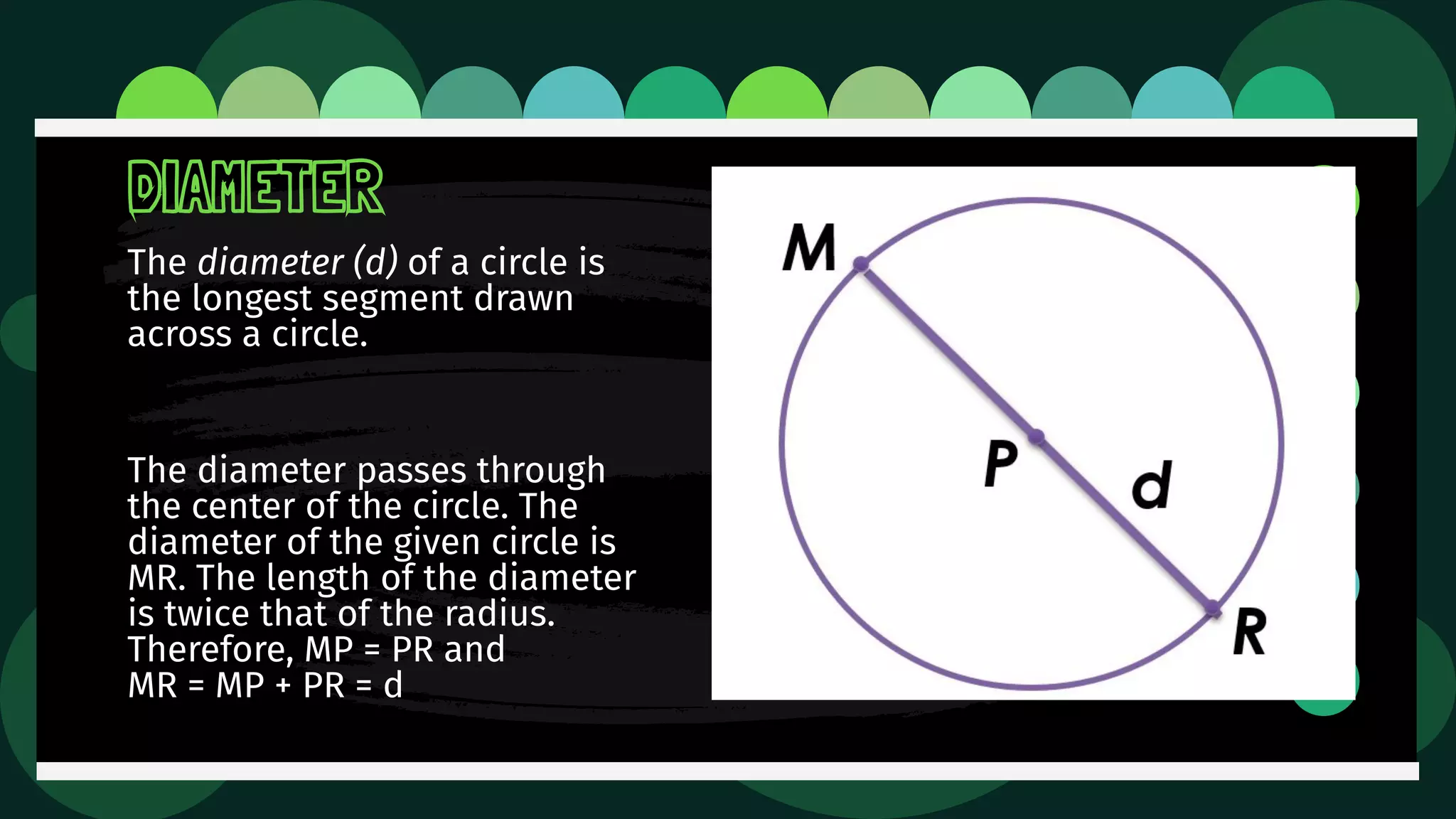
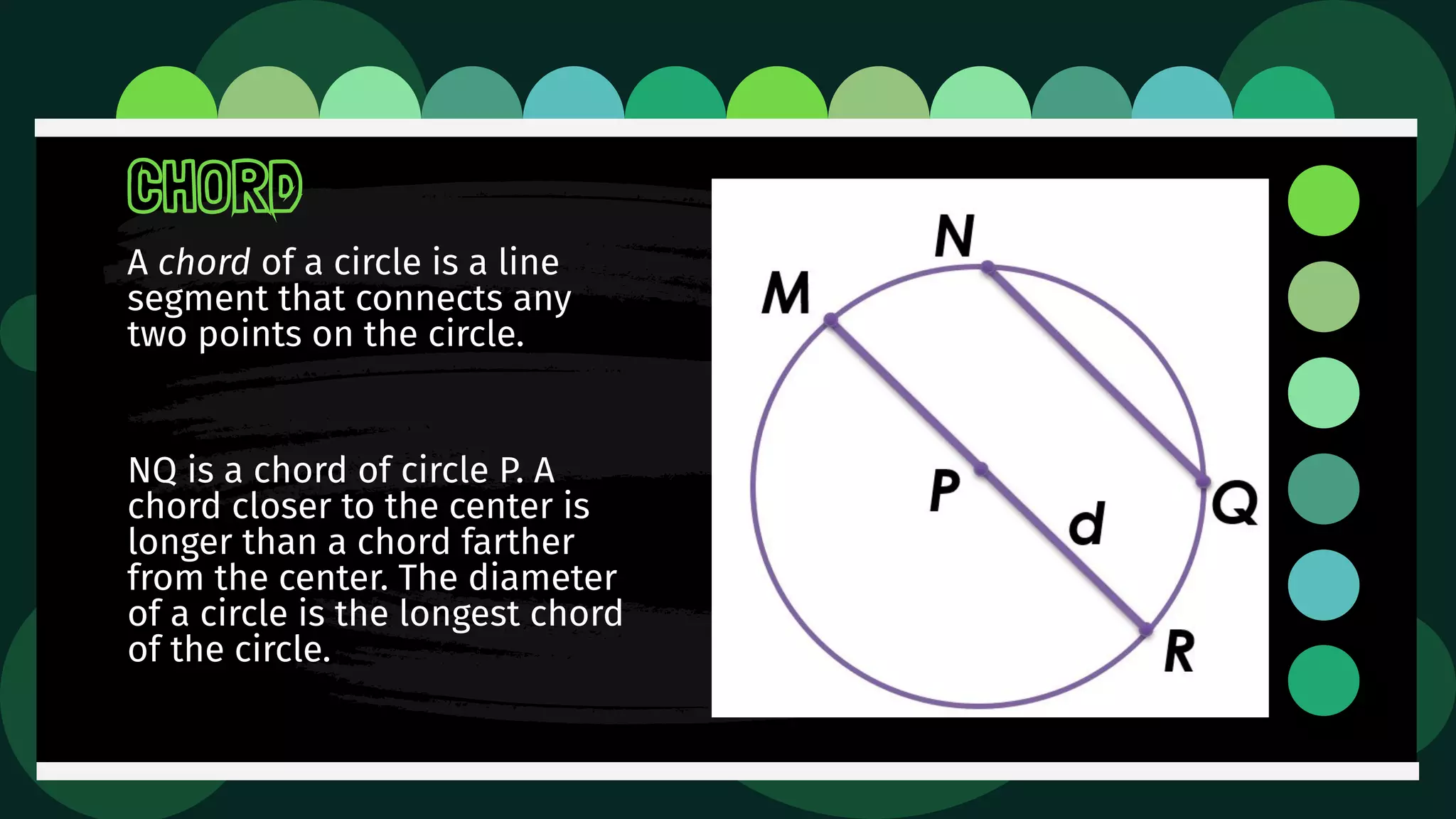
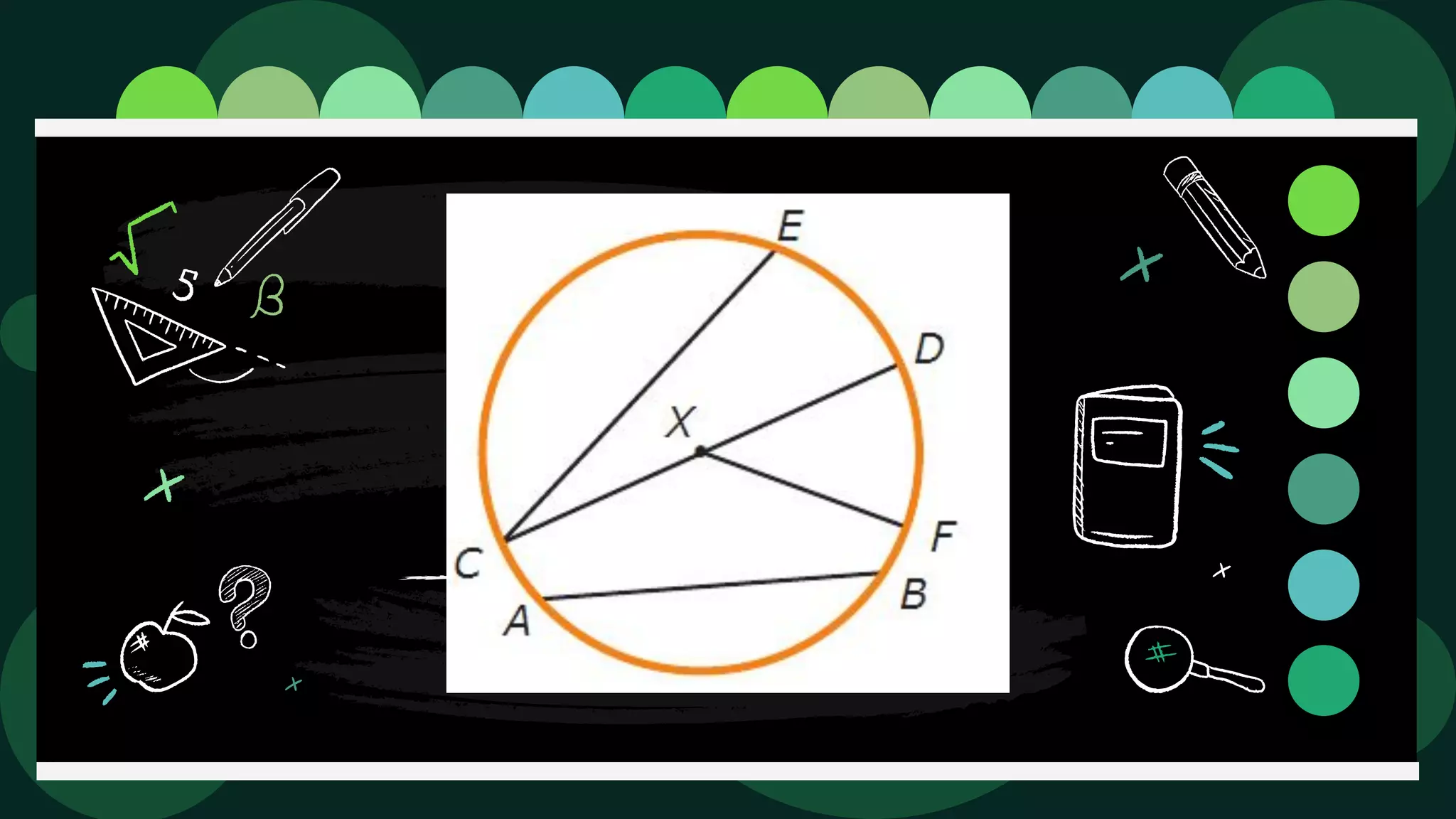
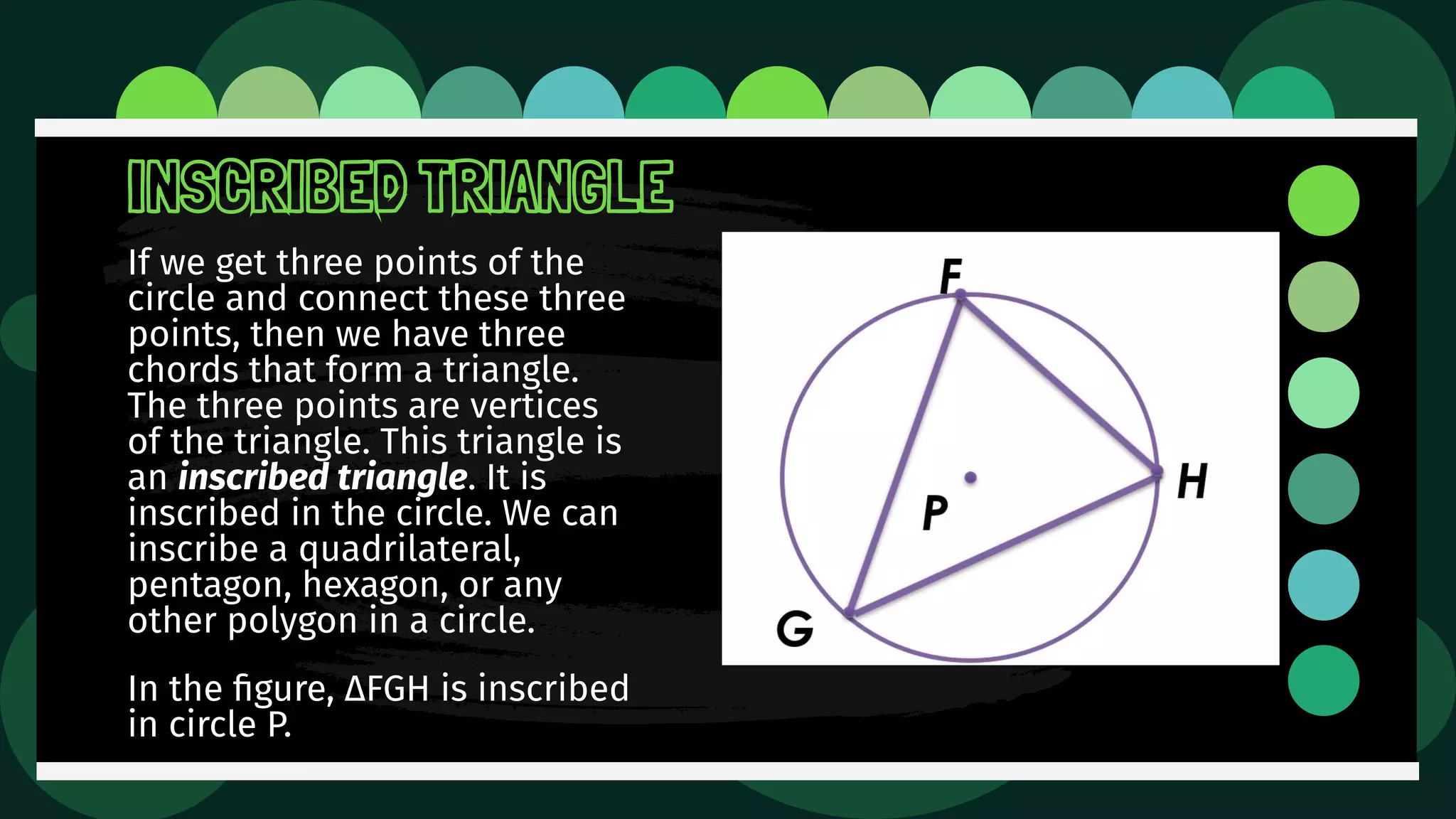
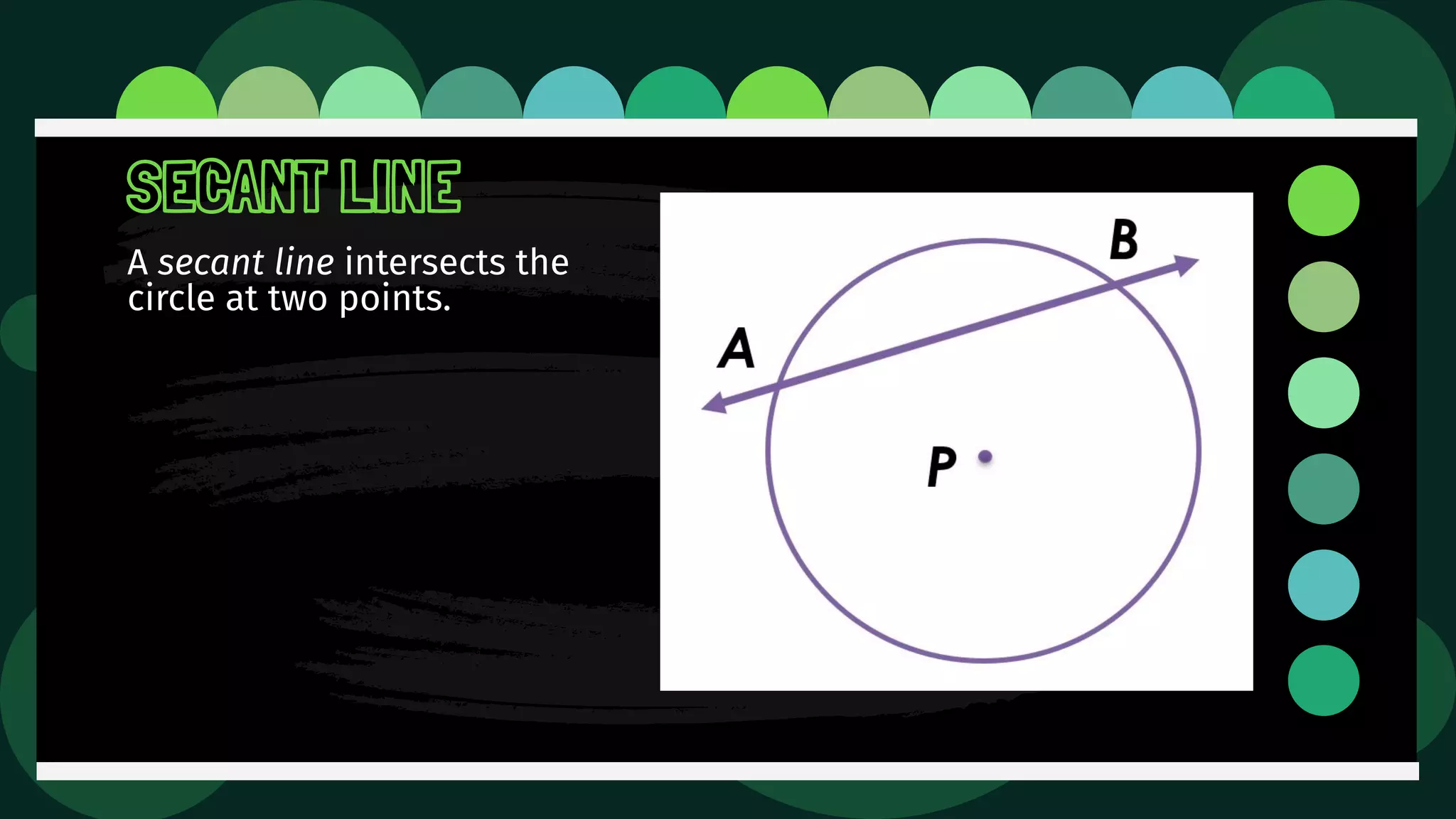
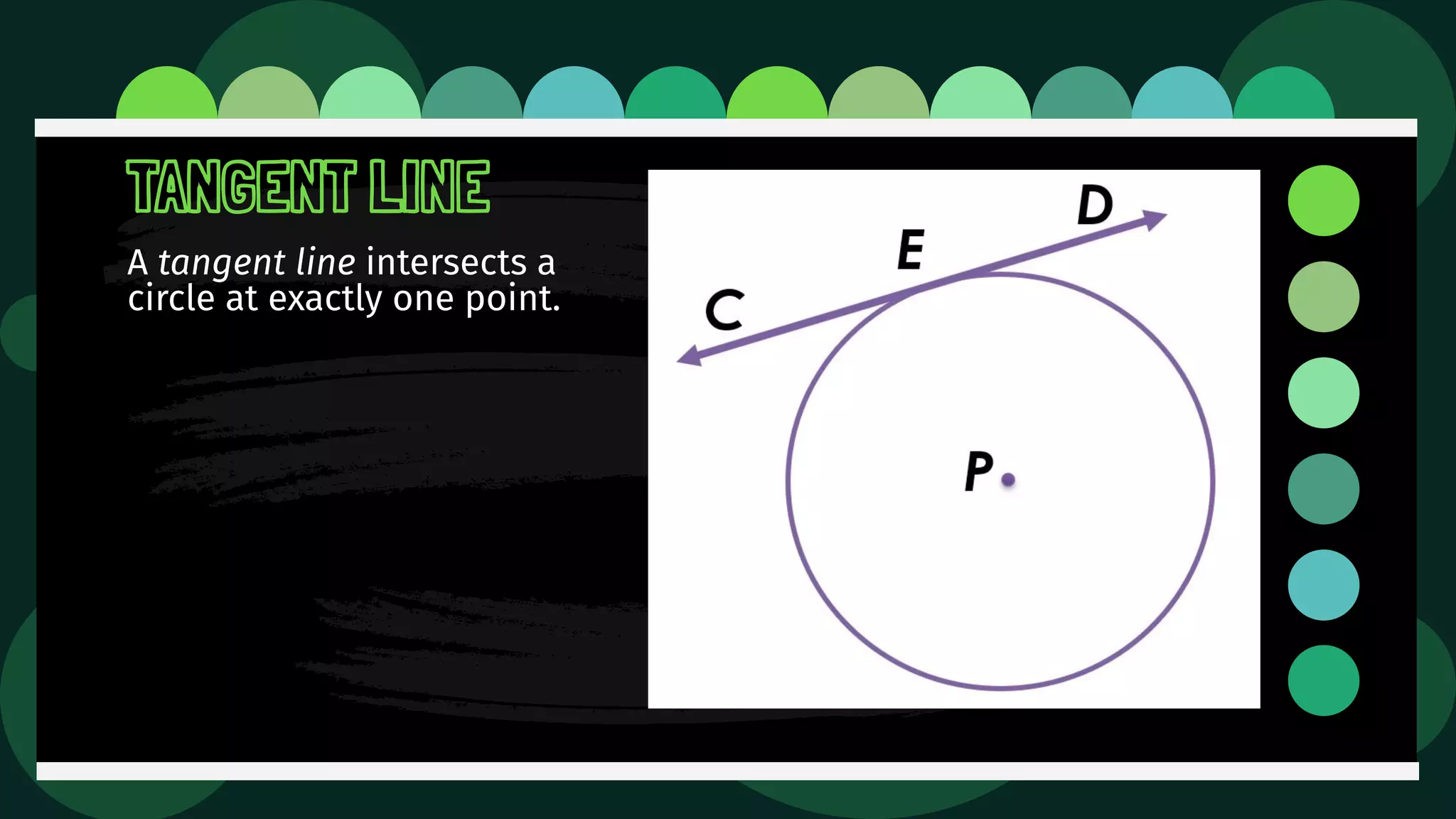
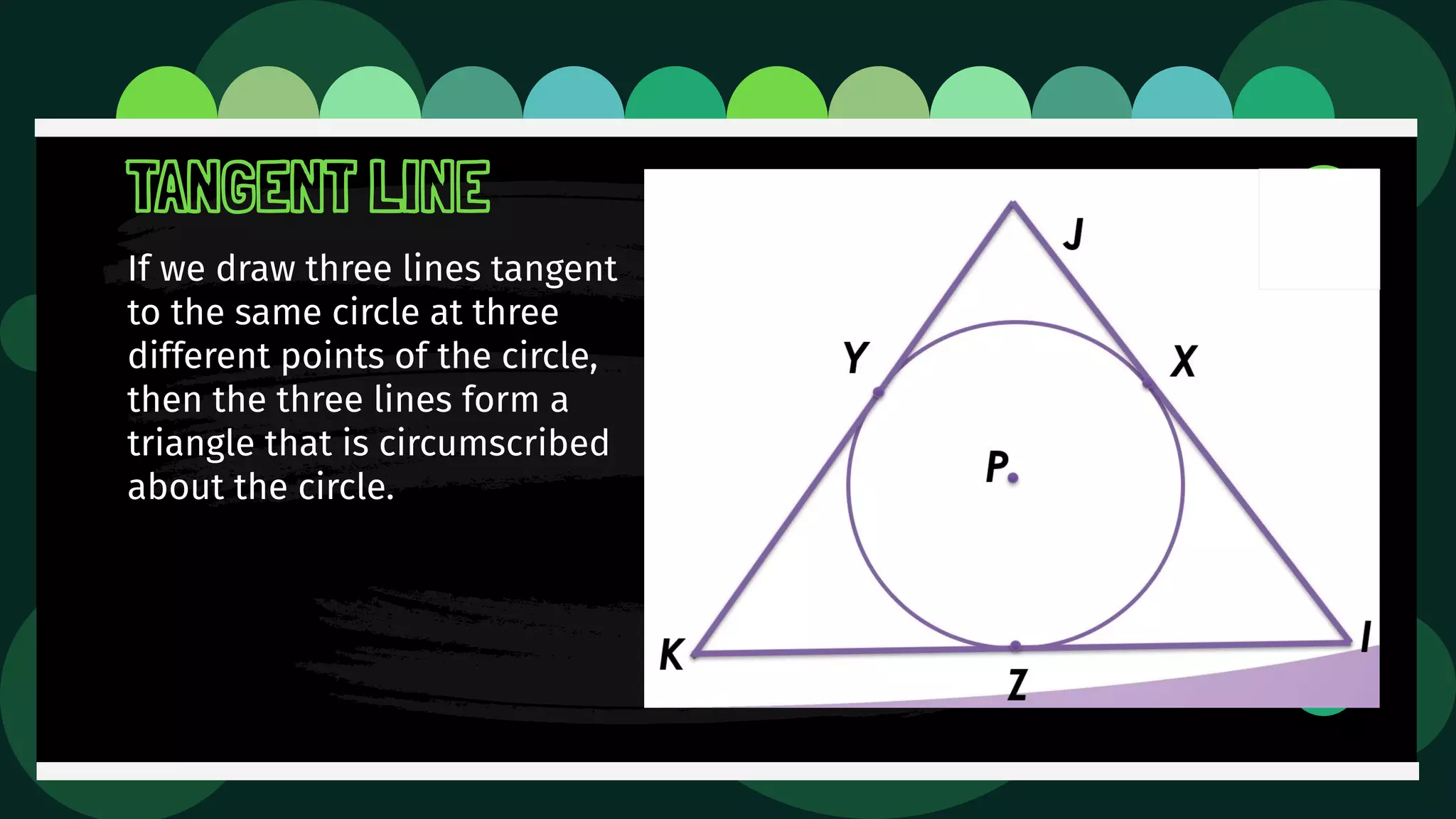
Diane is trying an experiment where she puts a pin through a loop of string and inserts a pencil into the loop. As she stretches the string, she tries to draw a figure. The document then defines and illustrates key terms related to circles such as center, radius, diameter, chord, secant, tangent, inscribed, and circumscribed shapes. It provides examples of each term using diagrams of circles.

1. Diane is trying an experiment.
She put a pin on a board.
Then, she put a loop of string
around it and inserted a pencil
into the loop. She tried to
draw a figure as she stretched
the string.
Can you also try the same
experiment?

2. CIRCLES

3. CIRCLE
● A circle is a set of points
on a flat surface. These
points are equidistant
from a fixed point called
center.

4. CIRCLE
In the figure below, point P is the center of the circle. A circle is
named with its center, using a single letter. The circle below is named
circle P.

5. NAME THE CIRCLES

6. NAME THE CIRCLES

7. NAME THE CIRCLES

8. PARTS OF
CIRCLES

9. The circumference is the
distance around the circle.
CIRCUMFERENCE

10. The radius (r) of a circle is the
segment drawn from the
center to any point on the
circle.
A radius of the circle below is
PM. All radii of a circle are
congruent, since all the points
on a circle are of the same
distance from the center.
RADIUS

11. The diameter (d) of a circle is
the longest segment drawn
across a circle.
The diameter passes through
the center of the circle. The
diameter of the given circle is
MR. The length of the diameter
is twice that of the radius.
Therefore, MP = PR and
MR = MP + PR = d
DIAMETER

12. A chord of a circle is a line
segment that connects any
two points on the circle.
NQ is a chord of circle P. A
chord closer to the center is
longer than a chord farther
from the center. The diameter
of a circle is the longest chord
of the circle.
CHORD

15. If we get three points of the
circle and connect these three
points, then we have three
chords that form a triangle.
The three points are vertices
of the triangle. This triangle is
an inscribed triangle. It is
inscribed in the circle. We can
inscribe a quadrilateral,
pentagon, hexagon, or any
other polygon in a circle.
In the figure, ∆FGH is inscribed
in circle P.
INSCRIBED TRIANGLE

16. A secant line intersects the
circle at two points.
SECANT LINE

17. A tangent line intersects a
circle at exactly one point.
TANGENT LINE

18. If we draw three lines tangent
to the same circle at three
different points of the circle,
then the three lines form a
triangle that is circumscribed
about the circle.
TANGENT LINE