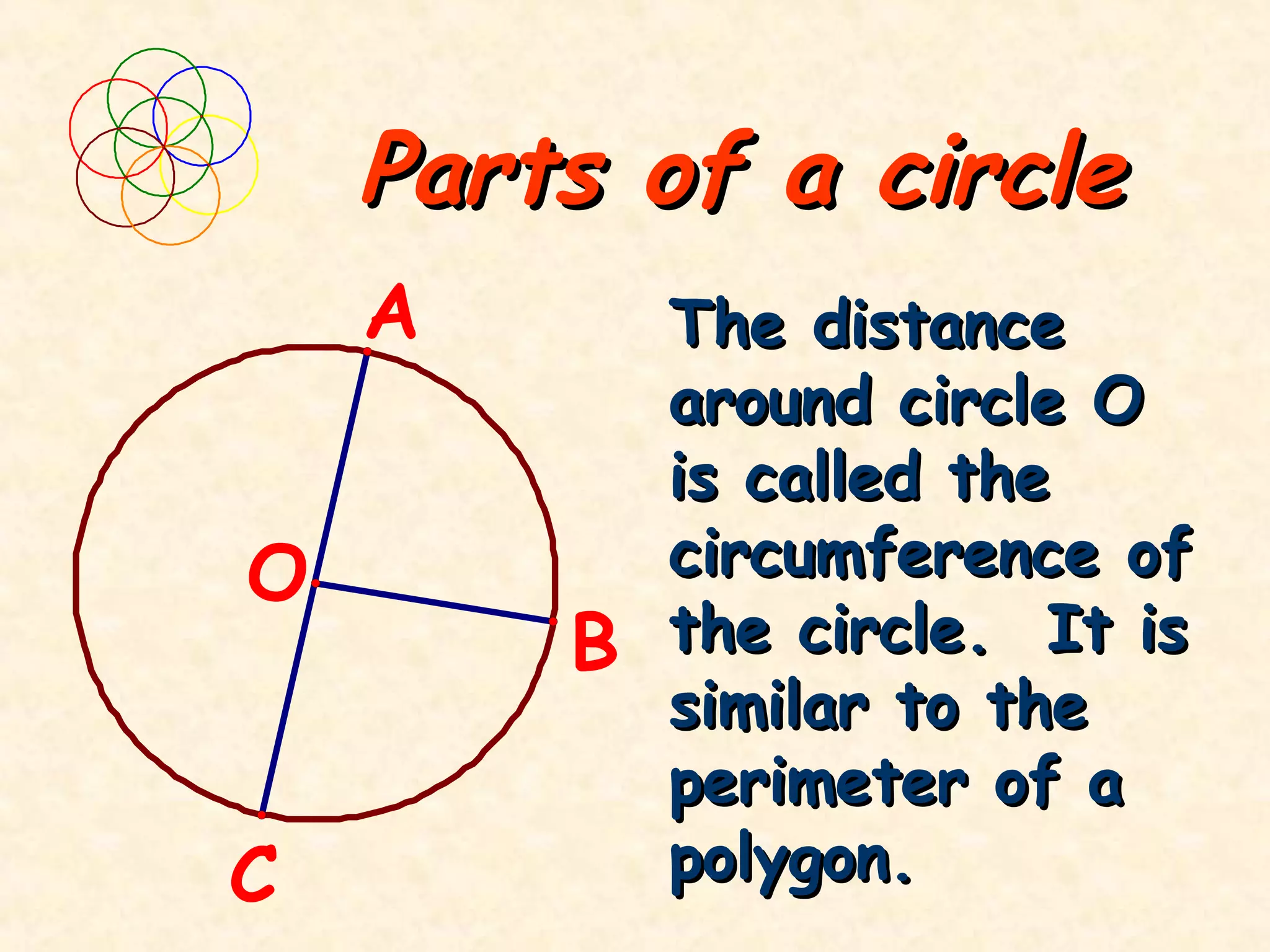
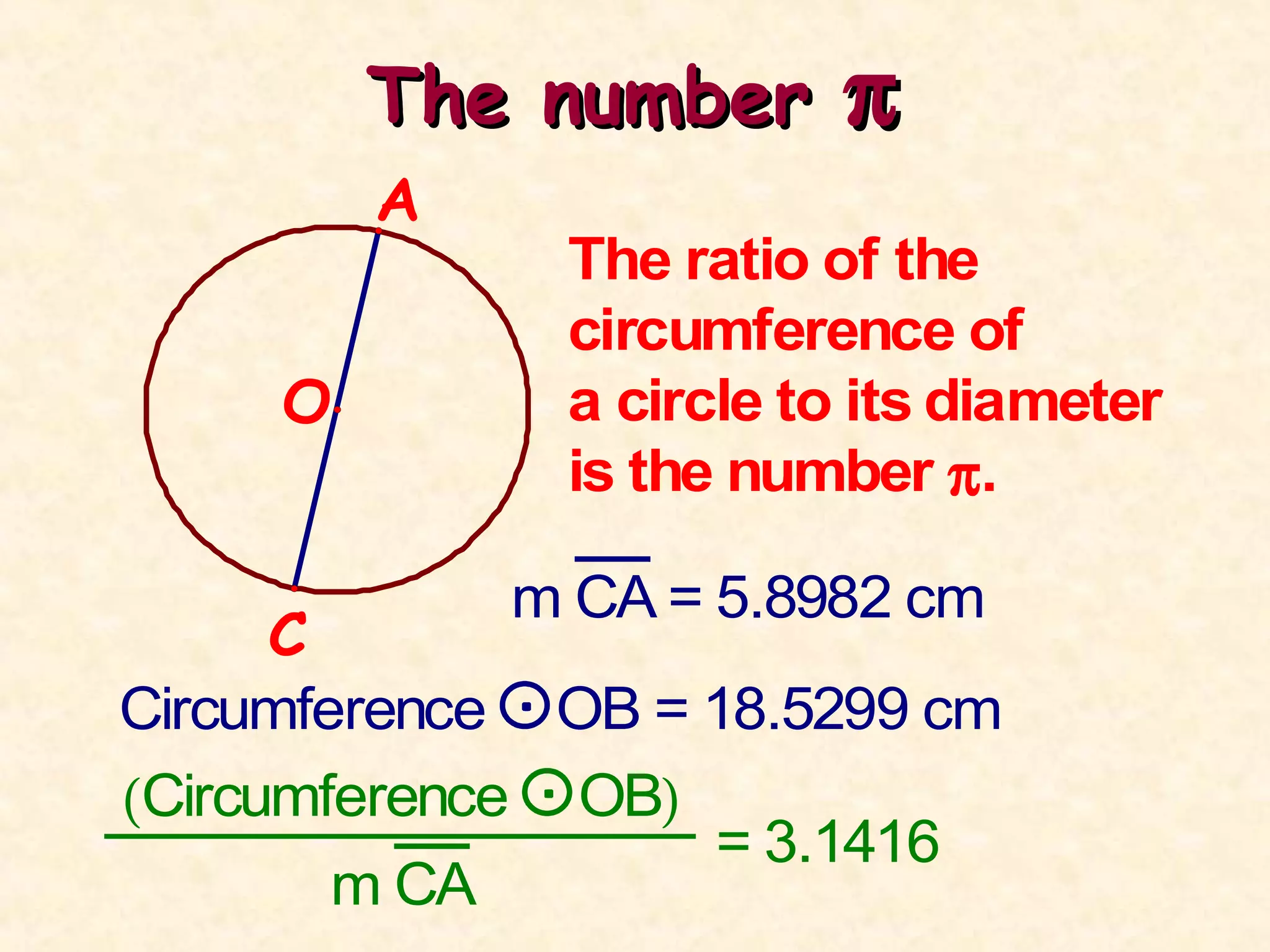
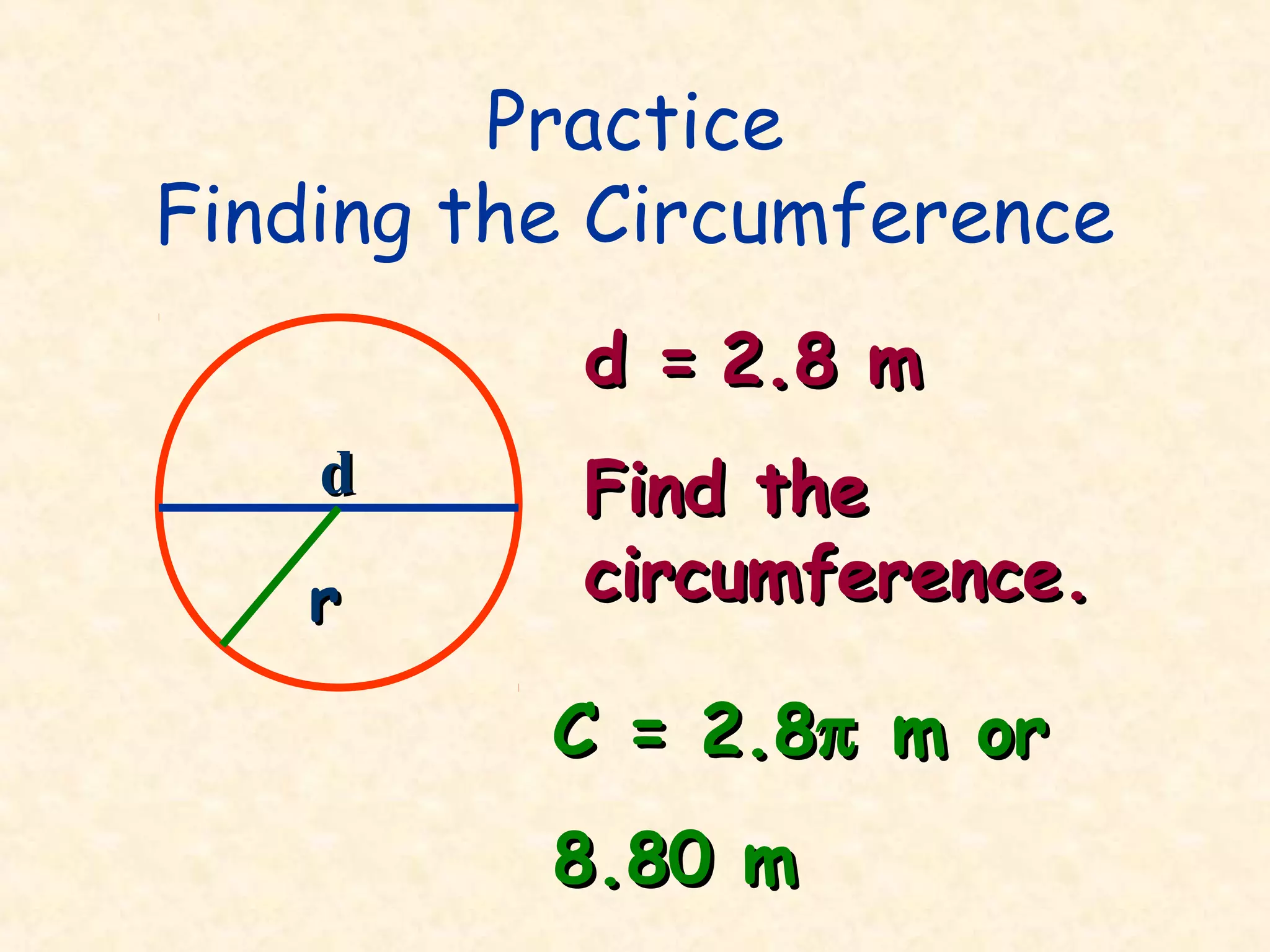
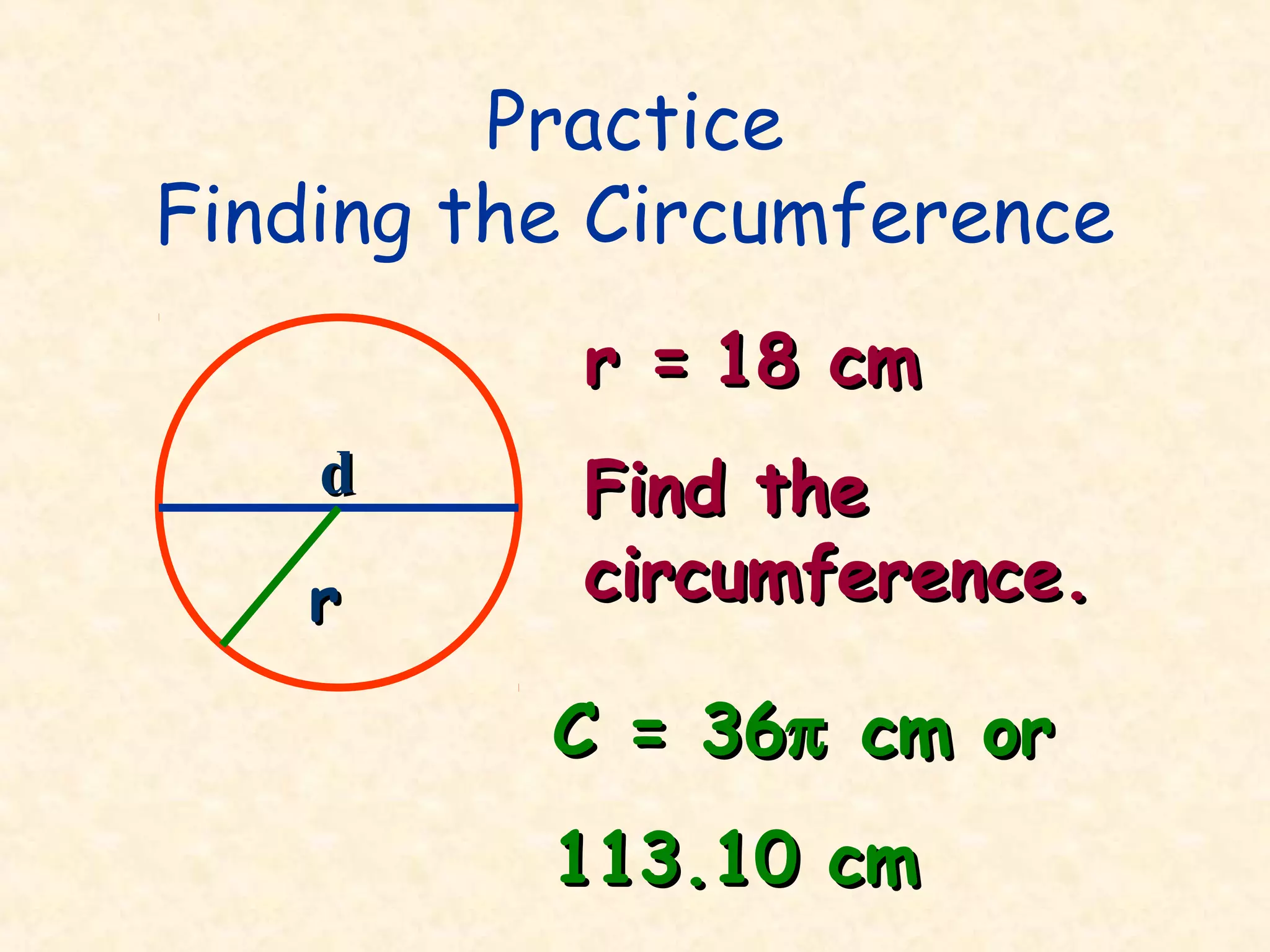
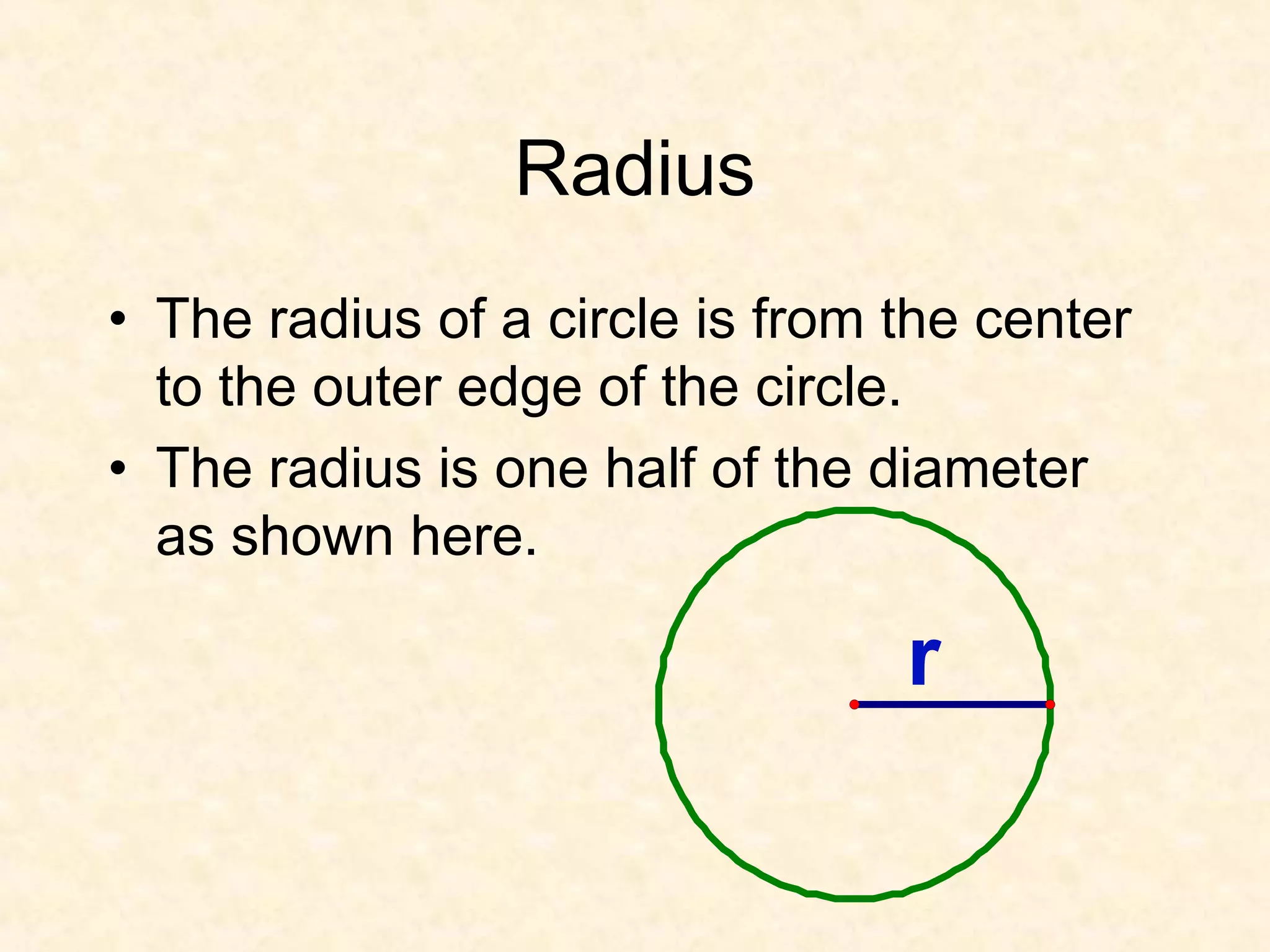
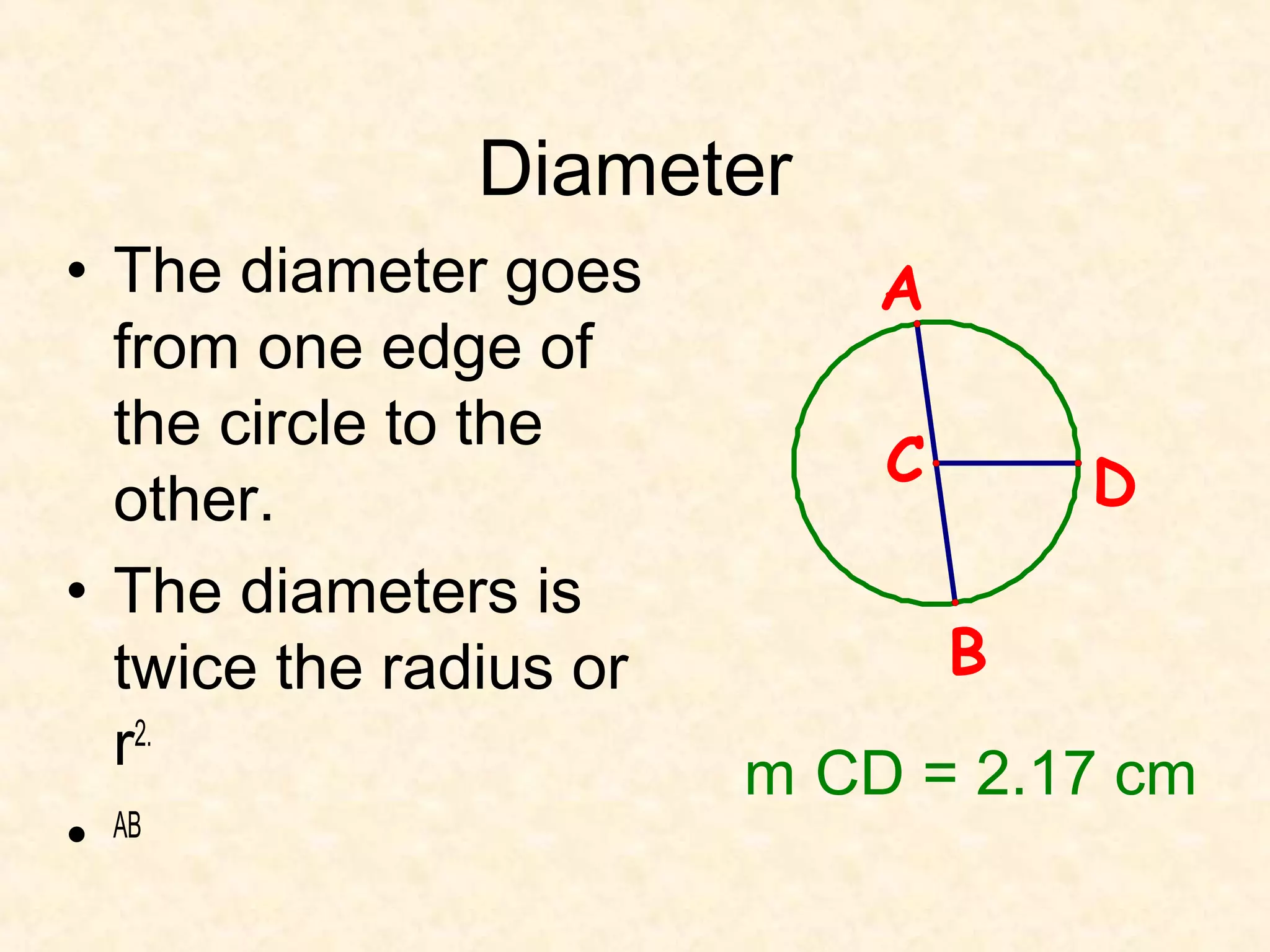
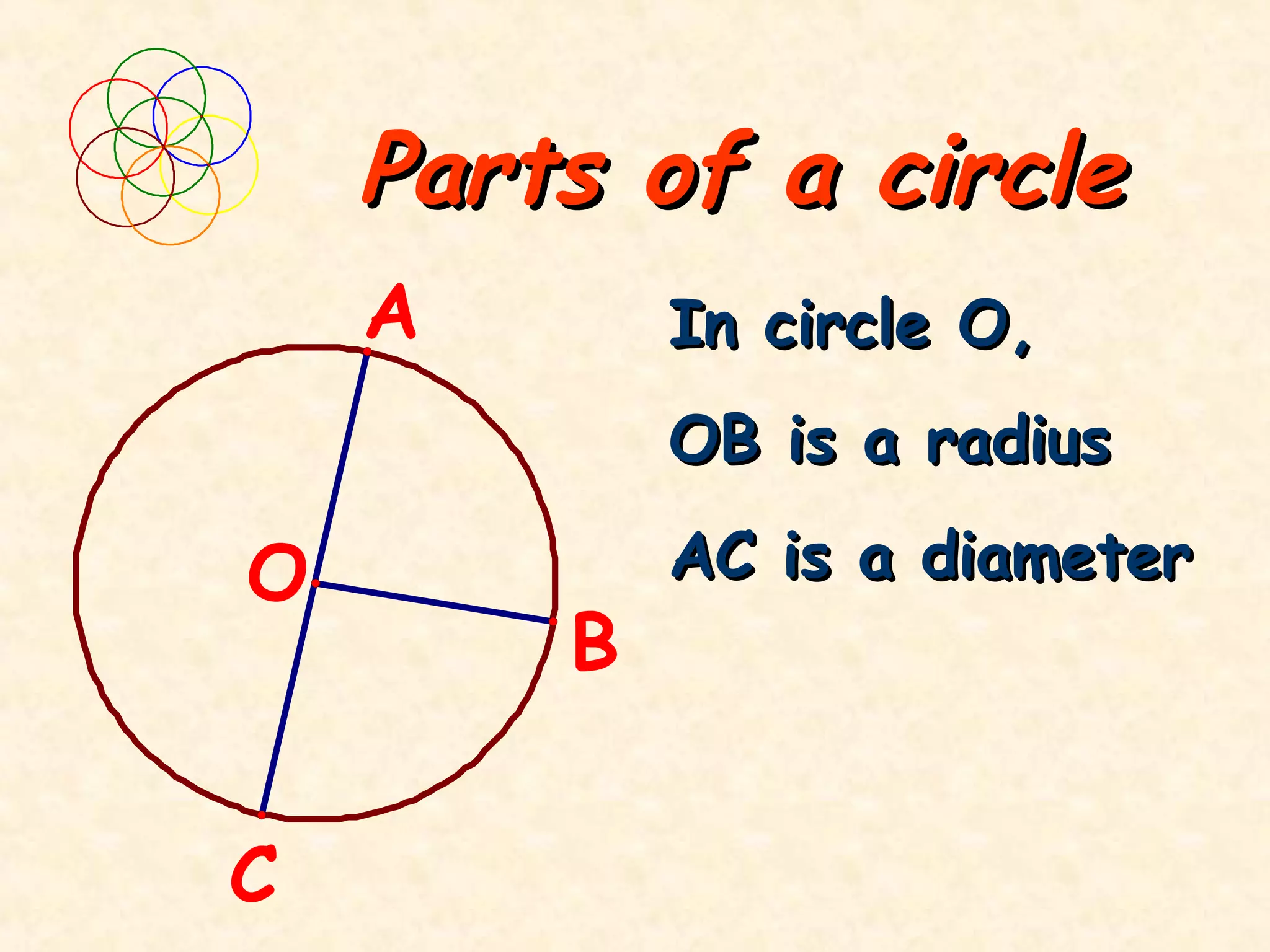
The document discusses key concepts related to circles, including: - The radius of a circle extends from the center to the edge. The diameter spans across the circle. The diameter is twice the radius. - Pi (π) is approximately 3.14 and represents the ratio of a circle's circumference to its diameter. - The circumference is the distance around the circle. It can be calculated as C = 2πr or C = πd. 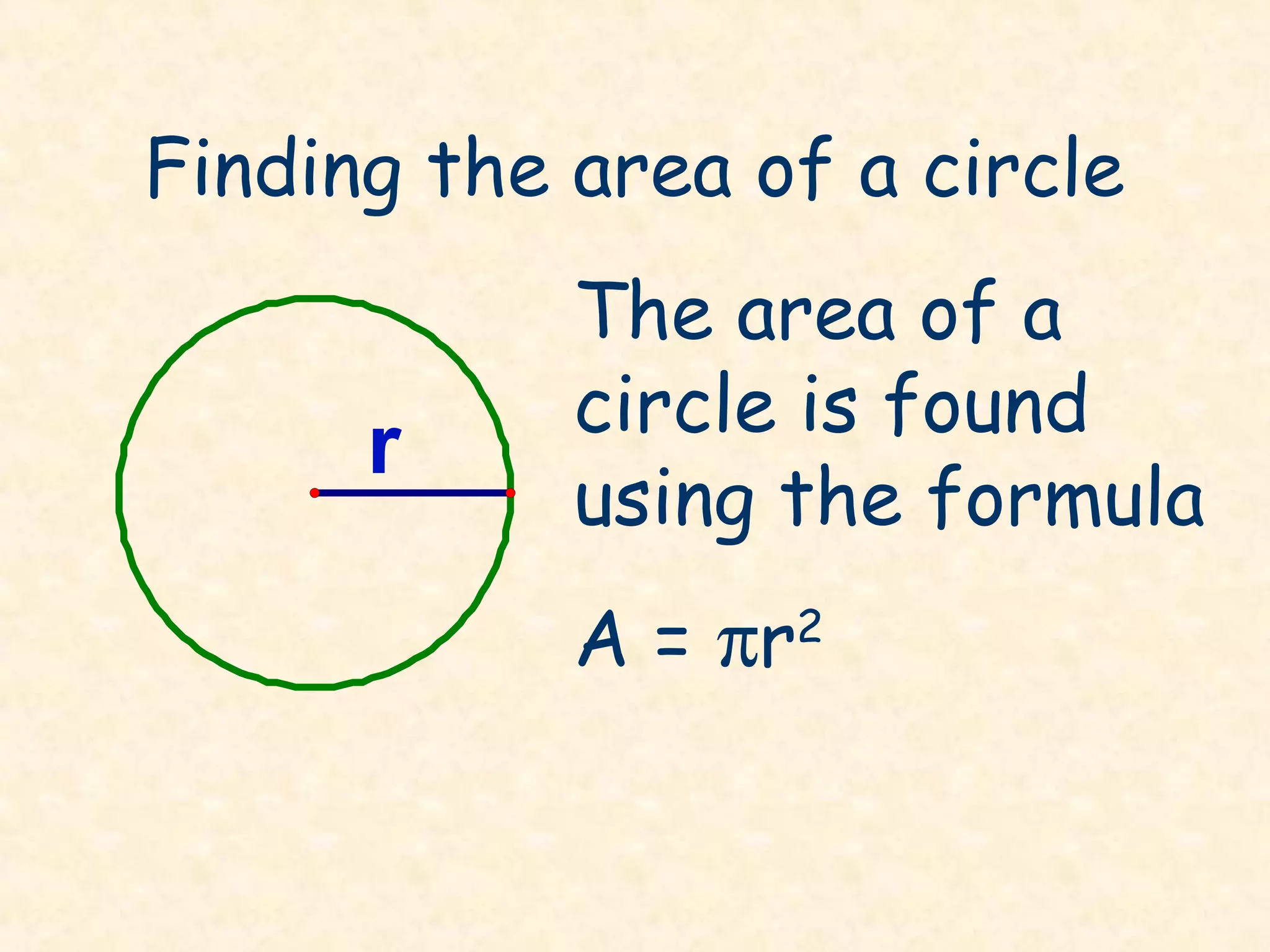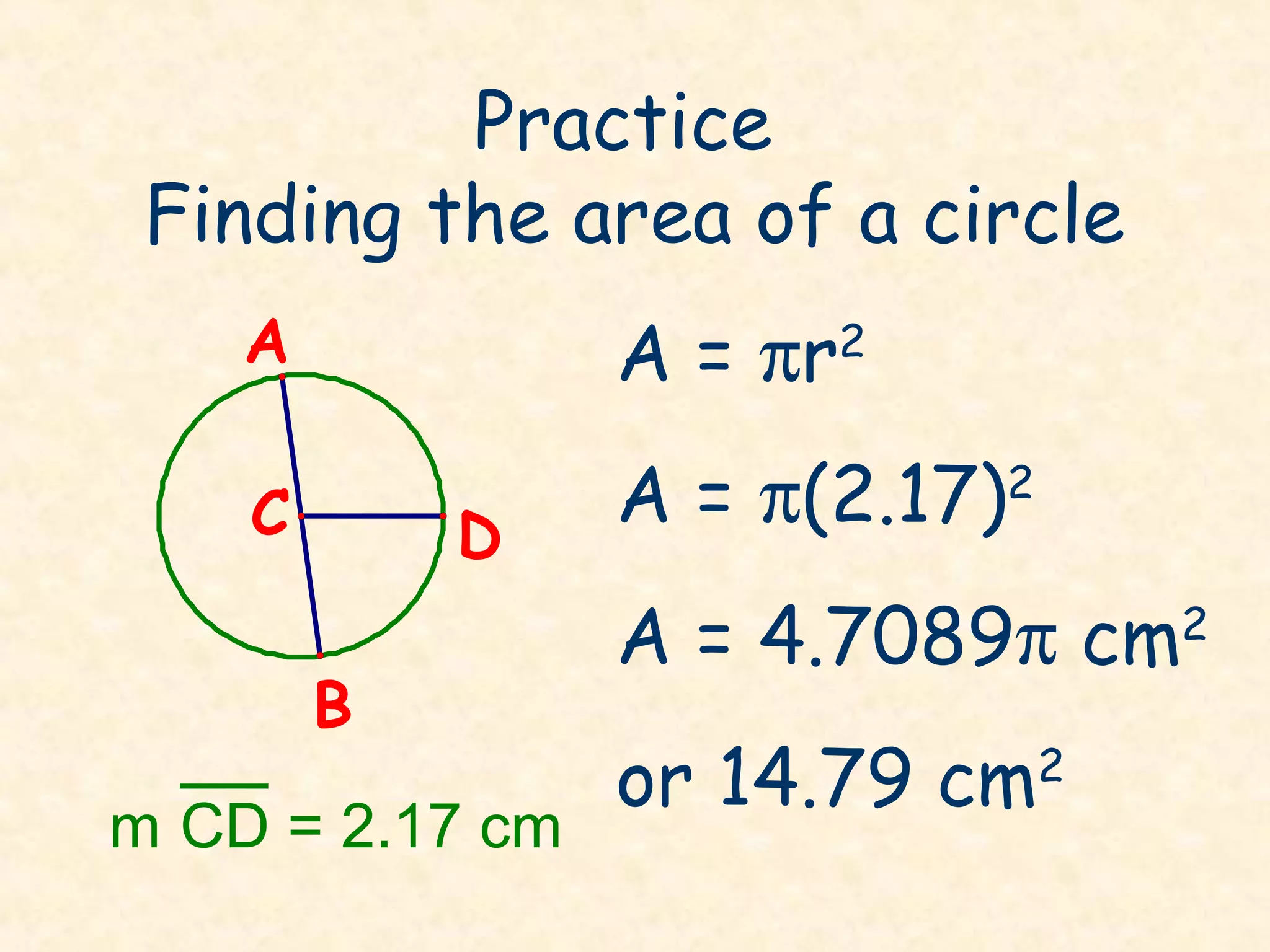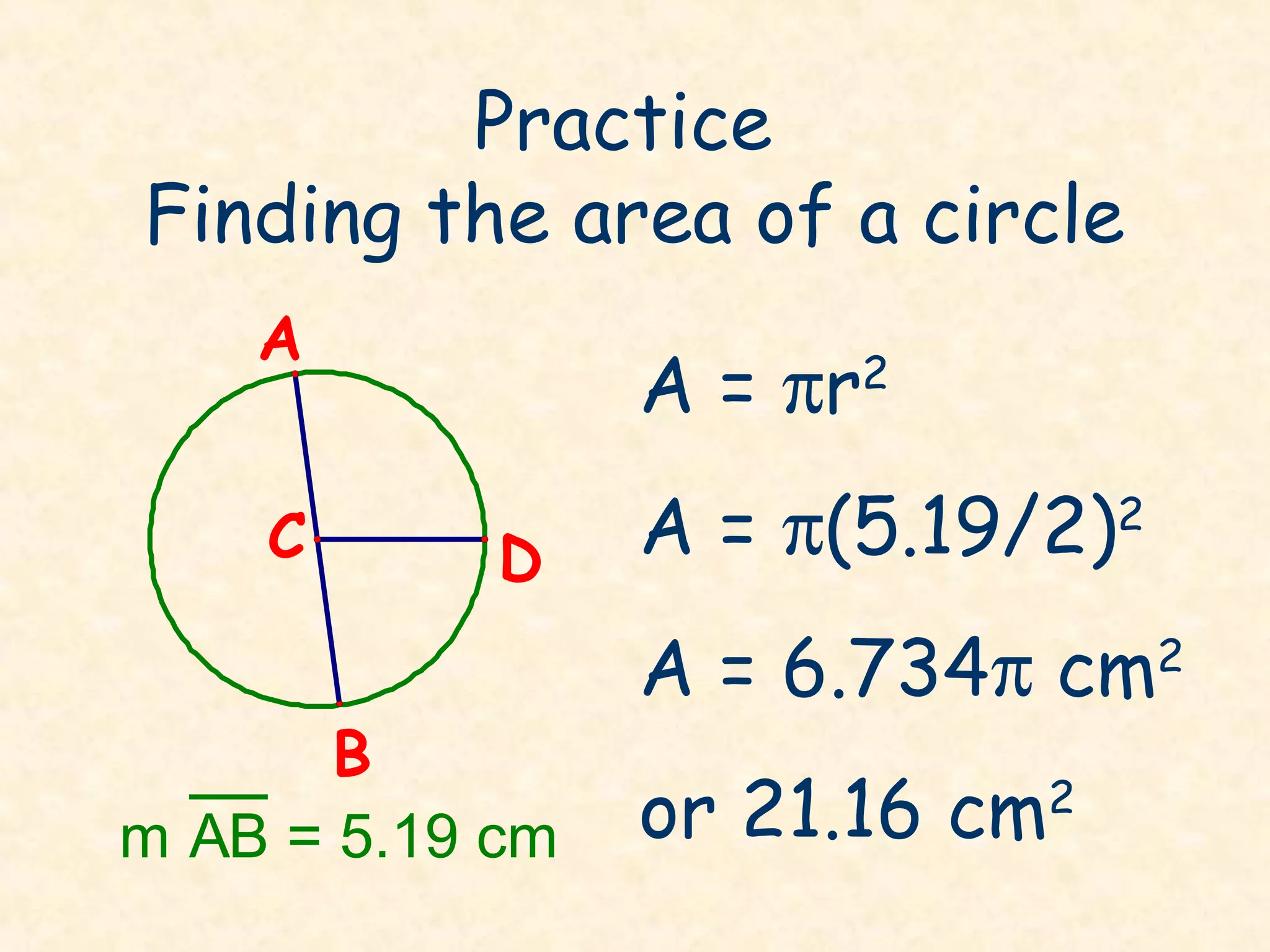- The area of a circle can be found using the formula A = πr^2.

1. Area of
Circles
and Parts
of Circles

2. Radius
• The radius of a circle is from the center
to the outer edge of the circle.
• The radius is one half of the diameter
as shown here.
r

3. Diameter
• The diameter goes A
from one edge of
the circle to the
C D
other.
• The diameters is
twice the radius or B
r2. m CD = 2.17 cm
• AB

4. Pi π
• Pi is ≈ 3.14
• Pi is represented by the symbol
π

5. Parts of a circle
A In circle O,
OB is a radius
O AC is a diameter
B
C

6. Parts of a circle
A The distance
around circle O
is called the
O circumference of
B the circle. It is
similar to the
perimeter of a
C polygon.

7. The number π
A
The ratio of the
circumference of
O a circle to its diameter
is the number π.
m CA = 5.8982 cm
C
Circumference OB = 18.5299 cm
(Circumference OB)
= 3.1416
m CA

8. Finding the Circumference
Since we know
d that C/d = π we
can solve for C.
r
C
(d ) = π(d)
d
Therefore: C = π d or
C = 2π r

9. Practice
Finding the Circumference
d = 46 cm
d Find the
r circumference.
C = 46π cm or
144.51 cm

10. Practice
Finding the Circumference
d = 2.8 m
d Find the
r circumference.
C = 2.8π m or
8.80 m

11. Practice
Finding the Circumference
r = 18 cm
d Find the
r circumference.
C = 36π cm or
113.10 cm

12. Finding the area of a circle
The area of a
circle is found
r
using the formula
A = πr2

13. Practice
Finding the area of a circle
A A = πr2
C D
A = π(2.17)2
A = 4.7089π cm 2
B
or 14.79 cm 2
m CD = 2.17 cm

14. Practice
Finding the area of a circle
A
A = πr2
C D A = π(5.19/2)2
A = 6.734π cm2
B
m AB = 5.19 cm or 21.16 cm2