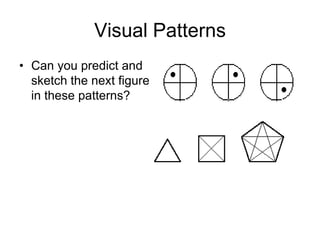
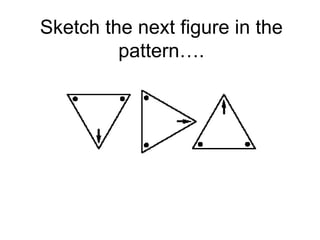
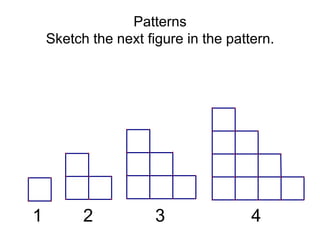
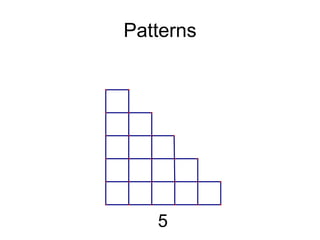
This document discusses inductive reasoning and pattern recognition. It provides examples of how observing patterns in areas like weather, geometry, and numbers can help make predictions. Readers are encouraged to look for patterns, make conjectures based on the patterns, and verify their conjectures to determine if they are true or false, sometimes using counterexamples. The document aims to teach inductive reasoning skills through examples of visual and numeric patterns.

1. 1.1 Patterns and Inductive
Reasoning

2. Inductive Reasoning
• Watching weather patterns
develop help forecasters…
• Predict weather..
• They recognize and…
• Describe patterns.
• They then try to make
accurate predictions based
on the patterns they
discover.

3. Patterns & Inductive Reasoning
• In Geometry, we will
• Study many
patterns…
• Some discovered by
others….
• Some we will
discover…
• And use those
patterns to make
accurate predictions

4. Visual Patterns
• Can you predict and
sketch the next figure
in these patterns?

5. Number Patterns
• Describe a pattern in
the number sequence
and predict the next
number.

6. Using Inductive Reasoning
• Look for a Pattern
• (Looks at several
examples…use pictures
and tables to help
discover a pattern)
• Make a conjecture.
• (A conjecture is an
unproven “guess” based
on observation…it might
be right or
wrong…discuss it with
others…make a new
conjecture if necessary)

7. How do you know your
conjecture is True or False?
• To prove a conjecture is TRUE, you need
to prove it is ALWAYS true (not always
so easy!)
• To prove a conjecture is FALSE, you need
only provide a SINGLE counterexample.
• A counterexample is an example that
shows a conjecture is false.

8. Decide if this conjecture is
TRUE or FALSE.
• All people over 6 feet tall are good basketball
players.
• This conjecture is false (there are plenty of
counterexamples…)
• A full moon occurs every 29 or 30 days.
• This conjecture is true. The moon revolves
around Earth once approximately every 29.5
days.

9. Sketch the next figure in the
pattern….

10. How many squares are in the
next figure?

11. Patterns
Sketch the next figure in the pattern.
1 2 3 4

12. Patterns
5

13. Example
Describe the pattern and predict the next term
• 1, 4, 16, 64, …
The following number is four times the previous number.
(64)(4) = 256
• -5, -2, 4, 13, …
Add 3, then 6, then 9, so the next number would add 12.
13 + 12 = 25

14. Using Inductive Reasoning
1. Look for a Pattern- look at several
examples. Use diagrams and tables to
help find a pattern.
2. Make a Conjecture- (an unproven
statement that is based on
observations)
3. Verify the Conjecture- Use logical
reasoning to verify the conjecture. It
must be true in all cases.

15. Counterexamples
• A counterexample is an example that
shows that a conjecture is false.
• Not all conjectures have been proven true
or false. These conjectures are called
unproven or undecided.