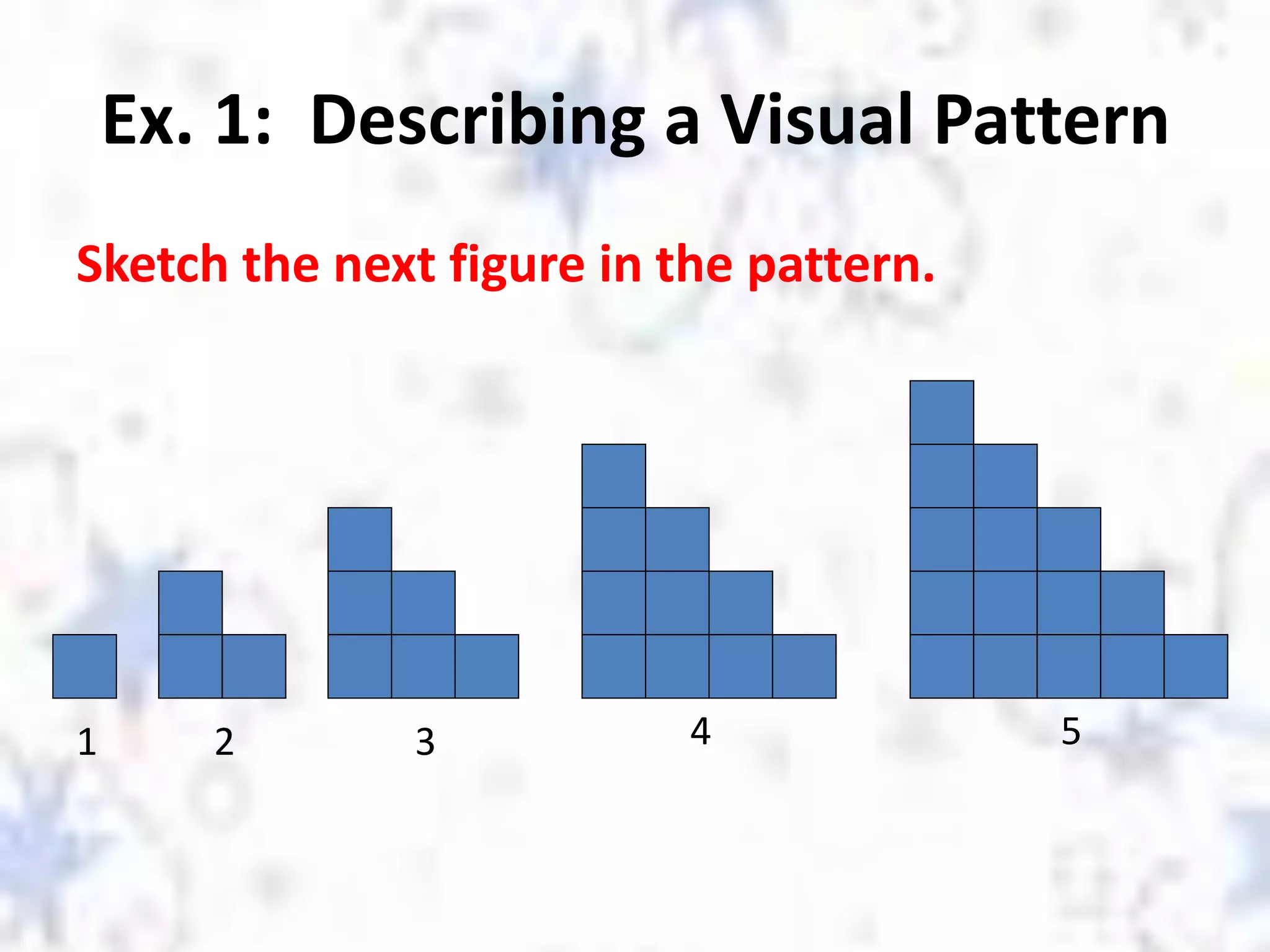
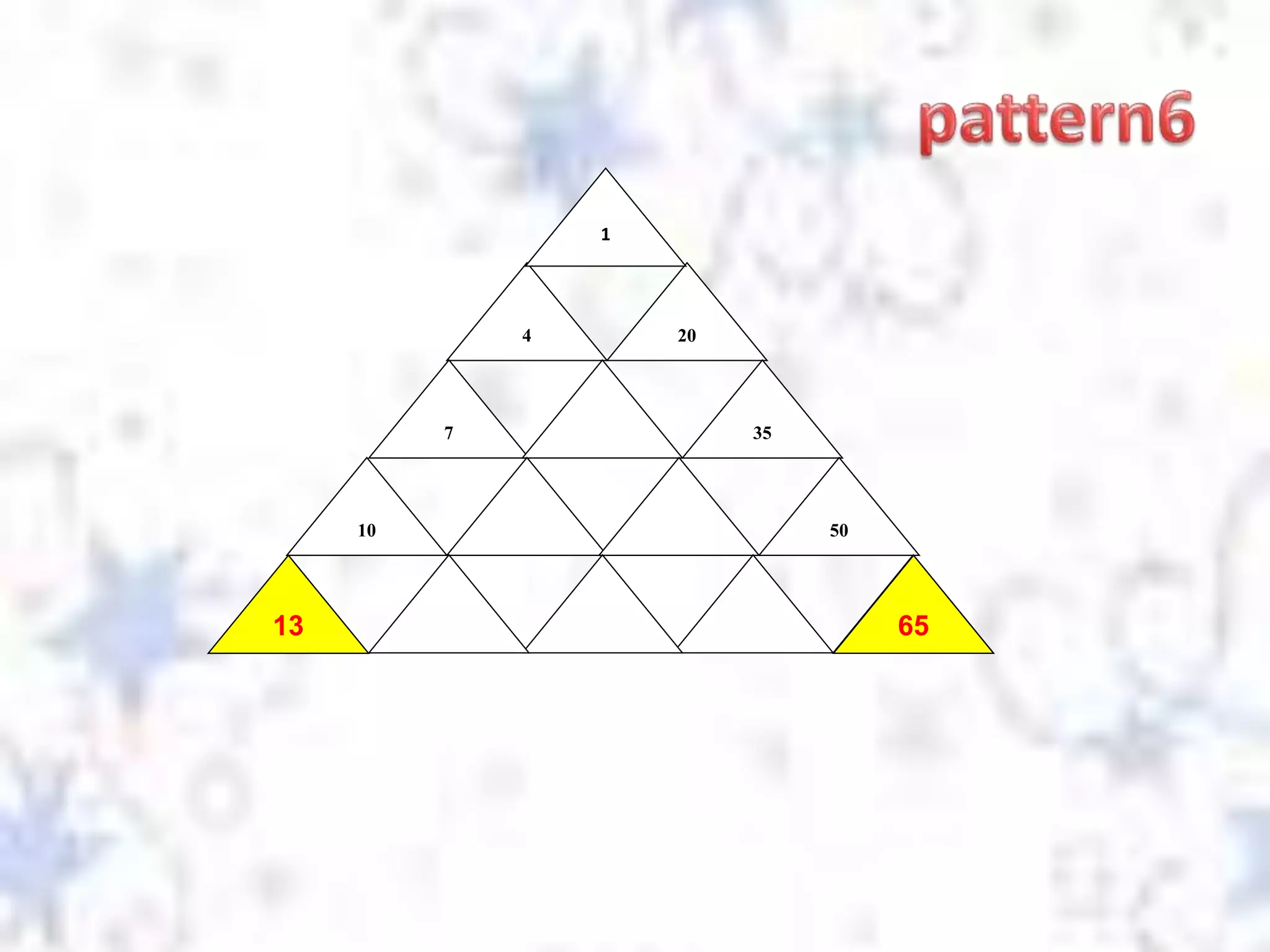
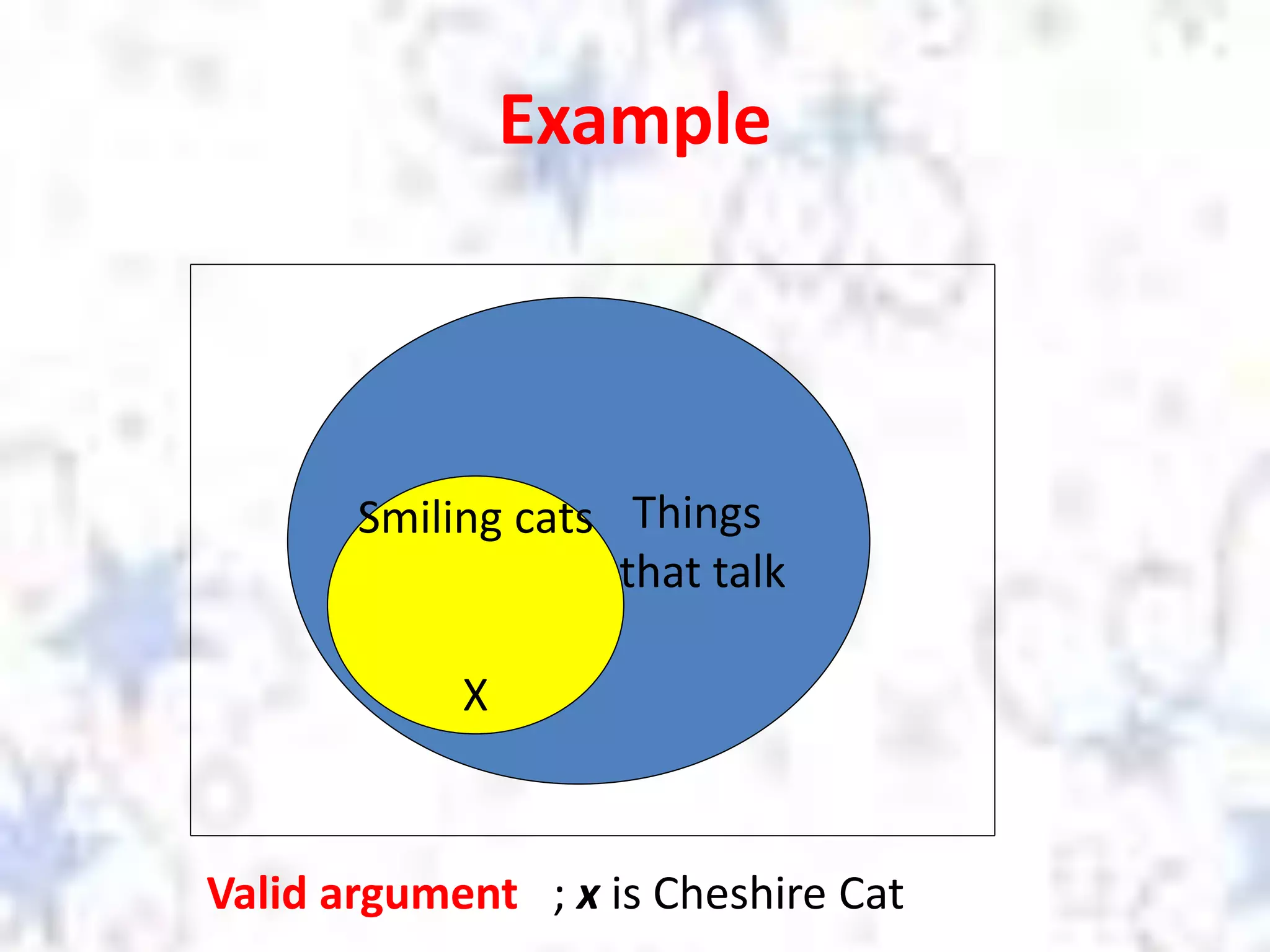
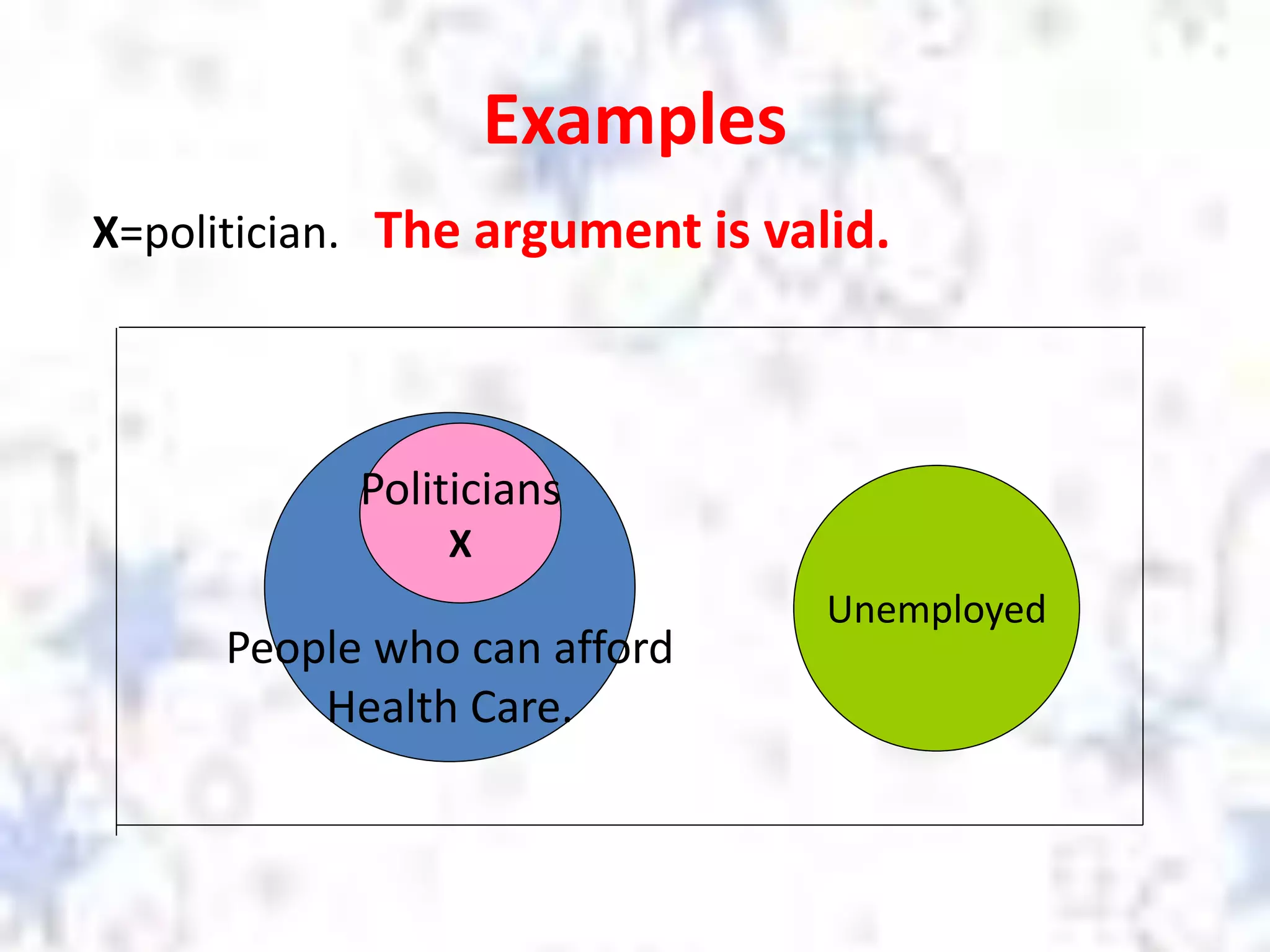
The document discusses different types of reasoning including inductive reasoning and deductive reasoning. It provides examples of each type of reasoning and how they are used. Inductive reasoning involves making generalizations based on specific examples, while deductive reasoning uses general statements to logically prove a specific conclusion. The document explains how to use Venn diagrams to determine if a deductive argument is valid or invalid.

1. Reasoning
by
Nittaya Noinan
Kanchanapisekwittayalai Phetchabun School

2. Reasoning
Human know to use the Reasoning for supporting
faith or for find the truth. The Mathematical Reasoning are
two important ways .
Inductive Reasoning
Deductive Reasoning

3. Inductive Reasoning
Inductive reasoning is the process of
arriving at a general conclusion based
on observations of specific examples.
Example
You purchased textbooks for 4 classes.
Each book cost more than $50.00.
Conclusion: All college textbooks cost
more than $50.00.
Specific General

4. Ex. 1: Describing a Visual Pattern
Sketch the next figure in the pattern.
1 2 3 4 5

5. Ex. 1: Describing a Visual Pattern -
Solution
The sixth figure in the pattern has 6 squares
in the bottom row.
5 6

6. Ex. 2: Describing a Number Pattern
Describe a pattern in
the sequence of
numbers. Predict the
next number.
1
4
16
64
a = ?
How do you get to
the next number?
That’s right.
Each number is 4 times
the previous number.
So, the next number is
a = 256

7. Ex. 3: Describing a Number Pattern
Describe a pattern in
the sequence of
numbers. Predict the
next number.
-5
-2
4
13
b = ?
How do you get to
the next number?
That’s right.
You add 3 to get to the
next number, then 6,
then 9. To find the fifth
number, you add another
multiple of 3 which is +12
or
b = 25

8. Using Inductive Reasoning
Much of the reasoning you need in
geometry consists of 3 stages:
1. Look for a Pattern: Look at several examples.
Use diagrams and tables to help discover
a pattern.
2. Make a Conjecture. Use the example to
make a general conjecture. Okay, what is
that?

9. Using Inductive Reasoning
A conjecture is an unproven statement that
is based on observations. Discuss the
conjecture with others. Modify the
conjecture, if necessary.
3. Verify the conjecture. Use logical reasoning
to verify the conjecture is true IN ALL CASES.

10. Ex. 4: Making a Conjecture
First odd positive integer:
1 = 12
1 + 3 = 4 = 22
1 + 3 + 5 = 9 = 32
1 + 3 + 5 + 7 = 16 = 42
The sum of the first n odd positive integers is n2.

11. 9 x 1 = 9 and 0 + 9 = 9
9 x 2 = 18 and 1 + 8 = 9
9 x 3 = 27 and 2 + 7 = 9
9 x 4 = 36 and 3 + 6 = 9
and
and
and
and
and
and
9 x 5 = 45 4 + 5 = 9
9 x 6 = 54 5 + 4 = 9
9 x 7 = 63 6 + 3 = 9
9 x 8 = 72 7 + 2 = 9
9 x 9 = 81 8 + 1 = 9
9 x 10 = 90 9 + 0 = 9

12. 9 + 1 = 10 and 1 - 1 = 0
9 + 2 = 11 and 2 - 1 = 1
9 + 3 = 12 and 3 - 1 = 2
9 + 4 = 13 and 4 - 1 = 3
and
and
and
and
and
and
9 + 5 = 14 5 - 1 = 4
9 + 6 = 15 6 - 1 = 5
9 + 7 = 16 7 - 1 = 6
9 + 8 = 17 8 - 1 = 7
9 + 9 = 18 9 - 1 = 8
9 + 10 = 19 10 - 1 = 9

13. 3 x 1 = 3
3 x 4 = 12
3 x 7 = 21
3 x 10 = 30
3 x 13 = 39
3 x 16 = 48
3 x 19 = 57
3 x 22 = 66
3 x 25 = 75
3 x 28 = 84
3 x 31 = 93

14. 4 x 2 = 8
14 x 2 = 28
24 x 2 = 48
34 x 2 = 68
44 x 2 = 88
54 x 2 = 108
64 x 2 = 128
74 x 2 = 148
84 x 2 = 168
94 x 2 = 188
104 x 2 = 208

15. 4 20
7 35
10 50
…..…
1
6513

16. Note:
To prove that a conjecture is true, you need to
prove it is true in all cases. To prove that a
conjecture is false, you need to provide a
single counter example. A counterexample is
an example that shows a conjecture is false.

17. Ex. 5: Finding a counterexample
Show the conjecture is false by finding a
counterexample.
Conjecture: For all real numbers x, the
expressions x2 is greater than or equal to x.

18. Ex. 5: Finding a counterexample-
Solution
Conjecture: For all real numbers x, the expressions x2
is greater than or equal to x.
The conjecture is false. Here is a counterexample:
(0.5)2 = 0.25, and 0.25 is NOT greater than or equal
to 0.5. In fact, any number between 0 and 1 is a
counterexample.

19. Note:
Not every conjecture is known to be true or
false. Conjectures that are not known to be
true or false are called unproven or
undecided.

20. Ex. 6: Examining an Unproven
Conjecture
In the early 1700’s, a Prussian mathematician names
Goldbach noticed that many even numbers greater
than 2 can be written as the sum of two primes.
Specific cases:
4 = 2 + 2 10 = 3 + 7 16 = 3 + 13
6 = 3 + 3 12 = 5 + 7 18 = 5 + 13
8 = 3 + 5 14 = 3 + 11 20 = 3 + 17

21. Ex. 6: Examining an Unproven
Conjecture
Conjecture: Every even number greater than 2 can
be written as the sum of two primes.
This is called Goldbach’s Conjecture. No one has
ever proven this conjecture is true or found a
counterexample to show that it is false. As of the
writing of this text, it is unknown if this conjecture is
true or false. It is known; however, that all even
numbers up to 4 x 1014 confirm Goldbach’s
Conjecture.

22. Ex. 7: Using Inductive Reasoning in
Real-Life
Moon cycles. A full moon occurs when the
moon is on the opposite side of Earth from
the sun. During a full moon, the moon
appears as a complete circle.

23. Ex. 7: Using Inductive Reasoning in
Real-Life
• Use inductive reasoning and the information
below to make a conjecture about how often
a full moon occurs.
• Specific cases: In 2005, the first six full moons
occur on January 25, February 24, March 25,
April 24, May 23 and June 22.

24. Ex. 7: Using Inductive Reasoning in Real-
Life - Solution
• A full moon occurs every 29 or 30 days.
• This conjecture is true. The moon revolves around
the Earth approximately every 29.5 days.
• Inductive reasoning is very important to the study of
mathematics. You look for a pattern in specific cases
and then you write a conjecture that you think
describes the general case. Remember, though, that
just because something is true for several specific
cases does not prove that it is true in general.

25. Deductive Reasoning
Deductive reasoning is the process of proving
a specific conclusion from one or more
general statements.
A conclusion that is proved true by deductive
reasoning is called a theorem.
ConclusionPremise
Logical Argument
Calculation
Proof

26. Deductive Reasoning
Example:
The catalog states that all entering
freshmen must take a mathematics
placement test.
Conclusion: You will have to take a
mathematics placement test.
You are an entering freshman.

27. Deductive Reasoning
Example:
If it rains today, I'll carry an umbrella.
Conclusion: I'm not carrying an
umbrella.
It's not raining.

28. Deductive Reasoning
The previous example was wrong
because I never said what I'd do if it
wasn't raining.
– That's what makes deductive reasoning
so difficult; it's easy to get fooled.
– We'll learn more about this when we
study logic.

29. Deductive vs. Inductive Reasoning
The difference between these two types
of reasoning is that
–inductive reasoning tries to generalize
something from some given information,
–deductive reasoning is following a train
of thought that leads to a conclusion.

30. This is called a Venn Diagram for a statement. In the diagram the outside box or
rectangle is used to represent everything. Circles are used to represent general
collections of things. Dots are used to represent specific items in a collection.
There are 3 basic ways that categories of things can fit together.
women
democrats
women democrats
women democrats
All democrats are women. Some democrats are women. No democrats are women.
One circle inside another. Circles overlap. Circles do not touch.
democrats
Laura Bush
women
George
Bush
Laura Bush is a democrat. George Bush is not a woman.
What statement do each of the following Venn Diagrams depict?

31. Putting more than one statement in a diagram. (A previous example)
Hypothesis:
Dr. Daquila voted in the last election.
Only people over 18 years old vote.
Conclusion:
Dr. Daquila is over 18 years old.
Dr.
Daquila
voters
people over 18
IF__THEN__ Statement Construction
Many categorical statements can be made using an if then sentence construction. For example if we
have the statement: All tigers are cats.
cats
tigers
This can be written as an If_then_ statement in
the following way:
If it is a tiger then it is a cat.
This is consistent with how we have been thinking of logical statements. In fact the parts of this
statement even have the same names:
If it is a tiger then it is a cat.
The phrase “it is a tiger” is called the hypothesis. The phrase “it is a cat” is called the conclusion.

32. Can the following statement be deduced?
Hypothesis:
If you are cool then you sit in the back.
If you sit in the back then you can’t see.
Conclusion
If you are cool then you can’t see.
There is only one way this can be drawn! So it can be deduced and the argument is valid!
people who can’t see
people who sit in back
cool people

33. One method that can be used to determine if a statement can be deduced from a collection of
statements that form a hypothesis we draw the Venn Diagram in all possible ways that the hypothesis
would allow. If any of the ways we have drawn is inconsistent with the conclusion the statement can
not be deduced.
Example
Hypothesis:
All football players are talented people.
Pittsburg Steelers are talented people.
Conclusion:
Pittsburg Steelers are football players. (CAN NOT BE DEDUCED and Invalid!)
talented people
football
players
Pittsburg
Steelers
talented people
football players
Pittsburg Steelers
talented people
football
players
Pittsburg
Steelers
Even though one of the ways is consistent with the conclusion there is at least one that is not so this
statement can not be deduced and is not valid.

34. Example
Construct a Venn Diagram to determine the validity of
the given argument.
1. Hypothesis:
All smiling cats talk.
The Cheshire Cat smiles.
Conclusion:
the Cheshire Cat talks.
VALID OR INVALID???

35. Example
Things
that talk
Smiling cats
X
Valid argument ; x is Cheshire Cat

36. Example
Construct a Venn Diagram to determine the validity of
the given argument.
2. Hypothesis:
No one who can afford health insurance is unemployed.
All politicians can afford health insurance.
Conclusion:
no politician is unemployed.
VALID OR INVALID???

37. Examples
People who can afford
Health Care.
Politicians
X
Unemployed
X=politician. The argument is valid.

38. Example
3. Hypothesis:
Some professors wear glasses.
Mr. Einstein wears glasses.
Conclusion:
Mr. Einstein is a professor.
VALID OR INVALID???

39. Example
X
professors glass wearers
X
x is Mr. Einstein. The argument is invalid