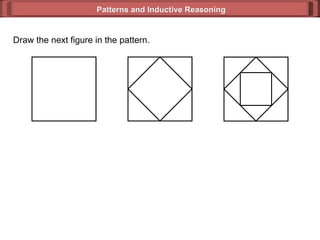
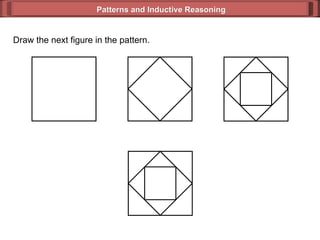
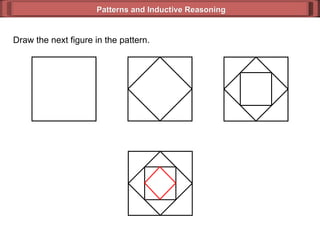
This document discusses inductive reasoning and how it can be used to identify patterns and make predictions. It provides examples of using inductive reasoning to find subsequent terms in numeric sequences and to make conjectures based on patterns observed in geometric figures like rectangles. Key terms discussed include inductive reasoning, conjecture, and counterexample. Readers are guided through activities to practice applying inductive reasoning to sequences and geometric patterns.

1. Patterns and Inductive Reasoning If you were to see dark, towering clouds approaching, you might want to take cover. Your past experience tells you that a thunderstorm is likely to happen. When you make a conclusion based on a pattern of examples or past events, you are using inductive reasoning . You will learn to identify patterns and use inductive reasoning. What You'll Learn

2. Patterns and Inductive Reasoning You can use inductive reasoning to find the next terms in a sequence. Find the next three terms of the sequence: 3, 6, 12,

3. Patterns and Inductive Reasoning You can use inductive reasoning to find the next terms in a sequence. Find the next three terms of the sequence: 3, 6, 12, 24, 48, 96, X 2 X 2 X 2 X 2 X 2

4. Patterns and Inductive Reasoning You can use inductive reasoning to find the next terms in a sequence. Find the next three terms of the sequence: 3, 6, 12, 24, 48, 96, Find the next three terms of the sequence: 7, 8, 11, X 2 X 2 X 2 X 2 X 2

5. Patterns and Inductive Reasoning You can use inductive reasoning to find the next terms in a sequence. Find the next three terms of the sequence: 3, 6, 12, 24, 48, 96, Find the next three terms of the sequence: 7, 8, 11, 16, 32 23, X 2 X 2 X 2 X 2 X 2 + 3 + 1 + 5 + 7 + 9

6. Patterns and Inductive Reasoning Draw the next figure in the pattern.

7. Patterns and Inductive Reasoning Draw the next figure in the pattern.

8. Patterns and Inductive Reasoning Draw the next figure in the pattern.

9. Patterns and Inductive Reasoning A _________ is a conclusion that you reach based on inductive reasoning. In the following activity, you will make a conjecture about rectangles. conjecture 1) Draw several rectangles on your grid paper. 2) Draw the diagonals by connecting each corner with its opposite corner. Then measure the diagonals of each rectangle. 3) Record your data in a table d 1 = 7.5 in. d 2 = 7.5 in. 7.5 inches 7.5 inches Rectangle 1 Diagonal 2 Diagonal 1

10. Patterns and Inductive Reasoning A _________ is a conclusion that you reach based on inductive reasoning. In the following activity, you will make a conjecture about rectangles. conjecture 1) Draw several rectangles on your grid paper. 2) Draw the diagonals by connecting each corner with its opposite corner. Then measure the diagonals of each rectangle. 3) Record your data in a table Make a conjecture about the diagonals of a rectangle d 1 = 7.5 in. d 2 = 7.5 in. 7.5 inches 7.5 inches Rectangle 1 Diagonal 2 Diagonal 1

11. Patterns and Inductive Reasoning A conjecture is an educated guess. Sometimes it may be true, and other times it may be false. How do you know whether a conjecture is true or false? Try different examples to test the conjecture. If you find one example that does not follow the conjecture, then the conjecture is false. Such a false example is called a _____________. counterexample Conjecture: The sum of two numbers is always greater than either number. Is the conjecture TRUE or FALSE ?

12. Patterns and Inductive Reasoning A conjecture is an educated guess. Sometimes it may be true, and other times it may be false. How do you know whether a conjecture is true or false? Try different examples to test the conjecture. If you find one example that does not follow the conjecture, then the conjecture is false. Such a false example is called a _____________. counterexample Conjecture: The sum of two numbers is always greater than either number. Is the conjecture TRUE or FALSE ? Counterexample: -5 + 3 = - 2 - 2 is not greater than 3.

13. Patterns and Inductive Reasoning End of Lesson