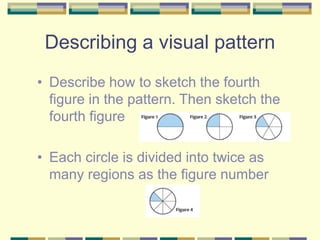
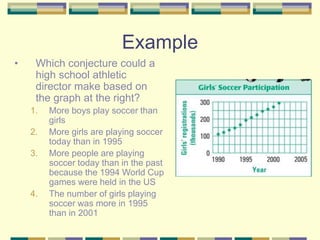
This document discusses inductive reasoning and making conjectures based on patterns. It provides examples of describing number and visual patterns to make conjectures, such as conjecturing that the sum of any three consecutive integers is three times the middle number. The document also discusses using counterexamples to disprove conjectures, such as finding a case where the sum of two numbers is not greater than the larger number. The goal is to understand inductive reasoning and how to formulate and test conjectures.

1. Chapter 2
Reasoning and Proof
Lesson 2.1
Use Inductive Reasoning

2. What will you learn?
• To describe patters and use inductive
reasoning, so you can make predictions
• CA Standard 1
• Students demonstrate understanding by
identifying and giving examples of inductive
reasoning
• CA Standard 3
• Students give counterexamples to disprove
a statement

3. Describing a visual pattern
• Describe how to sketch the fourth
figure in the pattern. Then sketch the
fourth figure
• Each circle is divided into twice as
many regions as the figure number

4. Describing a number pattern
• Describe a pattern in the numbers
-7, -21, -63, -189, … and write the next
three numbers in the pattern
• Each number is 3 times the previous
number
• The next three numbers are -567,
-1701, and -5103

5. Conjecture
• An unproven statement that is based
on observations

6. Inductive Reasoning
• When you find a pattern in specific
cases and then write a conjecture for
the general case

7. Example
• Given five collinear points, make a conjecture
about the number of ways to connect different
pairs of the points.
• Conjecture: You can connect five collinear
points 6 + 4 or 10 different ways

8. Example
• Numbers such as 3, 4 and 5 are called consecutive
integers. Make and test a conjecture about the sum
of any three consecutive integers
• Find a pattern using small groups of numbers
• 3 + 4 + 5 = 12 = 4 ● 3
• 7 + 8 + 9 = 24 = 8 ● 3
• 10 + 11 + 12 = 33 = 11 ● 3
• Conjecture: The sum of any three consecutive
integers is three times the second number
• Test your conjecture
• -1 + 0 + 1 = 0 = 0 ● 3 √
• 100 + 101 + 102 = 303 = 101 ● 3 √

9. Counterexample
• A specific case for which the
conjecture is false

10. Disproving conjectures
• To show that a conjecture is true, you
must show that it is true for all cases
• You can show that a conjecture is false
by simply finding one counterexample

11. Example
• Conjecture: The sum of two
numbers is always greater than
the larger number
• Find a counterexample to
disprove the student’s conjecture
• -2 + -3 = -5
• -5 > -2

12. Example
• Which conjecture could a
high school athletic
director make based on
the graph at the right?
1. More boys play soccer than
girls
2. More girls are playing soccer
today than in 1995
3. More people are playing
soccer today than in the past
because the 1994 World Cup
games were held in the US
4. The number of girls playing
soccer was more in 1995
than in 2001

13. You now know,
• What is a conjecture
• Unproven statement based on observations
• What is inductive reasoning
• Reasoning in which you find patterns and make
conjectures
• What is a counterexample
• A specific case that proves a conjecture false