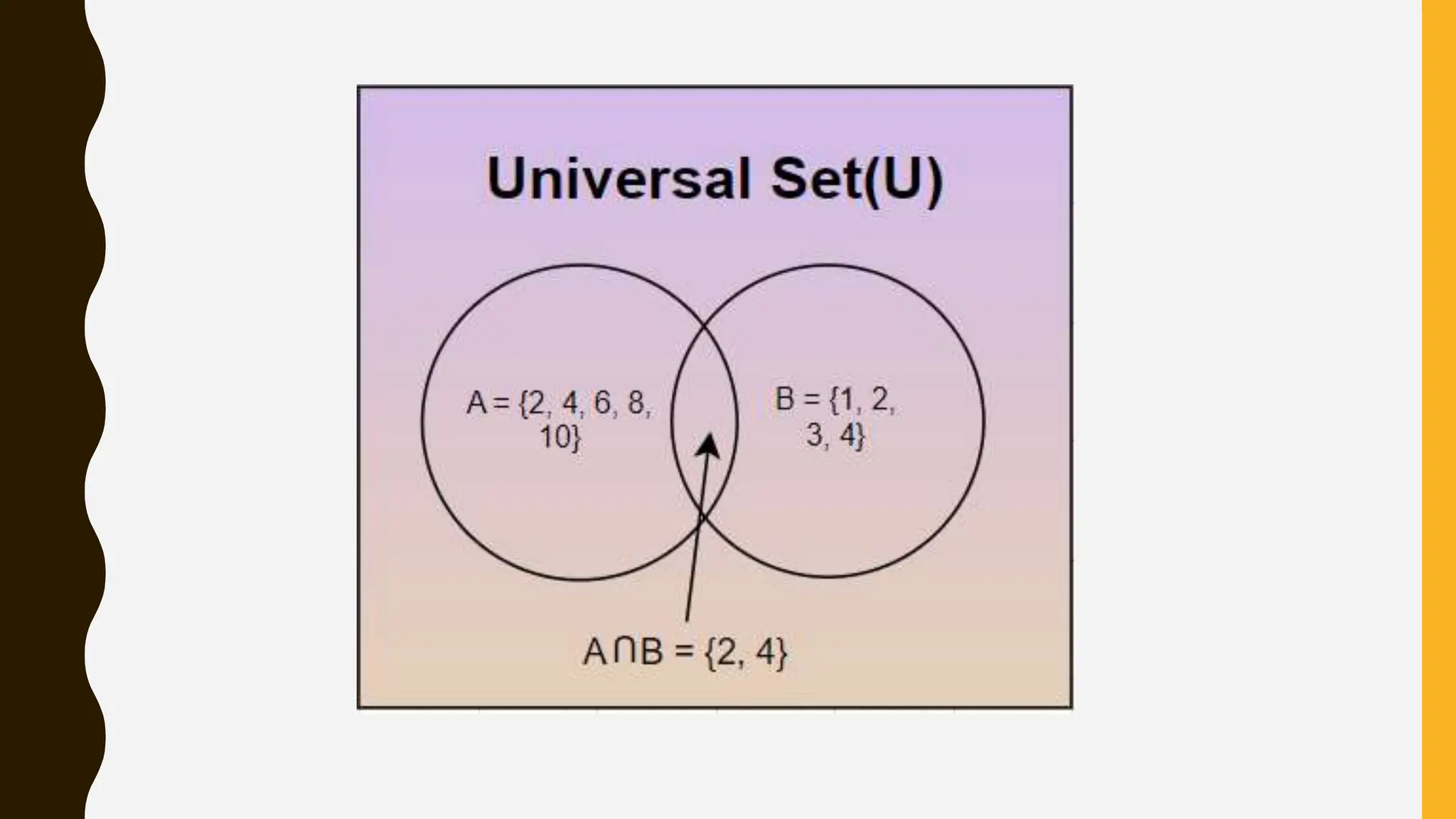
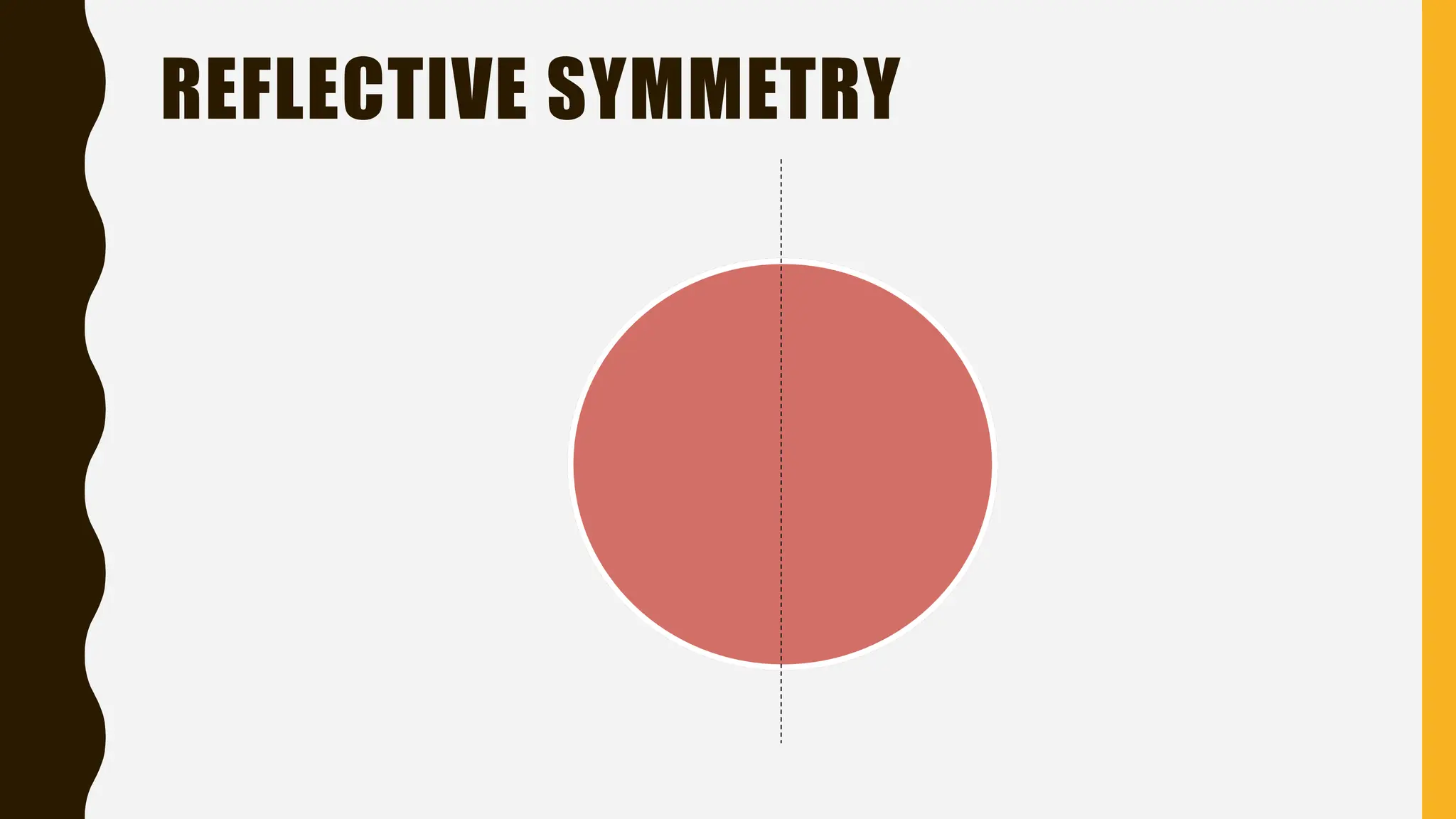
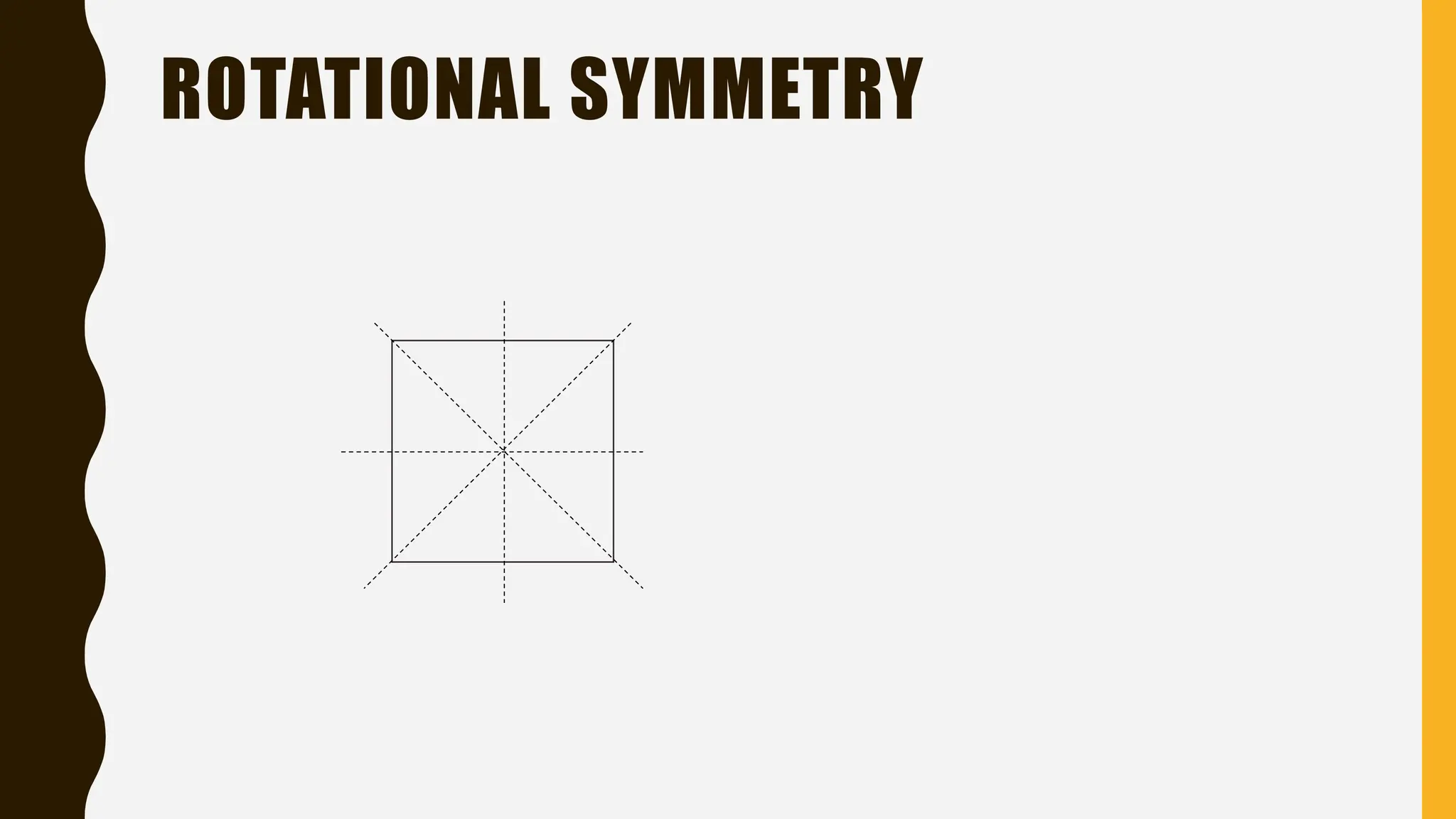
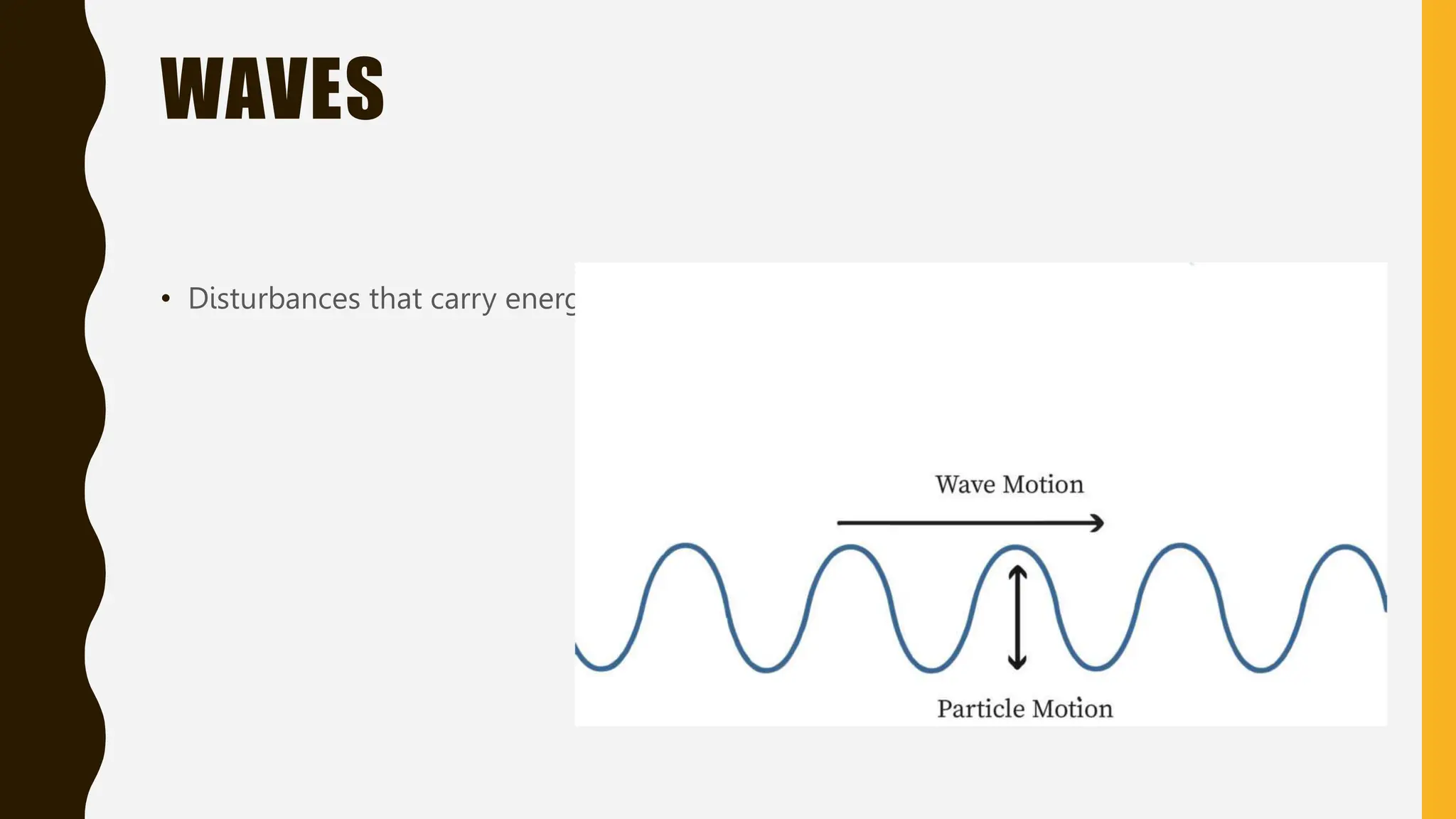
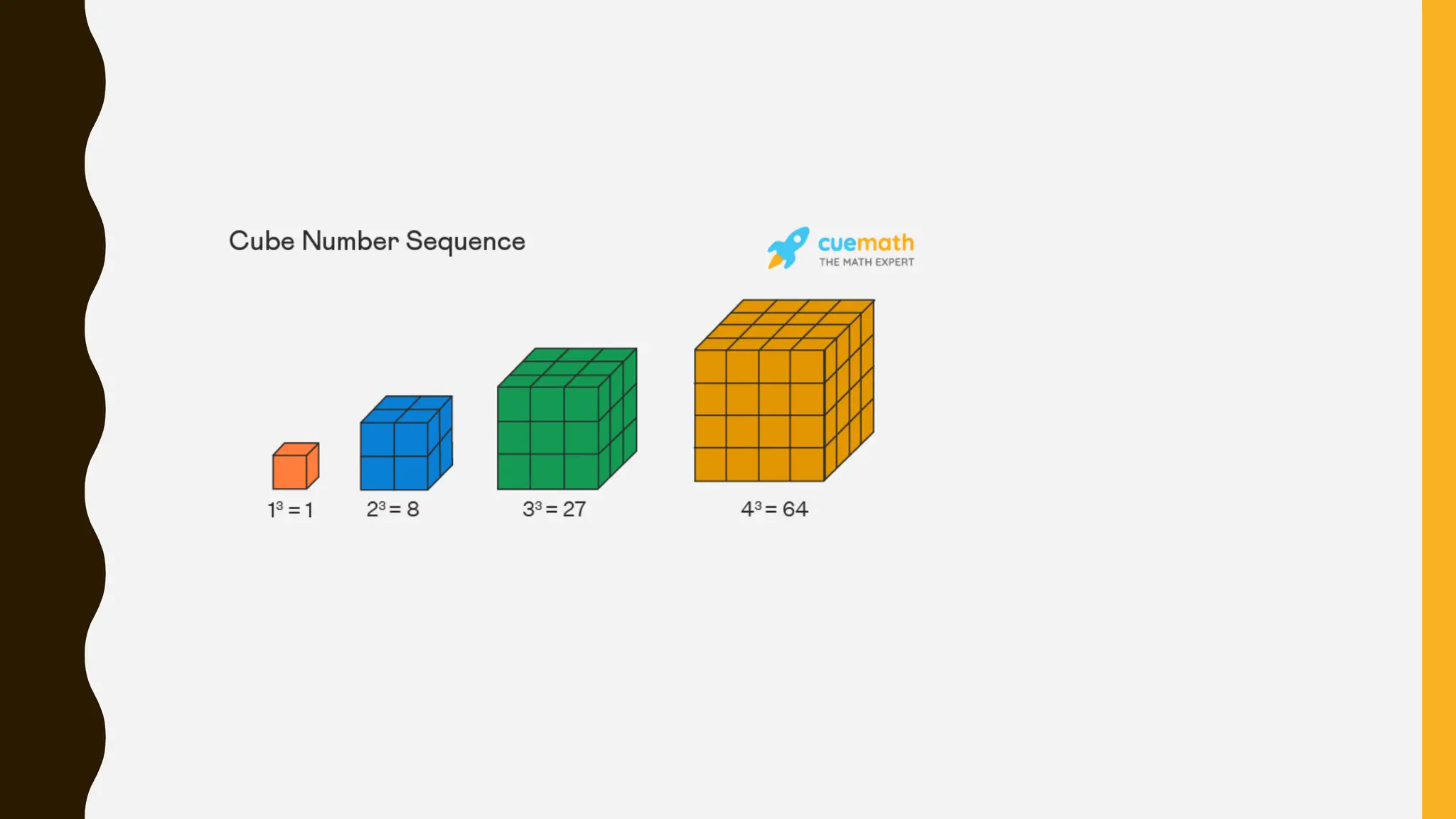
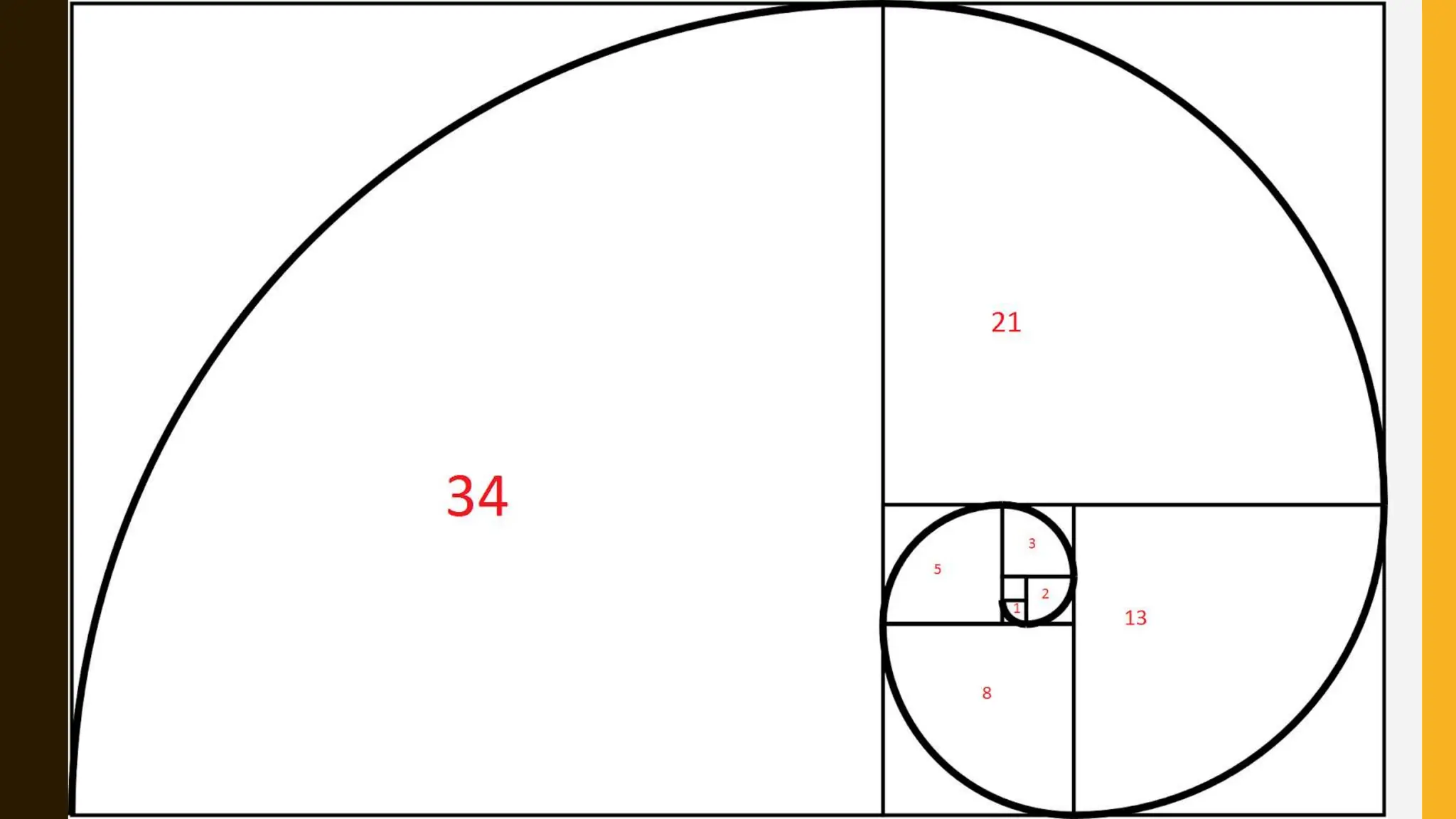
The document provides an overview of mathematical concepts including symmetry, sequences, functions, and problem-solving techniques. It explains various types of symmetry, different sequences (arithmetic, geometric, Fibonacci, etc.), and introduces mathematical terminology and expressions. Additionally, it describes reasoning methods, such as deductive and inductive reasoning, and illustrates problem-solving strategies with examples.

1. MATHEMATICS IN
THE MODERN
WORLD

2. PATTERNS
• It is defined as an organization of shapes and symbols distributed in regular interval.

3. SYMMETRY
Symmetry occurs when dividing a figure by two and will produce the two similar figures.
Symmetry can be reflective or rotational. For reflective symmetry, the right half and left
half of the figure should be mirror reflection of each other. For rotational symmetry, if
the figure rotates at its center, the figure should be the same as the original.

4. REFLECTIVE SYMMETRY

5. ROTATIONAL SYMMETRY

6. ORDER OF ROTATIONAL SYMMETRY
- it is defined by the number of times one can rotate a figure to get the same figure.
- if the shape is a regular polygon the order depends on the number of sides for
example:
A rectangle has an order of 2 but a square has an order of 4

7. FRACTALS
• Pattern of infinite iterations of the figure going in a loop.

8. SPIRAL
• Coiled pattern revolving about a center point.

9. WAVES
• Disturbances that carry energy

10. TESSALLATIONS
• Formed by repeating shapes over a plane.

11. CRACKS
• Openings formed to release stress

12. SPOTS AND STRIPES

13. SEQUENCE
• A list of numbers or elements arranged in a certain pattern.
• Each elements will be called terms
• It can be finite or infinite
• It can be ascending or descending order
• Each term can be evaluated through direct formula, relations from the preceding term
or table of values

14. ARITHMETIC SEQUENCE
• Each terms have a common difference between their preceding terms.
• 1,2,3,4,5… The sequence has a common difference of 1
• 2,4,6,8,10… The sequence has a common difference of 2
• 1,3,5,7,9… The sequence has a common difference of 2
• Equation for nth term
• 𝐴𝑛 = 𝐴1 + 𝑛 − 1 𝑑
• A1 is the first term and d is the common difference

15. GEOMETRIC SEQUENCE
• Each terms have a common ratio between their preceding terms.
• 1,2,4,8,16… The sequence has a common ratio of 2
• 1,4,16,64… The sequence has a common ratio of 4
• 𝐴𝑛 = 𝐴1𝑟𝑛−1
• r is the common ratio

16. HARMONIC SEQUENCE
• Each term is the reciprocal of the terms in an arithmetic sequence
• 1,1/2,1/3,1/4,1/5…(from 1,2,3,4,5)
• 1,1/4,1/7,1/10,1/13…(from 1,4,7,10,13)

17. QUADRATIC SEQUENCE
• The difference between the terms are arranged in arithmetic sequence
• 1 3 6 10 15
+2 +3 +4 +5
+1 +1 +1

18. Triangle Number Sequence
- the pattern of these sequence form
equilateral triangles
Square Number Sequence
- the pattern of these sequence form squares
Cube Number Sequence
- the pattern of these sequence form cubes

22. FIBONACCI SEQUENCE
• The next term of the sequence is the sum of the two preceding terms
F0 0
F1 1
F2 1
F3 2
F4 3
F5 5
F6 8
F7 13
F8 21
F9 34
F10 55
F11 89
F12 144
F13 233

23. GOLDEN RATIO
• The limit of the ratio of two consecutive terms of the Fibonacci Sequence.
• Approximately φ =1.618034
• Seen usually in nature
• Mathematical ratio describing aesthetically pleasing
• For Fibonacci Sequence, for the Nth term,
𝐹𝑁 =
𝜑𝑁
− (1 − 𝜑)𝑁
5

24. EXAMPLE
• For the 5th number = 5
𝐹5 =
1.6180345 − (1 − 1.618034)5
5
≈ 5
• For the 11th number = 89
𝐹11 =
1.61803411 − (1 − 1.618034)11
5
≈ 89

25. FIBONACCI SERIES SPIRAL
• Formed by drawing a spiral guided by stacking squares with dimensions from the
Fibonacci Sequence.
• Known for its aesthetic and symmetrical appearance

31. MATHEMATICAL LANGUAGE AND
SYMBOLS
• The study on Mathematical Language involves how to convey the ideas and solutions
of mathematics among others. The communication lies with how the idea is presented.
The presentation should be precise, concise and compelling.
• Mathematical symbols are the components used in forming these Mathematical
Language.

32. MATHEMATICAL EXPRESSION VS
MATHEMATICAL SENTENCES
• Both are layout of mathematical symbols but mathematical expression is simply a part
of a mathematical sentence. The mathematical expression does not give answers or
confirms the solution but mathematical sentence can.

33. SYMBOLS AND ITS INTERPRETATIONS
Symbols Interpretations
+ Addition(“plus”, ”add”, “increased”, “sum”, “more than”) or Positive number
- Subtraction(“minus”, “less”, “less than”, “decreased”, “difference”) or Negative number
÷ or / Division(“divide”, “ratio”, “quotient”)
× Multiplication(“times”, “multiply”, “product”)
= Equal(“equal”, “the same”)
>,<,> and < Inequality(“greater than”, “less than”, “greater than or equal” and “less than or equal”)
≈ and ≅ Approximately equal and congruent to respectively
% Percent(number times 100)
n√ nth root
{ }, [ ] and ( ) Braces, Brackets and Parenthesis respectively
Ab or A^b Exponent(“raised to”, “power of”)
|x| Absolute value
+ Plus - Minus
! Factorial
∑ Summation Sign

34. VARIABLES
• Variables are symbols used to represent some values.
• Usually in the form of an alphabet.

35. SET
• A collection of numbers or values written as a set-roster or set-builder
• ∈ means elements
• Set-Roster: X = {a, b, c}, X = {a, b, c, …} or X = {a, b, c, {d}}
• Set-Builder:
{X ∈ ℝ | a < X < b} : “X is set with an open interval between a and b”
{X ∈ ℝ | a < X < b} : “X is set with an closed interval between a and b”

36. Universal Set
-A collection of all elements from different set
Empty Set
-A set with no elements. Null or Void. Ø
Unit Set
- A set with one element
Complement of a set
- A set with elements not found from another set. AC
Subset
- A set of elements that are part of another set. ⊆
Union
- A collection of elements between two or more sets. ∪
Intersection
- A collection of the same elements between two or more sets. ∩

37. VENN DIAGRAM
• A Venn Diagram uses circles as representation of groups of elements for easy
understanding.
• Each circles convey a set. Each sets have their own category.
• The circles will be drawn in a universal set
• If there are overlapping circles, there is an intersection between the two or more set

39. FUNCTION
• A mathematical expression that convey that for every input, there is one designated
output
• Relations in mathematics establishes a connection between two elements usually for
input and output, x and y respectively for most time.
• y = f(x)
• Domain is a set of values that can be used as input for the function. It will be inserted
to the independent variable, “x”. The domain will result to a real value.
• Range is a set of values that are the output of the function if the domain is inserted. It
will be all possible value of the dependent variable, “y”.

40. BINARY OPERATIONS
• An action performed on two elements to produce a new elements.
• A + B = C
• A – B = C
• A x B = C
• A / B = C

41. LOGIC
• It is a study on statements or arguments to create valid interpretation
• Connectives are words or phrases that will connect two sentence to create a new
statement. Example: “and”, “or”, “if-then” and “if and only if”
• Proposition is a statement that can be evaluated as either true or false but it can’t be
both.

42. CONNECTIVES
• ~ or ¬ for negation( not true )
• ∧ for conjunction ( “and”).
• ∨ for disjunction (“ either or both”) and ⊻ for exclusive disjunction (“ either but not both”)
• -> for condition (antecedent and consequent, “if-then”)
• <-> for biconditional(“if and only if”)

43. NEGATION

44. CONJUNCTION

45. DISJUNCTION

46. EXCLUSIVE DISJUNCTION

47. CONDITIONAL

48. BICONDITIONAL

49. EXAMPLE
p: "The sky is cloudy".
q: "A triangle has three sides".
r: "It's raining".
s: "The bell is ringing".
t: "The dog is barking".
Write the statement:
a. ¬p ∧ q: The sky is not cloudy and a triangle has three sides
b. s→¬(t ∨ r): If the bell is ringing, then it's not true that the dog is barking or it's raining
c. p ⊻ s →t: If the sky is cloudy or the bell is ringing (but not both), then the dog is barking
d. q↔¬t: A triangle has three sides if and only if the dog is not barking

50. QUANTIFIERS
• These are words that describes the quantity of object
• Universal Quantifiers – a statement that proposes that a characteristic is true for all
elements like “for all” or “for every”. Denoted by ∀
• Existential Quantifiers- a statement that proposes that a characteristic is true for a
specific element or elements like “there exists” or “some”. Denoted by ∃

51. EXAMPLE
• ∀ x ((x < 0) -> (x3 < 0)): Every negative x has a negative cube
• ∃ x (x ∈ R -> (x3 < 0)) : Some value of x has a negative cube

52. PROBLEM SOLVING AND REASONING

53. DEDUCTIVE REASONING VS
INDUCTIVE REASONING
• The process of deductive reasoning is analyzing the general premises and draw
specific conclusion while in inductive reasoning predicts the conclusion
• Deductive reasoning
All catholic priests are men.
Padre Damaso is a catholic priest.
Therefore, Padre Damaso is a Man.
• Inductive reasoning
Jessie is not using his bike.
It is raining.
Therefore, Jessie won’t use his bike because it is raining

54. DEDUCTIVE REASONING
1.
All insects have exactly six legs.
Spiders have eight legs.
Therefore, spiders are not insects.
2.
Blue litmus paper turns red in the presence of acid.
The blue litmus paper turned red after I dropped some liquid on it.
Therefore, the liquid is acidic.

55. INDUCTIVE REASONING
1.
90% of the sales team met their quota last month.
Pat is on the sales team.
Pat likely met his sales quota last month.
2.
I get tired if I don't drink coffee.
Coffee is addictive.
I'm addicted to coffee.

56. POLYA’S PROBLEM SOLVING
TECHNIQUE
• Understand the Problem
• Devise a Plan
• Carry out the Plan
• Look Back

57. KAYLA IS 24 YEARS. KAYLA IS TWICE AS
OLD AS ERIN WHEN KAYLA WAS AS OLD
AS ERIN IS NOW. HOW OLD IS ERIN NOW?
• Understand the Problem
Given:
Kayla’s age now = 24
Kayla is 2x older than Erin when Kayla was the same age as Erin now
Asked:
The current age of Erin

58. • Devise a Plan
Use:
K = Kayla’s age now
E = Erin’s age
Y = Years past when Kayla’s age was the same as Erin’s age
Y years ago,
K – Y = E
K – Y = 2(E – Y)
Now
K = 24

59. • Carry out the plan
K = 24
K – Y = E
K – Y = 2(E – Y)
E = 2E – 2Y
2Y = 2E – E
E = 2Y
K – Y = E
24 – Y = 2Y
3Y = 24
Y = 8
E = 2Y = 2(8) = 16 y/o

60. • Look Back
8 years ago,
Kayla’s age = 24 – 8 = 16 same as Erin’s current age
Erin’s age = 16 – 8 = 8 so Kayla is twice as old

61. WHAT TIME AFTER 3 O’CLOCK WILL THE
HANDS OF THE CLOCK ARE TOGETHER FOR
THE FIRST TIME?
Given:
It is after 3 o clock
Asked:
What time will both clock arms be together for the first time after 3 o clock
Both clock arms move at different rate. The minute hand completes a revolution for 60
minutes while the hour arm completes a revolution for 720 minutes. To determine the
position of the arms, we use angles as in radians. So one revolution is 2π. The rates for
the two arms are:
π/30 for the minute arm
π/360 for the hour arm

62. The rates will be multiplied to how many minutes have passed. The next consideration is
the initial positions of each arms. Let us use the 12th hour mark as reference. The minute
will start at the reference but the hour arm started at the 3rd hour mark so an initial
position of π/2 is considered for the hour arm. The difference between the positions of
both arms presents the angle between them.
Use:
T = time passed in minutes
Pm = minute arm position
Ph = hour arm position
B = angle between the two arms
𝑃𝑚 =
𝜋
30
𝑇
𝑃ℎ =
π
360
𝑇 +
𝜋
2
𝐵 = 𝑃𝑚 − 𝑃ℎ

63. 𝐵 =
𝜋
30
𝑇 −
π
360
𝑇 +
𝜋
2
Since the two arms should be together B = 0
0 =
𝜋
30
𝑇 −
π
360
𝑇 +
𝜋
2
𝜋
30
𝑇 =
π
360
𝑇 +
𝜋
2
𝜋
30
𝑇 −
π
360
𝑇 =
𝜋
2
𝑇
𝜋
30
−
π
360
=
𝜋
2
𝑇 = 16.36 𝑚𝑖𝑛𝑠
16.36 mins have passed from 3:00 when the two arms were together. So the time is
3:16.36

64. As the two clocks show here the incident occurs between 3:16 to 3:17

65. A PUMP CAN PUMP OUT WATER FROM A
TANK IN 11 HOURS. ANOTHER PUMP CAN
PUMP OUT WATER FROM THE SAME TANK
IN 20 HOURS. HOW LONG WILL IT TAKE
BOTH PUMPS TO PUMP OUT WATER IN
THE TANK?
Given:
Pump 1 can do its job for 11 h
Pump 2 can do its job for 20 h
Asked:
How long can the two pump do its job together

66. The rate of pump 1 is 1 job for 11 hour(1/11) while the rate of pump 2 is 1 job for 20
h(1/20). Combining the two rates will lessen the time. The solution will be the sum of the
two rates multiplied to the time consumed by the two pumps and equate it to one job.
Use:
T = time consumed by the two pumps to do one job
1
11
+
1
20
𝑇 = 1
𝑇 =
1
1
11
+
1
20
𝑻 = 𝟕 𝒉𝒐𝒖𝒓𝒔
The time is faster than both pump individually.