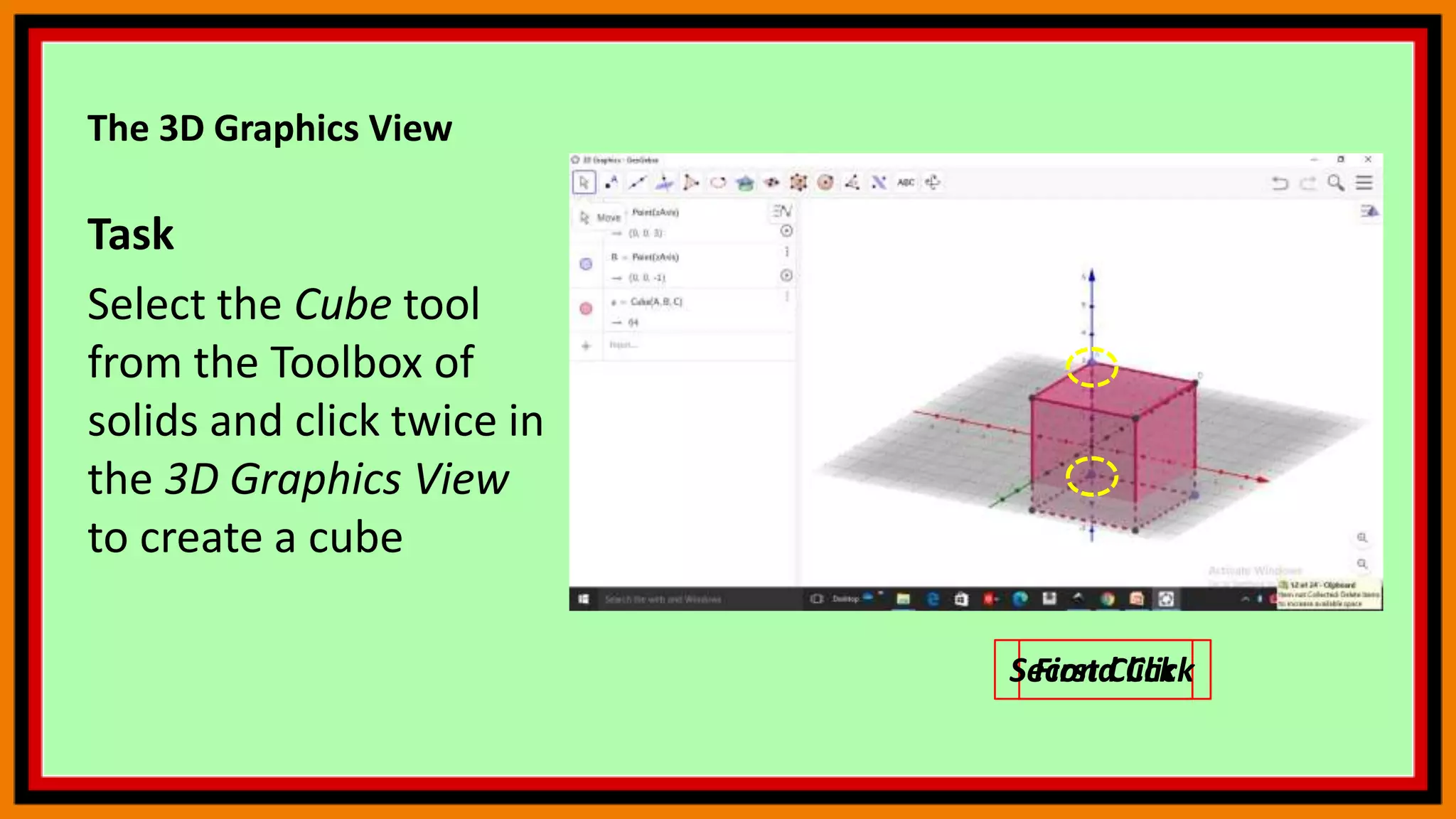
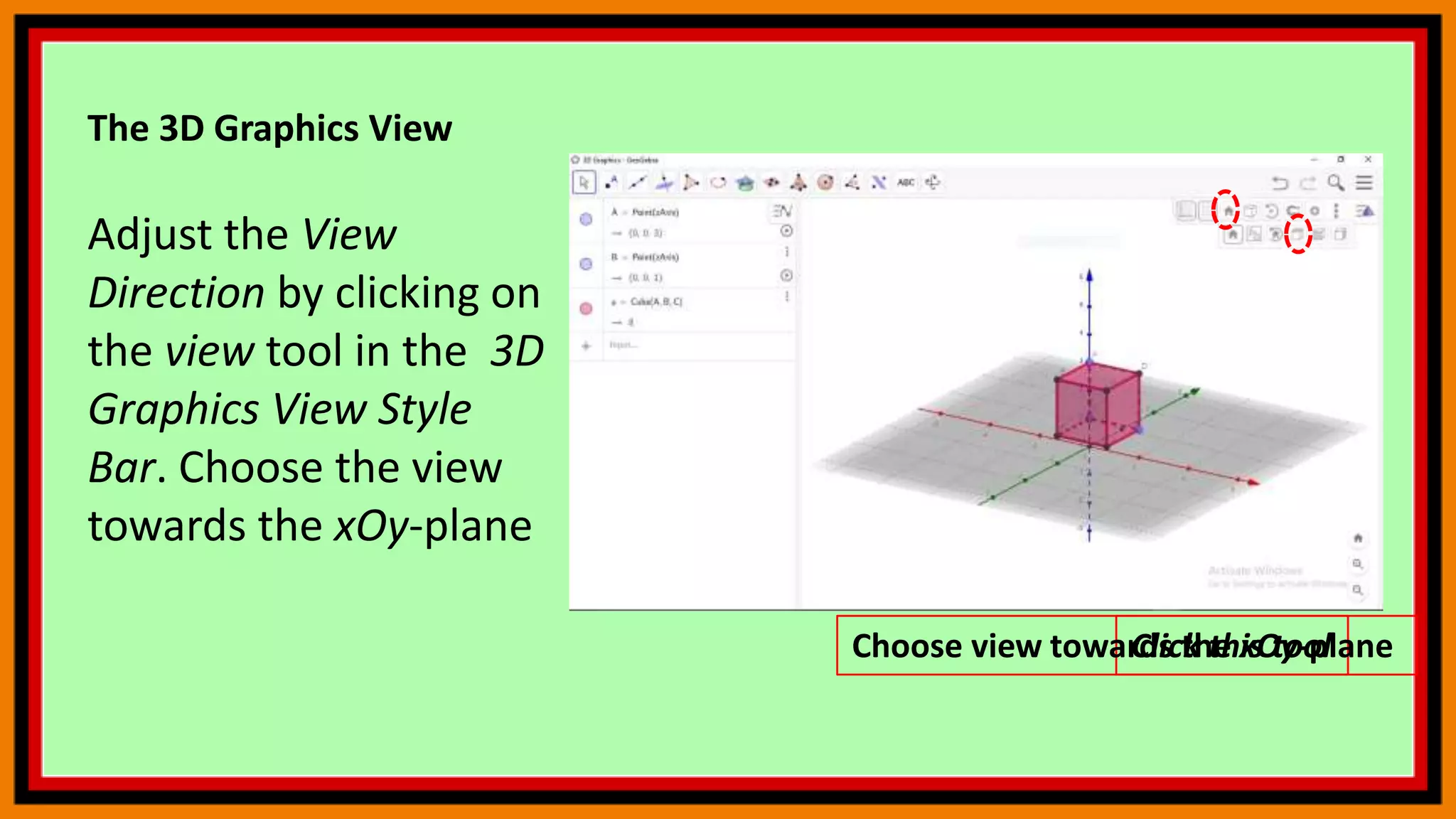
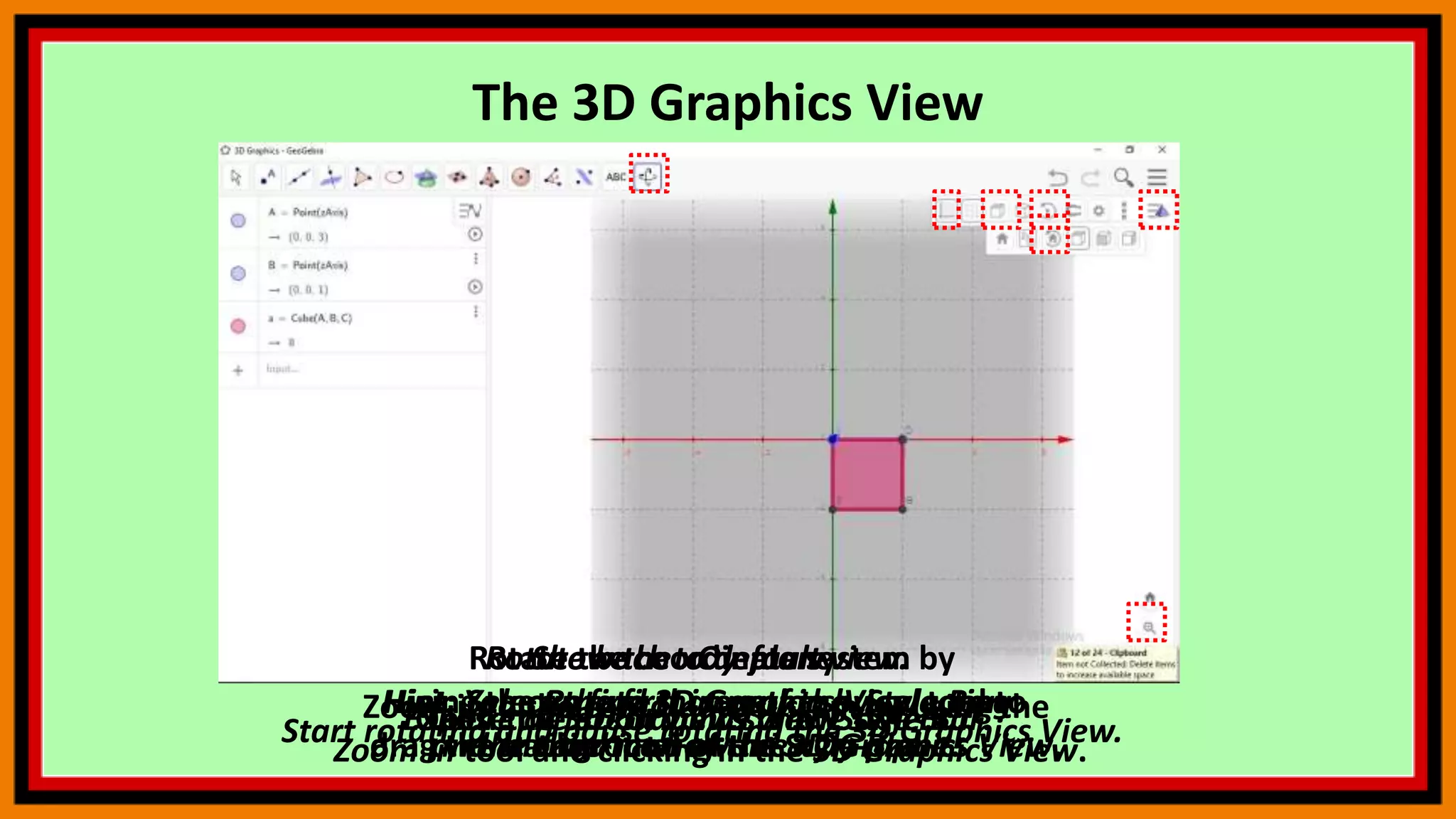
The document discusses 3D graphics in GeoGebra, including how to customize the 3D graphics view, find the intersection of a plane and line, calculate the distance between two lines, graph functions of two variables, and use commands. It provides examples of constructing various geometric objects in the 3D view and exploring their relationships, as well as tips for navigating commands in GeoGebra.

1. 3D Graphics

2. Contents
 3D Graphics Perspective
 Customizing the 3D Graphics View
 Intersection of a Plane and a Line
 Distance between two lines
 Functions of two variables
 Commands

3. 3D Graphics Perspective
The 3D Graphics Perspective includes the 3D Graphics
View and the Algebra View. By default, the coordinate axes
and the xOy-plane are shown in the 3D Graphics View.
Furthermore, the 3D Graphics View Toolbar and the Undo /
Redo buttons in the top right corner are displayed.

4. The 3D Graphics View
Using the construction
Tools available in the
3D Graphics View
Toolbar you can create
geometric
constructions in
the 3D Graphics View.
Geometric Construction
3D Graphics View Toolbar

5. The 3D Graphics View
Select any
construction Tool from
the 3D Graphics View
Toolbar and read the
appearing Tooltip to
find out how to use
the selected Tool.
Tooltip

6. The 3D Graphics View
Note: Any object you
create in the 3D
Graphics View also has
an algebraic
representation in
the Algebra View.
Algebraic representation

7. The 3D Graphics View
Example
Select the Sphere with
Center through Point tool
and click twice in the 3D
Graphics View. The first
click creates the center
point while the second
click creates a sphere and
a point on the sphere. First Click
Second Click

8. The 3D Graphics View
Task
Select the Cube tool
from the Toolbox of
solids and click twice in
the 3D Graphics View
to create a cube
First Click
Second Click

9. The 3D Graphics View
Select the Move tool and
change the position of the
points and the size of the
cube by dragging them
with the pointer.
Hint: By clicking on a point you
can switch between moving the
point parallel to the x-y-plane or
parallel to the z-axis.

10. The 3D Graphics View
Open the 3D Graphics
View Style Bar by
clicking the button in
the top right corner.
3D Graphics View Style Bar

11. The 3D Graphics View
Adjust the View
Direction by clicking on
the view tool in the 3D
Graphics View Style
Bar. Choose the view
towards the xOy-plane
Click this tool
Choose view towards the xOy-plane

12. The 3D Graphics View
Rotate the 3D Graphics
View back to default
view.
Click here to return to default view

13. The 3D Graphics View
Select the Rotate 3D
Graphics View tool and
drag the background of
the 3D Graphics View
with your pointing
device.
Hint: Alternatively you can
right-drag the background of
the 3D Graphics View to rotate
the coordinate system.
Rotate 3D Graphics View tool

14. Customizing the 3D Graphics View
You can customize the 3D Graphics View according to the
mathematical topic you want to work with. The basic setup
can be changed using the 3D Graphics View Style Bar (e.g.
display of coordinate axes, xOy-plane, grid).
Note: In addition, the Settings provide more options to
customize the 3D Graphics View.
Customize the 3D Graphics View by following the instructions
below.

15. The 3D Graphics View
Open the 3D Graphics View Style Bar
Show the xOy-plane.
Hint: Select the first icon of the Style Bar
and choose to show the xOy-plane.
Explore different views of the object.
Start rotating and pause rotating the 3D Graphics View.
Rotate back to default view.
Hint: You can find that option by selecting
the third icon of the Style Bar.
Zoom into the coordinate system by using the
Zoom In tool and clicking in the 3D Graphics View.
Close the 3D Graphics View Style Bar.
Rotate the coordinate system by
using the Rotate 3D Graphics View tool to
drag the background of the 3D Graphics View.

16. Intersection of a Plane and a Line
Do It Yourself
Task 1
Intersect a plane and a line in the 3D Graphics View of
GeoGebra to create the intersection point.

17. The 3D Graphics View
1.Enter p: x + y = z into the Input Bar in the Algebra View
and hit the Enter key to define a plane p.
2.Create two points A and B by entering A = (3, 4, 3) and B =
(-4, -2, -1) into the Input Bar and hitting the Enter key
after each input.
3.Select the Line tool from the 3D Graphics Toolbar and
click on the points A and B respectively to create the
line a through both points.

18. The 3D Graphics View
4.Select the Intersect tool. Then, click on the plane and the line
to create the intersection point C.
5.Use the Move tool to change the position of the points A and
B. What happens to the intersection point if the line is parallel
to the plane, or if both points lie within the plane?
Hint: By clicking on a point you can switch between moving the
point parallel to the x-y-plane or parallel to the z-axis.

19. Distance between two lines
Task 2
Find out the shortest distance between two lines.
1. Select the Line tool and create two arbitrary lines f and g.
2.Select the Parallel Line tool and create a parallel line h of g through
point A. Create point E on the parallel line h using the Point on
Object tool.
3.Create a plane a through the points A, B and E using the Plane
through 3 Points tool.
4.Create a point F on line f using the Point on Object tool.
5.Create a perpendicular line i to plane a through point F using the
Perpendicular Line tool.

20. Distance between two lines
6.Create a plane b through line i and line f using the Plane tool.
7. Create intersection point G of line g and plane b using the Intersect
tool.
8.Create perpendicular line j to plane a through point G using the
Perpendicular Line tool.
9.Create intersection point H of line j and line f using the Intersect
tool.
10. Create the shortest distance between line f and line g using the
Segment tool and create a segment between points G and H.
11.Enhance your construction using the Style Bar.

21. Functions of two variables
Task 3
Graph the function f(x, y) = sin(x + y) and observe the created
surface by moving a point along the function graph.
1.Enter f(x, y)= sin(x + y) into the Input Bar and hit the Enter key
to define a function f.
2.Create the point A by entering A = (2, 0, 0) into the Input Bar
and hitting the Enter key.
3.Enter Segment(A, (x(A), y(A), f(x(A), y(A)))) into the Input Bar to
create a segment g.

22. Functions of two variables
Graph the function f(x, y) = sin(x + y) and observe the created
surface by moving a point along the function graph.
4.Create the point B by entering B = (x(A), y(A), f(x(A), y(A))) into
the Input Bar.
5.Exploration: Use the Move tool to change the position of point
A. You can also change the function f by entering another
function: e.g. f(x, y)= sin(x) + sin(y)
6. Enhance your construction using the Style Bar.

23. Commands
In order to locate
commands faster, click
near the + sign and
then click help button.

24. Press Help
Click the + sign on any
of the topics you
would like to visualize.

25. Press Help
Click the subtopic you
would like to visualize.
Choose any one of these depending on
the parameters you have

26. Press Help
Click the subtopic you
would like to visualize.
Enter object and Vector

27. Press Help
Sometimes you can
just type the
command and choose
the right command
among the popups.
Type
Choose Here

28. END
Try as many problems as possible. Practice
GeoGebra by following commands in the
GeoGebra Manual posted earlier. You can also
find many applets and resources on the GeoGebra
website.
Next: .