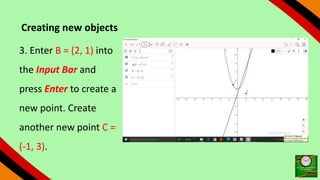
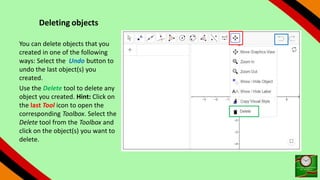
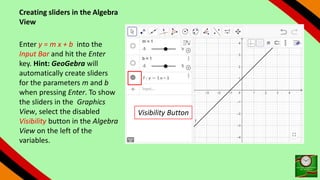
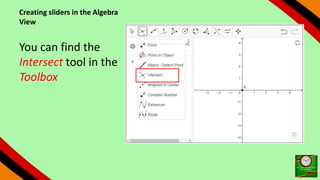
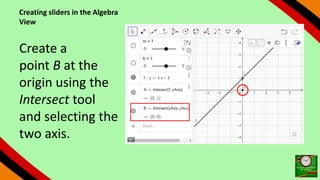
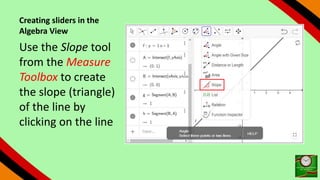
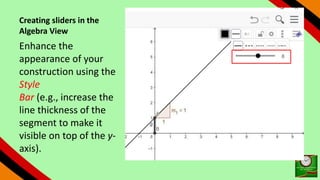
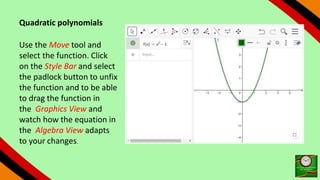
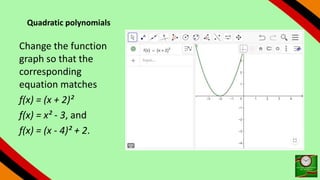
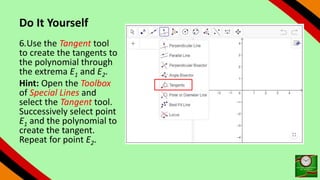
This document provides instructions for using GeoGebra to graph and explore functions and polynomials. It discusses how to create points, lines, and functions by entering their equations or using tools. It also describes how to create sliders to manipulate the parameters of linear and quadratic equations, and explores how changing the parameters affects the graphs. The document demonstrates finding roots, extrema, and drawing tangents for cubic polynomials with adjustable parameters.

2. Contents
Functions and Coordinates
Parameters of linear equations
Quadratic polynomials

3. Functions and Coordinates
Creating new objects
You can create new objects
(e.g. points, lines, functions)
by either using the Graphics
Tools provided in the Toolbar,
or by entering their equations
and coordinates into the Input
Bar.
Task
• Enter the following
equations and
coordinates into the Input
Bar to graph functions
and points.

4. Creating new objects
1. Enter the equation
y = 3x + 1 into the
Input Bar and press
the Enter key.
2. Enter the function
g(x) = x² + 2 into the
Input Bar and press
the Enter key.

5. Creating new objects
3. Enter B = (2, 1) into
the Input Bar and
press Enter to create a
new point. Create
another new point C =
(-1, 3).

6. Creating new objects
4. Select the Line
tool from the
Toolbar and click
twice in the
Graphics View or
on the two existing
points B and C to
create a line.

7. Virtual Keyboard
Hint: Click on the
keyboard icon to open
a Virtual Keyboard
whenever you want to
use it to enter
mathematical
expressions.

8. Modifying existing objects
You can drag existing objects in
the Graphics View, or change
their equations and coordinates
in the Algebra View.
1. Select an object in the
Algebra View to directly
change its equation or
coordinates, or redefine it
2.Select the Move tool and drag
objects in the Graphics View to
change their position.

9. Deleting objects
You can delete objects that you
created in one of the following
ways: Select the Undo button to
undo the last object(s) you
created.
Use the Delete tool to delete any
object you created. Hint: Click on
the last Tool icon to open the
corresponding Toolbox. Select the
Delete tool from the Toolbox and
click on the object(s) you want to
delete.

10. Parameters of linear equations
Creating sliders in the Algebra View
When you enter a letter different from
x and y in the Input Bar, which hasn't
been defined previously, GeoGebra
will create a slider in the Algebra
View after pressing Enter.
Note: You can display the slider in the
Graphics View by selecting the
disabled Visibility button next to the
number in the Algebra View.
Task
Graph a linear equation y =
m x + b which parameters
can be modified using
sliders. Display the slope of
the corresponding line and
visualize the y-intercept.

11. Creating sliders in the Algebra
View
Enter y = m x + b into the
Input Bar and hit the Enter
key. Hint: GeoGebra will
automatically create sliders
for the parameters m and b
when pressing Enter. To show
the sliders in the Graphics
View, select the disabled
Visibility button in the Algebra
View on the left of the
variables.
Visibility Button

12. Creating sliders in the
Algebra View
Create the intersection
point A between the line
and the y-axis. Hint: You
may either use the
Intersect tool you can find
in the Toolbox for points by
selecting the two objects,
or use the
command Intersect(f,
yAxis).

13. Creating sliders in the Algebra
View
You can find the
Intersect tool in the
Toolbox

14. Creating sliders in the Algebra
View
Create a
point B at the
origin using the
Intersect tool
and selecting the
two axis.

15. Creating sliders in the Algebra
View
Select the Segment
tool from the
Toolbox for lines and
create a segment
between
points A and B by
selecting both
points.

16. Creating sliders in the Algebra
View
Hint: Alternatively,
you can use the
command
Segment(A, B) as
well.

17. Creating sliders in the Algebra
View
Hide points A and B
by clicking on the
corresponding
enabled Visibility
buttons on the left
of their coordinates
in the Algebra View.

18. Creating sliders in the
Algebra View
Use the Slope tool
from the Measure
Toolbox to create
the slope (triangle)
of the line by
clicking on the line

19. Creating sliders in the
Algebra View
The slope
(triangle) of the
line

20. Creating sliders in the
Algebra View
Enhance the
appearance of your
construction using the
Style
Bar (e.g., increase the
line thickness of the
segment to make it
visible on top of the y-
axis).

21. Change a slider's position in the Graphics View
By default, the position of a
slider is absolute on screen.
This way, you can change its
value using the Move tool
without moving the whole
slider accidentally. To change
the position of a slider you
can either...
1.select the Slider tool and
drag the slider to a new
position.
2. right-drag the slider to
change its position (use the
right key of your mouse if
available).

22. Quadratic polynomials
Task
Explore the impact of parameters
on a quadratic polynomial by either
moving the function graph or
changing its equation.
Type f(x) = x^2 into the Input Bar
and hit the Enter key. Which shape
does the function graph have?

23. Quadratic polynomials
Use the Move tool and
select the function. Click
on the Style Bar and select
the padlock button to unfix
the function and to be able
to drag the function in
the Graphics View and
watch how the equation in
the Algebra View adapts
to your changes.

24. Quadratic polynomials
Change the function
graph so that the
corresponding
equation matches
f(x) = (x + 2)²
f(x) = x² - 3, and
f(x) = (x - 4)² + 2.

25. Quadratic polynomials
Task
Select the equation of the polynomial. Use the
keyboard to change the equation to f(x) =
3x². How does the function graph change? Repeat
changing the equation by typing in different
values for the parameter (e.g. 0.5, -2, -0.8, 3).

26. Parameters of a polynomial
Task
Graph a cubic polynomial f(x) =
a x³ + b x² + c x + d whose
parameters can be changed
using sliders. In addition,
display the roots and local
extrema with their
corresponding tangents.
Explore the construction...

27. Do It Yourself
1. Enter f(x) = ax³ + bx² + cx + d into the Input Bar and
hit the Enter key. Hint: GeoGebra will automatically
create sliders for the parameters a, b, c, and d.
2.Show the sliders in the Graphics View by selecting the
disabled Visibility buttons on the left of the
corresponding entries in the Algebra View.

28. Do It Yourself
3. Use the sliders in the Graphics View to change the values of
the parameters with the Move tool to a = 0.2, b = -1.2, c = 0.6
and d = 2.
4. Enter R = Root(f) into the Input Bar to display the roots of the
polynomial and automatically name themR1, R2 and R3.
5. Enter E = Extremum(f) to display the local extrema of the
polynomial.

29. Do It Yourself
6.Use the Tangent tool
to create the tangents to
the polynomial through
the extrema E1 and E2.
Hint: Open the Toolbox
of Special Lines and
select the Tangent tool.
Successively select point
E1 and the polynomial to
create the tangent.
Repeat for point E2.

30. Do It Yourself
7.Systematically change the values of the sliders using
the Move tool to explore how the parameters affect
the polynomial.

31. END
NEXT TOPIC:
continue…