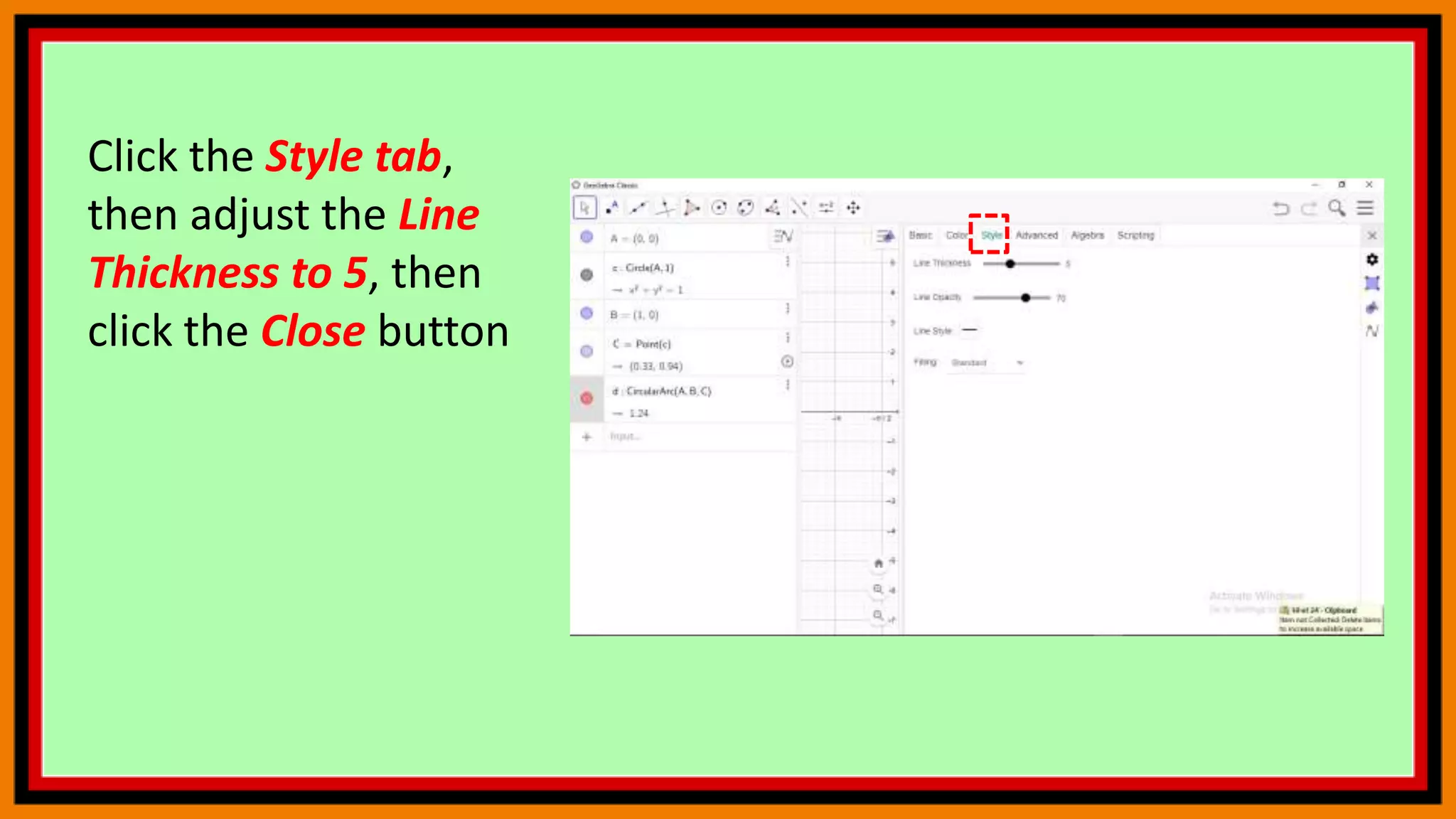
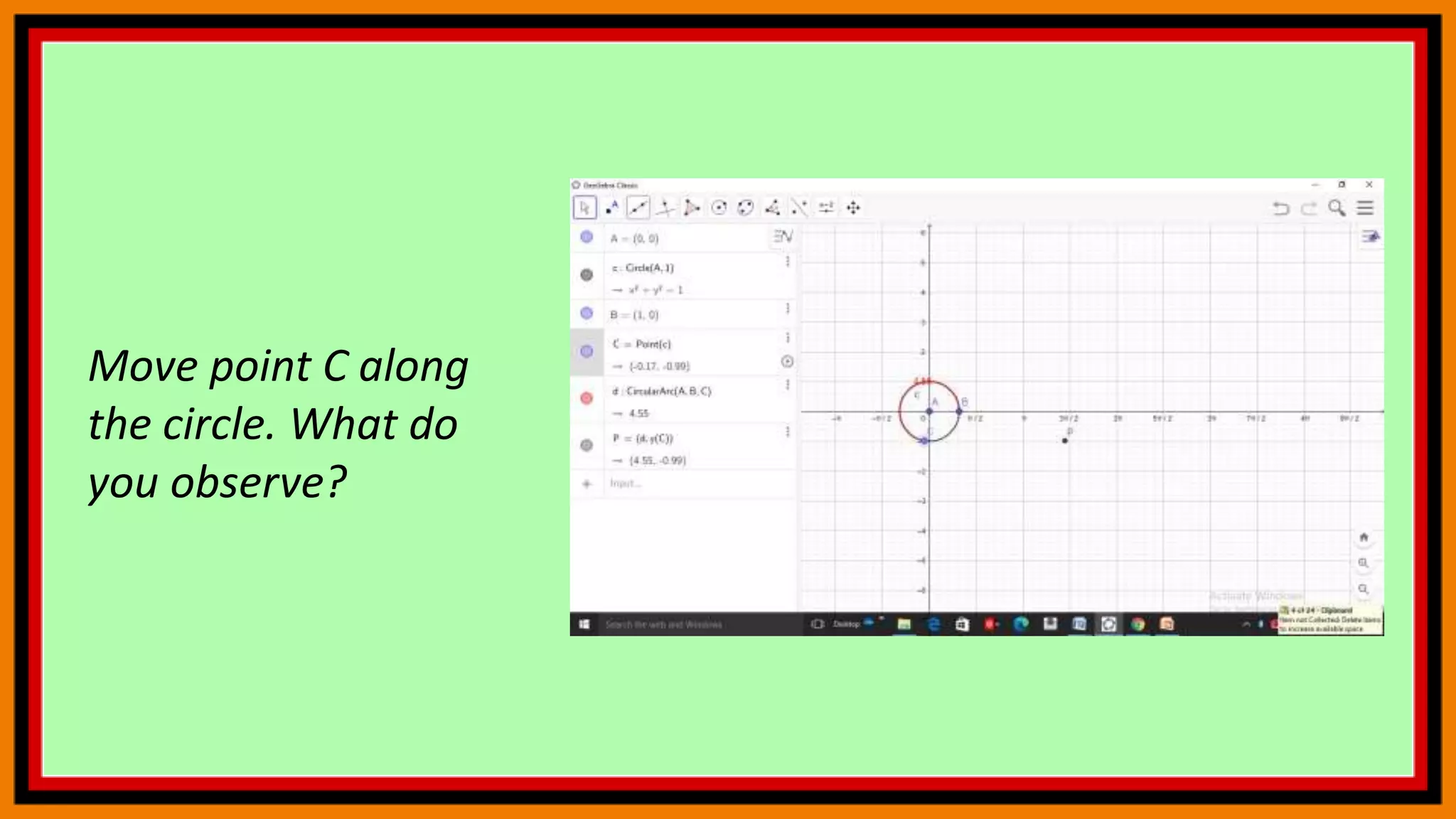
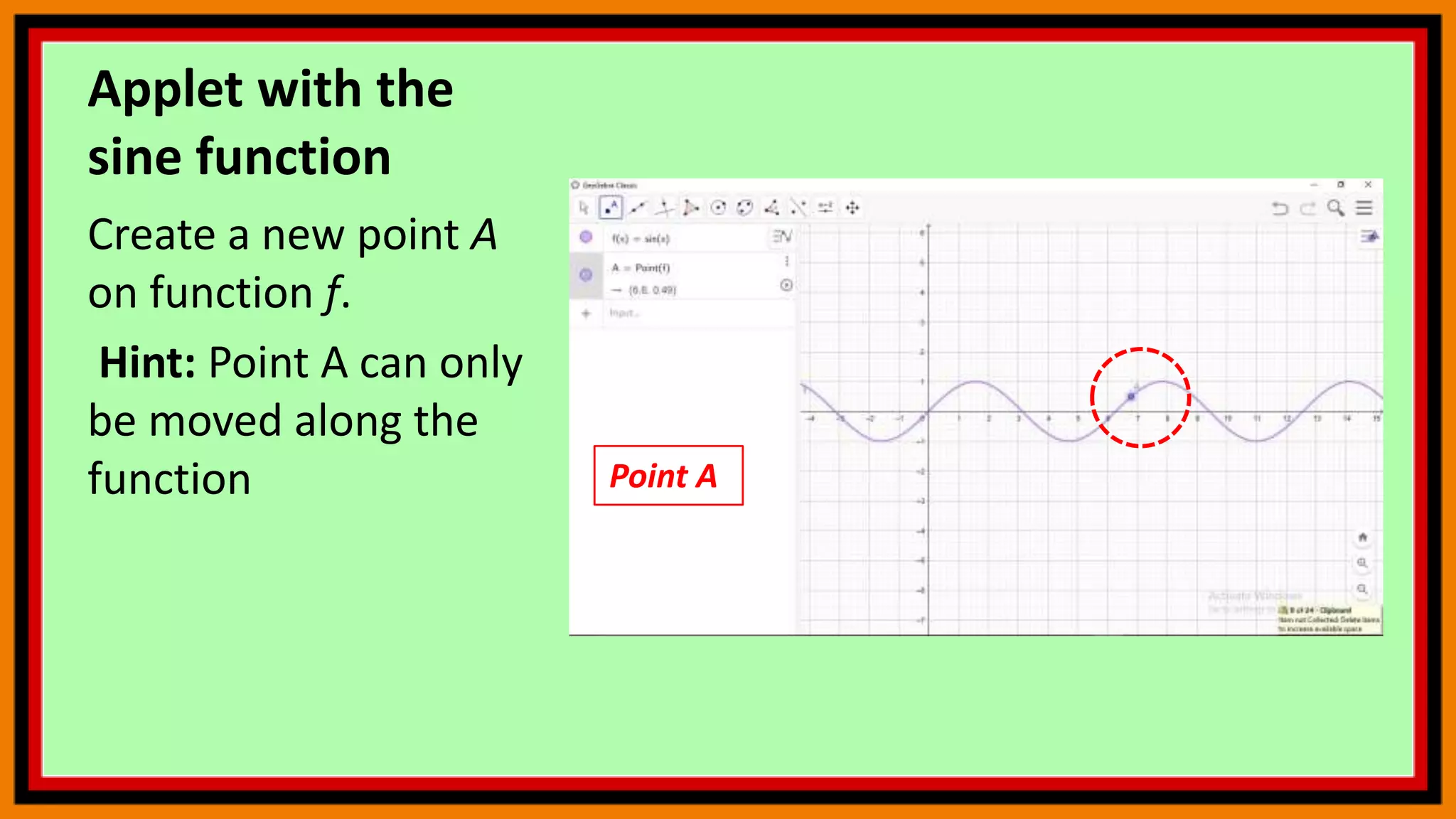
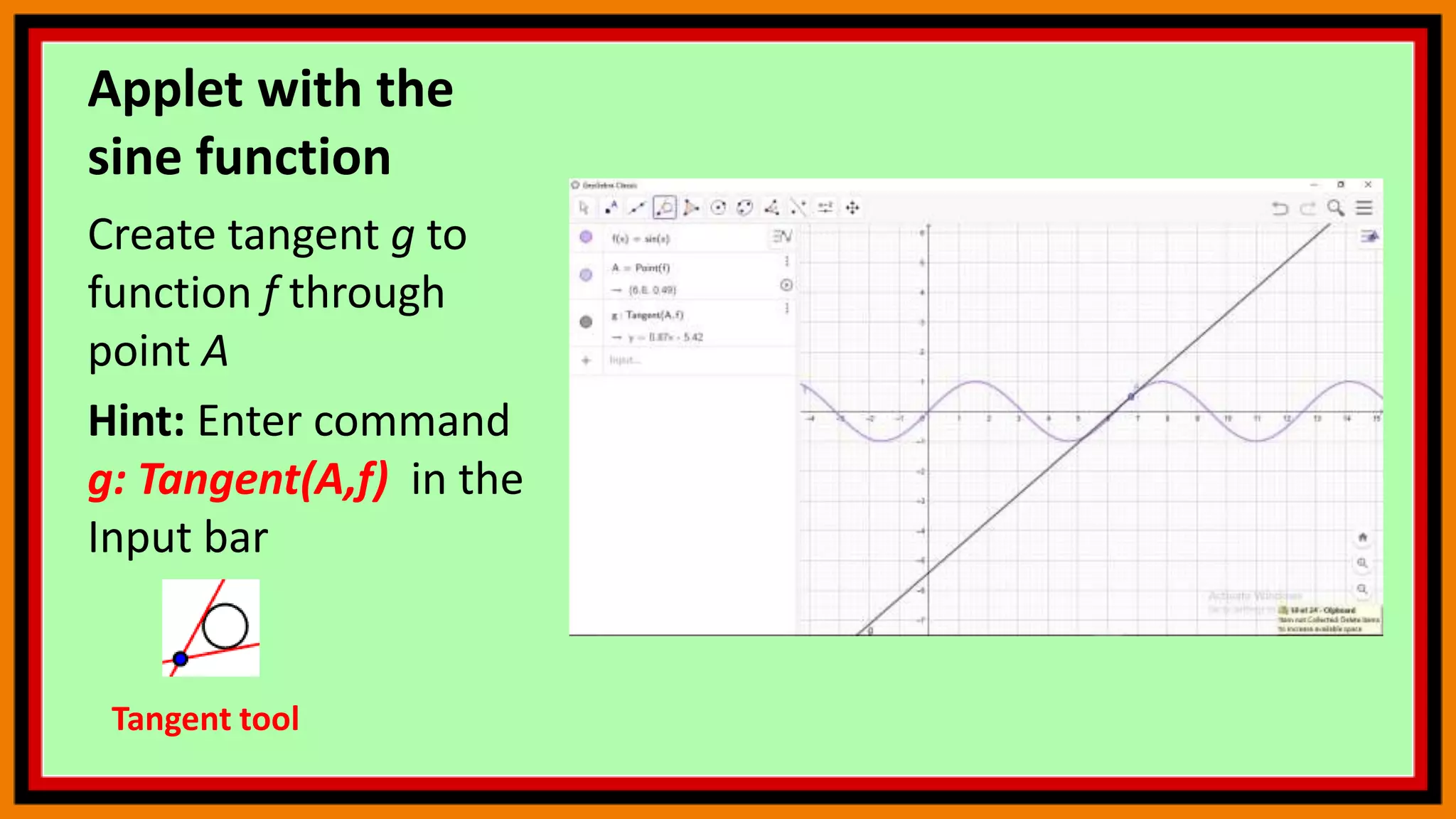
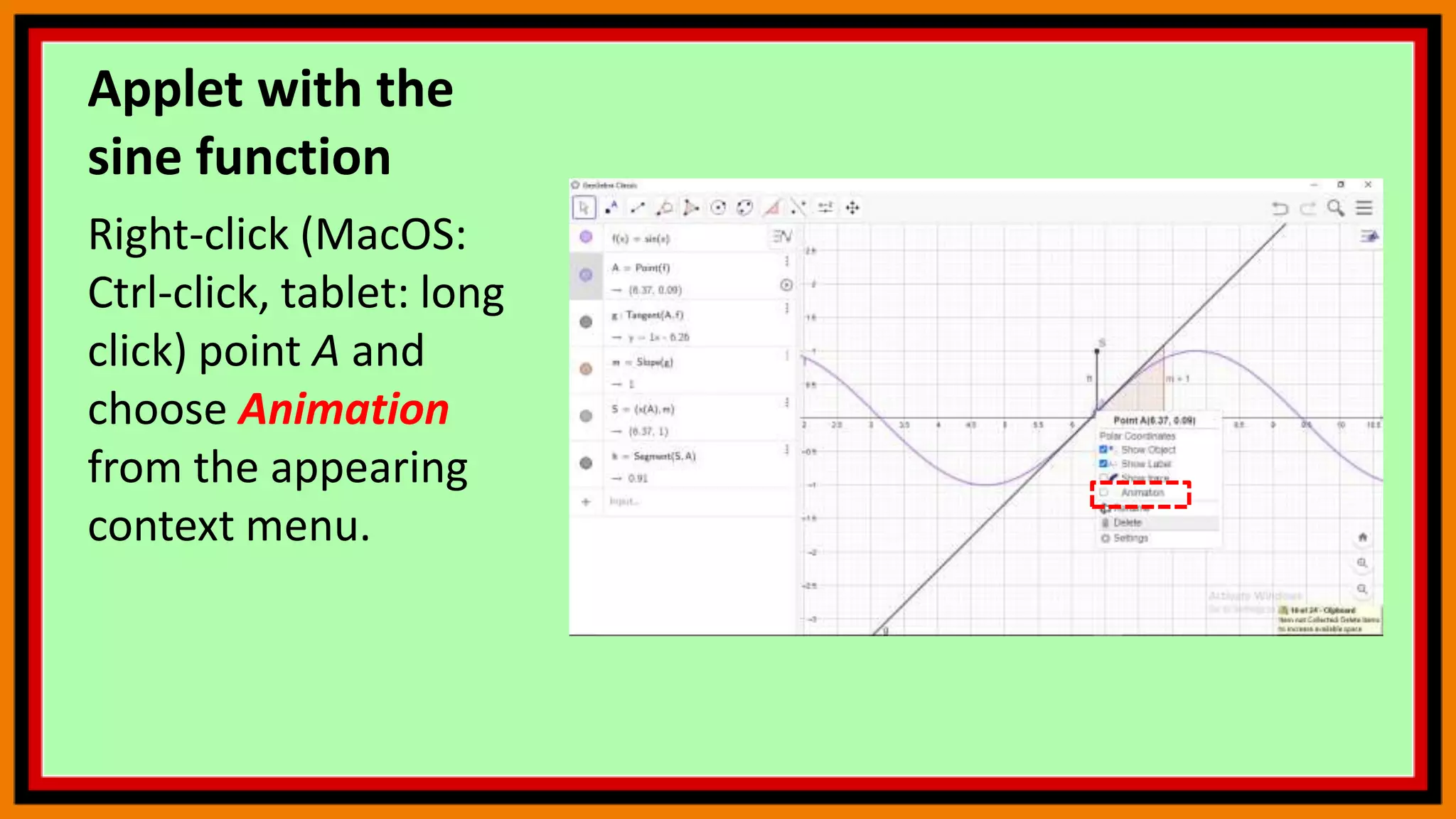
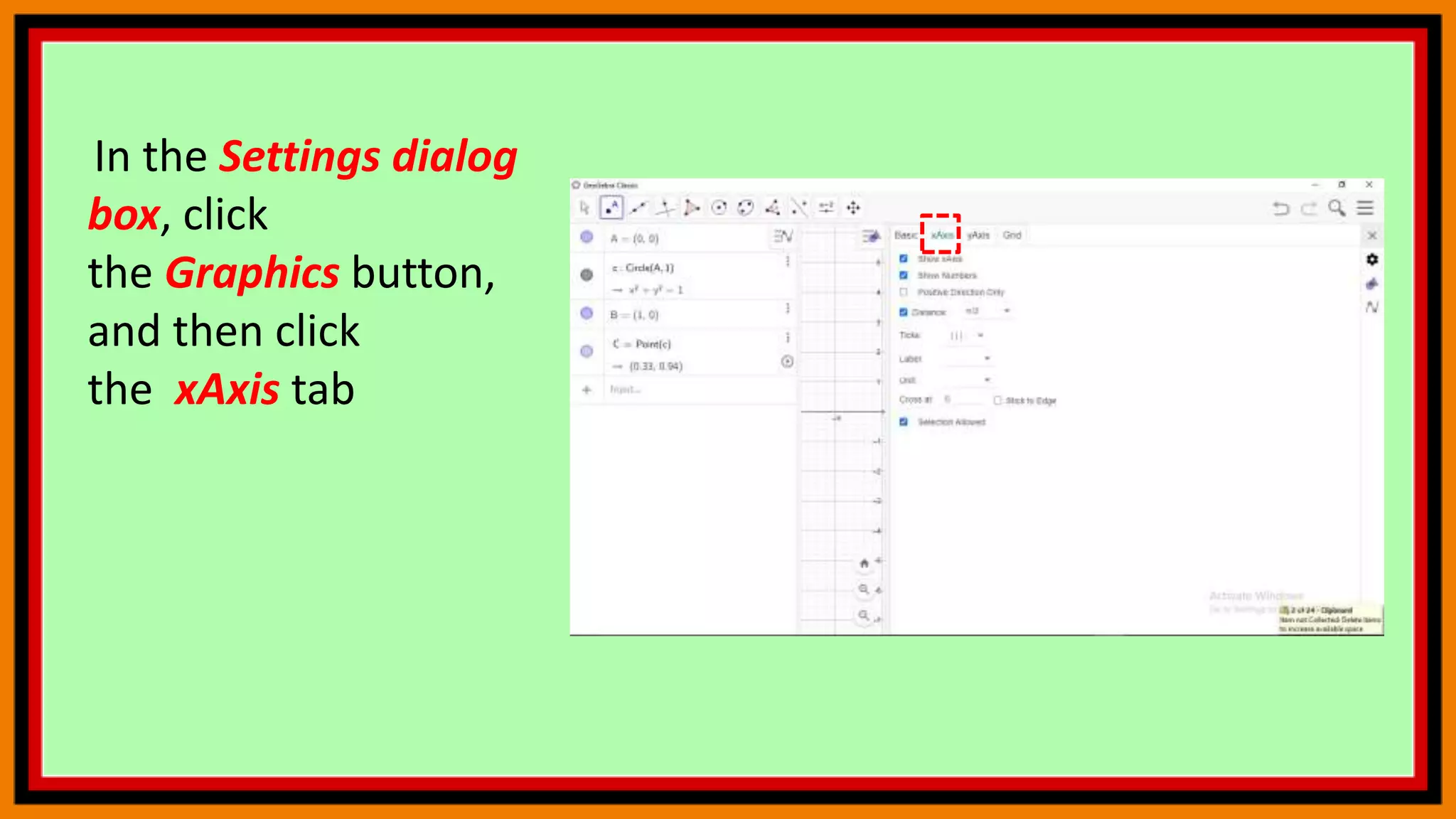
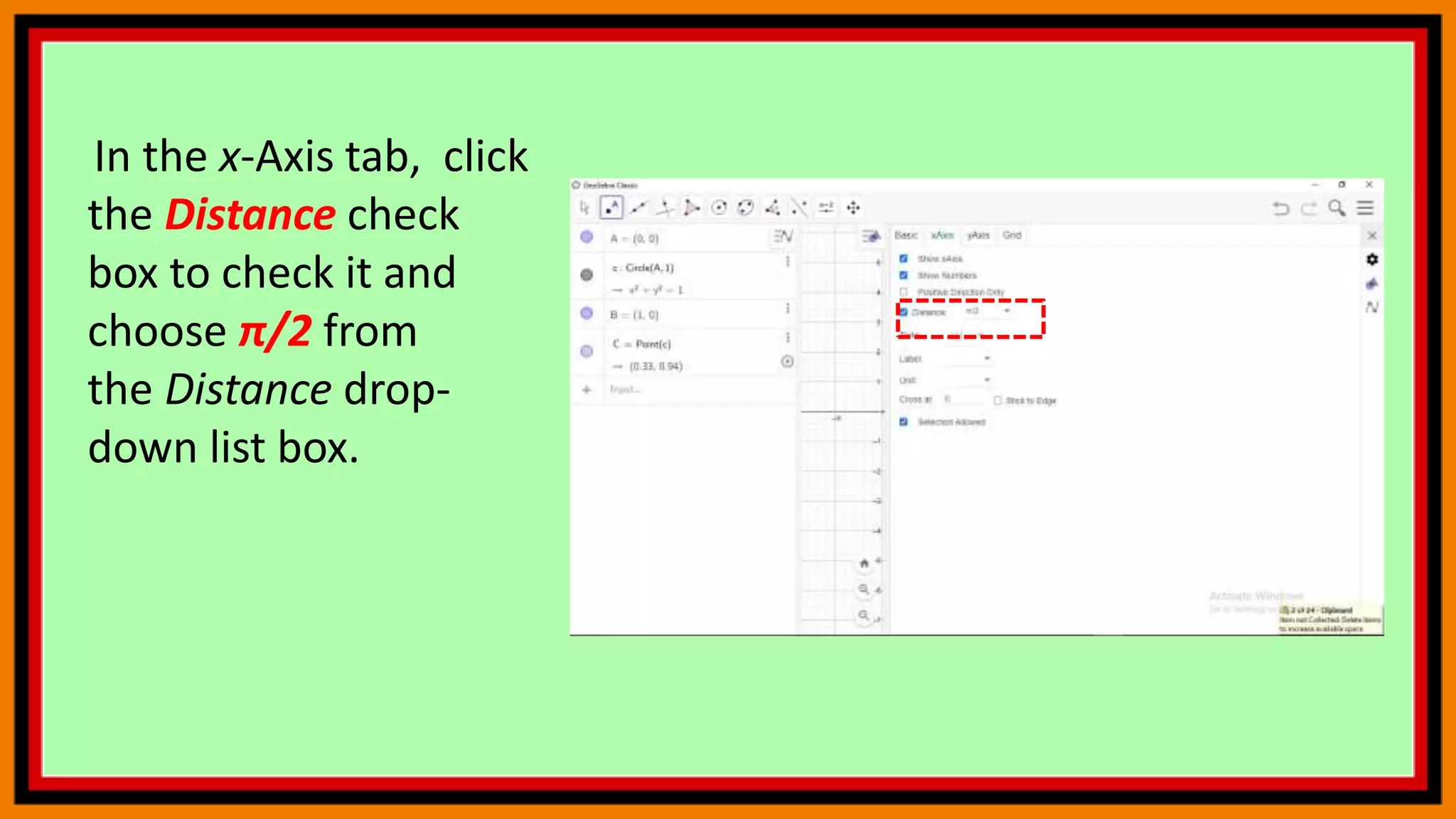
The document discusses deriving the sine function and tracing trigonometric functions in GeoGebra. It provides steps to create an applet that graphs the sine function and its derivative by tracing the slope of tangents. Additionally, it describes how to construct a circle, point, and arc in GeoGebra that will trace the sine and cosine functions as another point is moved along the circle. The steps change the x-axis to radians and activate tracing to observe the paths of the points tracing sine and cosine.

2. Contents
Derivation of Sine
Tracing the Graphs of Trigonometric
Functions

3. Derivation of Sine
Task
Create an applet with the sine function and graph its
derivative through the slope of the tangent in each point.

4. Applet with the
sine function
Enter the function
f(x) = sin(x)

5. Applet with the
sine function
Create a new point A
on function f.
Hint: Point A can only
be moved along the
function Point A

6. Applet with the
sine function
Create tangent g to
function f through
point A
Hint: Enter command
g: Tangent(A,f) in the
Input bar
Tangent tool

7. Applet with the
sine function
Create the slope of
tangent g using the
Slope tool
Slope tool

8. Applet with the
sine function
Define point
S = (x(A), m).
Hint: x(A) gives you
the x-coordinate of
point A

9. Applet with the
sine function
Connect points A and
S using a segment
Segment tool

10. Applet with the
sine function
Turn on the trace of
point S.
Hint: Right-click point
S (MacOS: Ctrl-click,
tablet: long click) and
select Show Trace

11. Applet with the
sine function
Right-click (MacOS:
Ctrl-click, tablet: long
click) point A and
choose Animation
from the appearing
context menu.

12. Applet with the
sine function
Hint: An Animation
button appears in the
lower left corner of
the Graphics View. It
allows you to either
pause or continue an
animation

13. Applet with the
sine function
Right-Click on the
Graphics View and
Select Graphics... .

14. Applet with the
sine function
Select tab xAxis and
change the unit to 

15. Tracing the Graphs of Trigonometric Functions
Just like in the previous tutorial, in this tutorial, we use
the Input bar to create mathematical objects particularly a
circle, an arc, and a point that traces the sine and cosine
function. In doing the tutorial, we learn the following:
 use the GeoGebra keyboard commands to construct various
geometric objects
 use the GeoGebra trace function
 change the interval of the x-axis

16. Open GeoGebra and
be sure the Algebra &
Graphics view is
displayed
(Perspectives menu).
To create point A at
the origin, type A =
(0,0) in the Input
bar and press the
ENTER key on your
keyboard

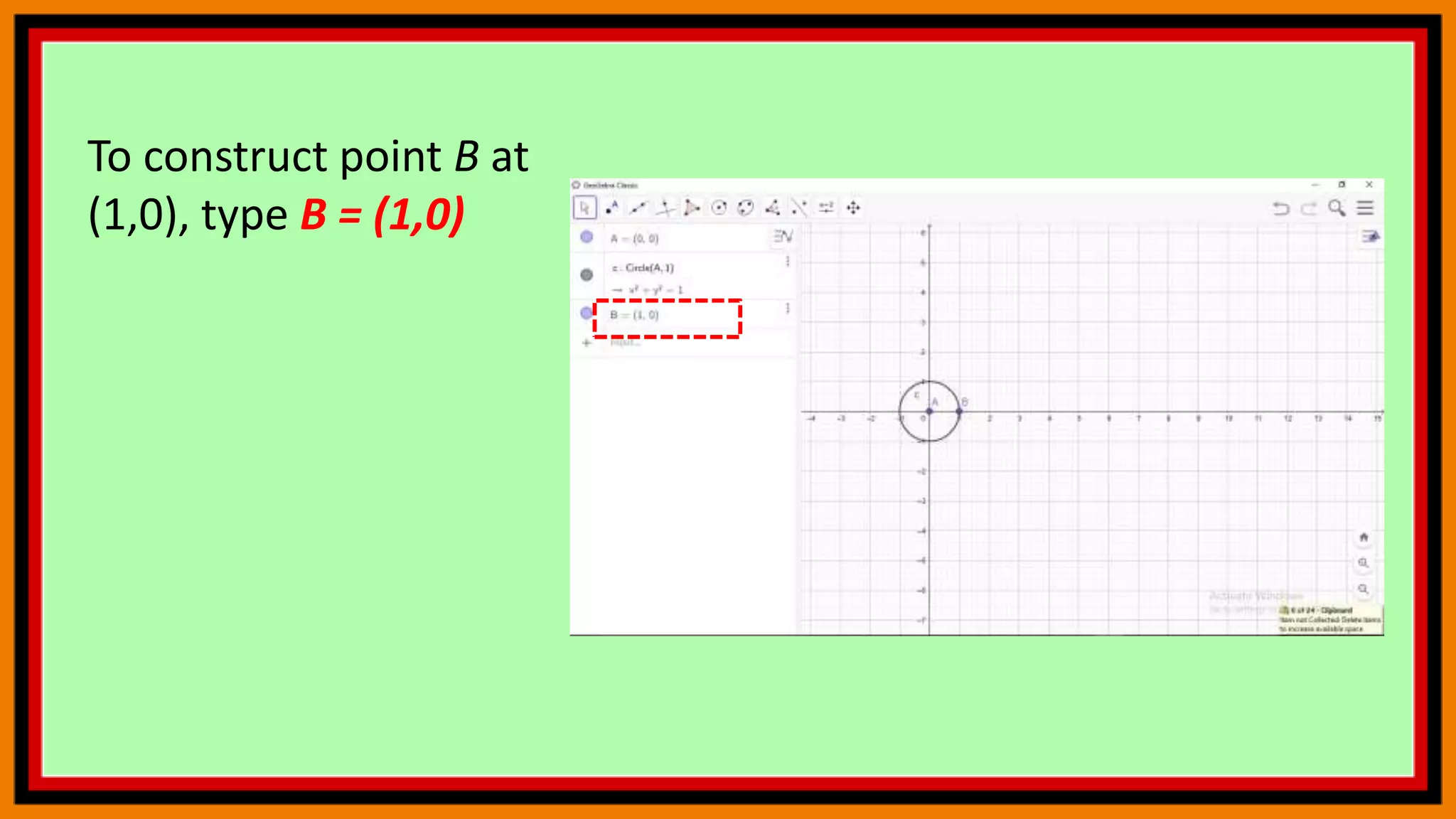
17. Next, to construct a
circle with
center A and radius 1,
type circle[A,1] in
the Input Bar and
press the ENTER key
on your keyboard

18. We fix point A to
prevent it from being
accidentally moved. To
fix the position of
point A, right click on
point A, and then
click Object Properties
from the context
menu.

19. This will display
the Preferences dialog
box.
In Basic tab of
the Preferences dialog
box, click the Fix
Object check box to
check it, then close
the window

20. To construct point B at
(1,0), type B = (1,0)

21. Fix the location of
point B

22. To construct
point C on the
circumference of
the circle, click
the New Point tool
and click on the
circumference of
the circle

23. We now change the
interval of the x-axis
from 1 to π/2. To do
this, right
click Graphics from
the context menu

24. In the Settings dialog
box, click
the Graphics button,
and then click
the xAxis tab

25. In the x-Axis tab, click
the Distance check
box to check it and
choose π/2 from
the Distance drop-
down list box.

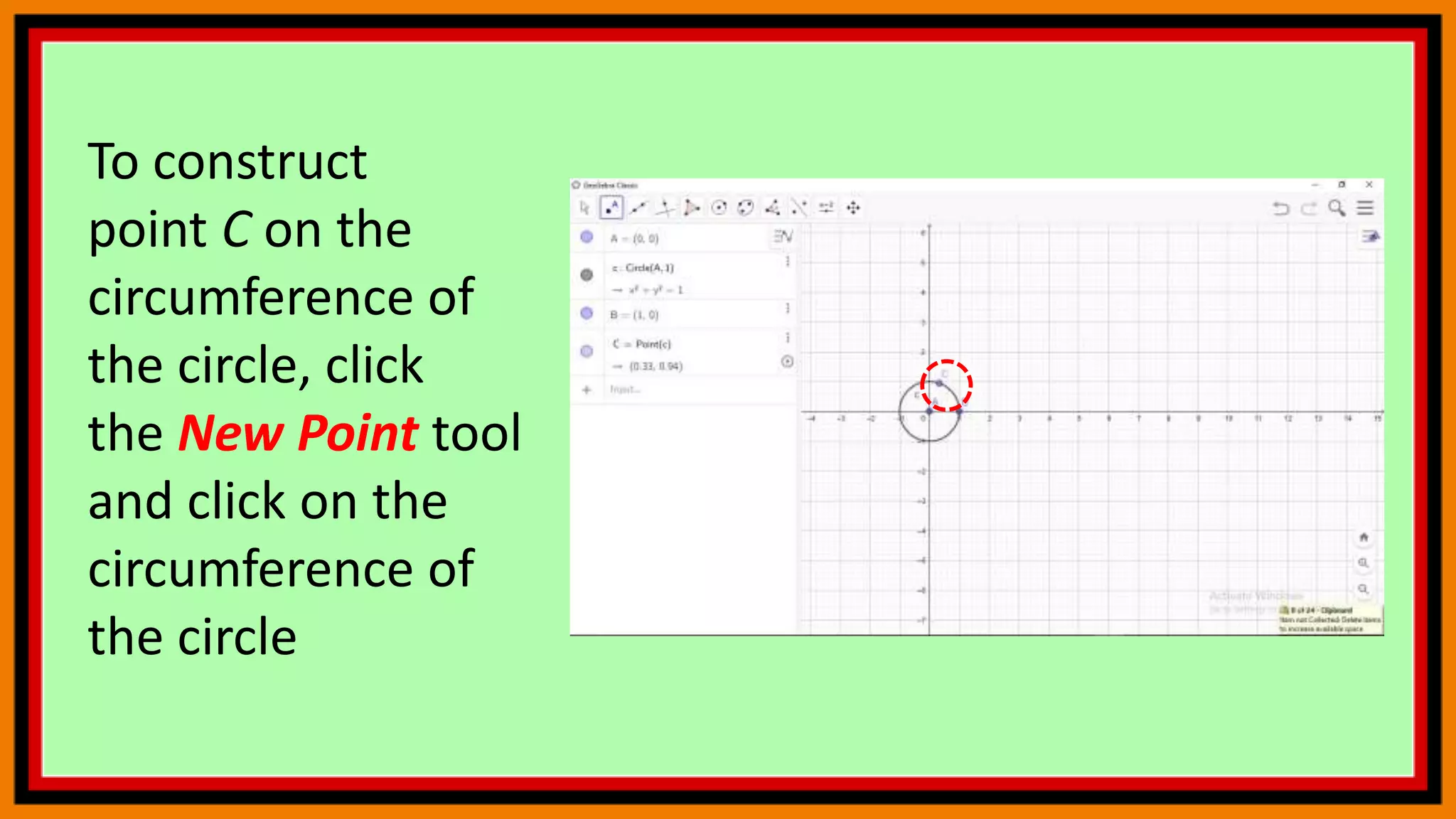
26. Now we create
arc BC of circle with
center A starting
from B and going
counterclockwise
to C. To do this, type
circularArc[A, B, C]

27. Right click the
arc BC, then
click Object Properties
to display
the Preferences
window.

28. In the Preferences
window, choose
the Basic tab.

29. Be sure that the Show
label check box is
checked and
choose Value from the
drop-down list box.
This will display the
length of arc BC

30. Next, we change the
color of the arc to
make it visible. Click
the Color tab and
choose red (or any
color you want except
black) from the color
palette

31. Click the Style tab,
then adjust the Line
Thickness to 5, then
click the Close button

32. Next, to construct the
point that will trace
the sine wave, we
construct an ordered
pair (d,y(C)) where d is
the arc length
of BC and the y(C) y-
coordinate (or the
sine) of point C. To do
this, type P = (d,y(C)).

33. Move point C along
the circle. What do
you observe?

34. To trace the path
point P, right click
on P and click Trace
on from the context
menu

35. Now, move point C
along the
circumference of the
circle and see the path
of P

36. To create point Q that
will trace the cosine
wave, type Q = (d,x(C))

37. Activate the trace
function of point Q

38. Now, move point C
along the
circumference of the
circle and observe the
path of point Q. What
do you observe?

39. Do It Yourself
Graph the other four functions namely
tangent, contangent, secant and
cosecant functions

40. END
NEXT TOPIC:
continue…