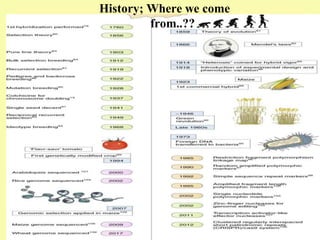
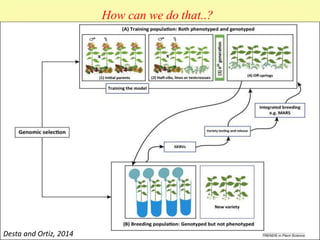
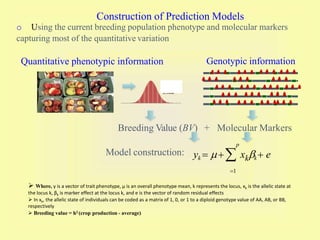
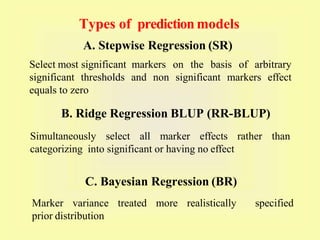
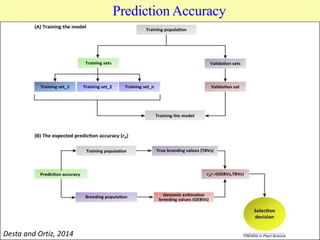
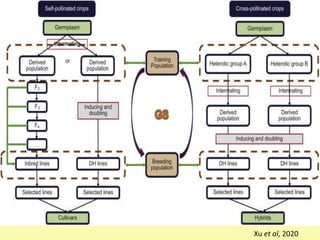
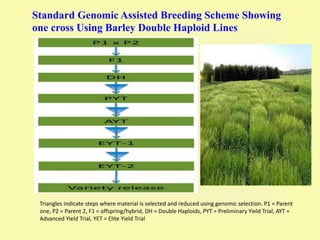
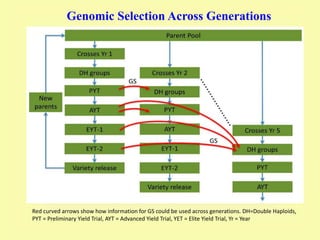
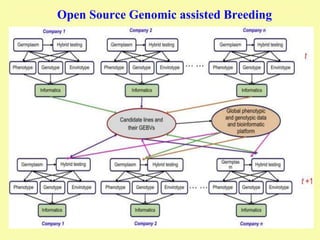
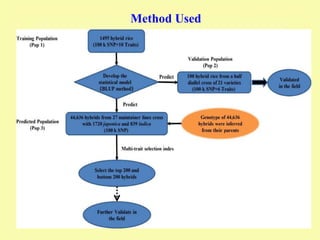
This document discusses genomic selection in plants. It begins with an introduction to genomic selection and its history. Genomic selection uses dense genetic markers and phenotypic data from a reference population to develop prediction equations that can then be applied to other populations to estimate genomic breeding values without additional phenotyping. The document outlines the steps involved, including preparing phenotypic and genotypic data, constructing prediction models, fitting and evaluating models, and applying genomic selection in breeding programs. It provides examples of software used and factors that affect prediction accuracy. The document concludes with two case studies, one on genomic selection for hybrid rice and another on genomic selection to improve wheat grain quality.

1. Genomic Selection in Plants
PRAKASH N. TIWARI
PhD Scholar
Biotechnology Centre
JNKVV, Jabalpur

2. Presentation Overview
 Introduction (GS)
 Preparation of phenotypic and
genotypic data
 Construction of GS model
 Fitting and evaluation of GS model
 GS in breeding programs
 Case study

3. History; Where we come
from..??

4. Why Genomic selection
important to turn on now..??
Relatively slow progress via phenotypic
selection
Large cost of phenotyping
Limited throughput (plot area, time, people)
By the MAS, major success is only achieved
with the qualitative traits
Meet the challenge of feeding 9.5
billion @ 2050

5. GENOMIC SELECTION (GS)
• Proposed by Meuwissen et al. (2001)
• Genomic selection is based on estimation of detailed
associations between a very dense set of genetic markers and
phenotypes on a selected group of plants (the
reference population)
• The resulting prediction equations are then applied to SNP
genotyped rest population to estimate their genomic
breeding value (GEBV), without the need of additional
phenotypes (Oldenbroek, 2015)

6. Desta and Ortiz, 2014
How can we do that..?

7. Preparing
Phenotypic and Genotypic Data

8. • Phenotypic data often comes messy and unbalanced, and needs to be pre-
processed prior to be used in fitting any GS model
• Often it is a two-stage process: 1) obtain single observation foreach
genotype as mean, 2) fit a GS model
• Most genotypic data used in GS comes as large datasets with thousand of
SNPs
• Molecular matrix for GBLUP is prepared by inversing molecular-based
genomic matrix (GA)

9. Construction of Prediction Model

10. Range: -0.0190 ~ 0
Mean: -0.00021
SD: 0.00380
Model construction:
Breeding Value (BV) + Molecular Markers
p
o Using the current breeding population phenotype and molecular markers
capturing most of the quantitative variation
Quantitative phenotypic information Genotypic information
Construction of Prediction Models
 Where, y is a vector of trait phenotype, μ is an overall phenotype mean, k represents the locus, xk is the allelic state at
the locus k, βk is marker effect at the locus k, and e is the vector of random residual effects
 In xk, the allelic state of individuals can be coded as a matrix of 1, 0, or 1 to a diploid genotype value of AA, AB, or BB,
respectively
 Breeding value = h2 (crop production - average)
yk   xkk e
1

11. Select most significant markers on the basis of arbitrary
significant thresholds and non significant markers effect
equals to zero
A. Stepwise Regression (SR)
B. Ridge Regression BLUP (RR-BLUP)
Simultaneously select all marker effects rather than
categorizing into significant or having no effect
C. Bayesian Regression (BR)
Marker variance treated more realistically specified
prior distribution
Types of prediction models

12. Fitting and Evaluating a GS Model

13. SOFTWARE FOR GBLUP
 GA Matrix Preparation
1. TASSEL (Bradbury et al. 2007)
2. rr-BLUP R package (Endelman 2011)
3. GenoMatrix (Nazarian and Gezan, 2015)
 Performs quality control of marker data
 Constructs and manipulates GA and Arelationship matrices
 Fitting GBLUPModel
• ASReml-R package (Butler et al. 2007)
 Package that fits linear mixed models to moderately large data
sets
 Useful for analysis of large and complex dataset
 Reads GA (or its inverse)

14. Genomic Selection

15. Desta and Ortiz, 2014
Prediction Accuracy

16. Validation of a GS model fit
Validation is often done by:
1. Partitioning the data: Validation with the same data
is expected to give the best results
2. Cross-validation: Use different portions of the data
3. True-validation: Use data from a different trial,
another season, or data from the next generation of
breeding
4. K-fold Cross-Validation: By randomly selecting
(1/k) of the observations at random as the training
population and the remaining (1-1/k) are used for
validation

17. Critical factors that affect the accuracy of GS
1. Selection of the training and validation populations: Relatedness
2. Number of SNPs available: High
3. The size of breeding population: High
4. Number of individuals to be evaluated and its replication: High
5. Heritability of a trait: High
6. Trait architecture (additive/non-additive, Mendelian/Fisherian)
7. Level of Genotype-by-Environment effects: Low
8. GS method used for fitting: E.g. GBLUP, Bayes B

19. Xu et al, 2020

20. Standard Genomic Assisted Breeding Scheme Showing
one cross Using Barley Double Haploid Lines
Triangles indicate steps where material is selected and reduced using genomic selection. P1 = Parent
one, P2 = Parent 2, F1 = offspring/hybrid, DH = Double Haploids, PYT = Preliminary Yield Trial, AYT =
Advanced Yield Trial, YET = Elite Yield Trial

21. Genomic Selection Across Generations
Red curved arrows show how information for GS could be used across generations. DH=Double Haploids,
PYT = Preliminary Yield Trial, AYT = Advanced Yield Trial, YET = Elite Yield Trial, Yr = Year

22. Open Source Genomic assisted Breeding

23. Case Study

24. Case Study 1

25. Method Used

26. Result
 Using a breeding index combining 10 traits, they identified the top and
bottom 200 predicted hybrids
 This will increase the opportunity of selecting true superior hybrids
with
 SNP genotypes of the training population and parameters estimated
from this training population are available for general uses and further
validation in genomic hybrid prediction of all potential hybrids
generated from all varieties of rice

27. Case Study 2

28. Method Used
TS; Truncated selection, OCS; Optimized contributution selection

29. Result
 Genomic selection with TS and OCS led to a 25 ± 12% and 34 ± 6.4%
increase in wheat grain fructan content, respectively
 Although positive gains from selection were observed for both
populations, OCS populations exhibited these gains while
simultaneously retaining greater genetic variance and lower
inbreeding levels relative to TS populations
 Selection for wheat grain fructan content did not change plant height
but significantly decreased days to heading in OCS populations
 In this study, GS effectively improved the nutritional quality of wheat,
and OCS controlled the rate of inbreeding

30. Conclusion

31. Morrell et al., 2012
Genomic Selection Speeds Breeding

32. Thank you