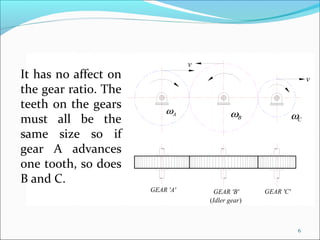
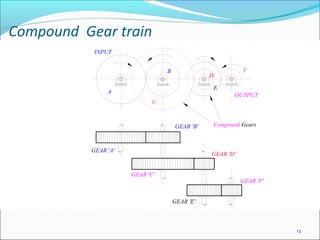
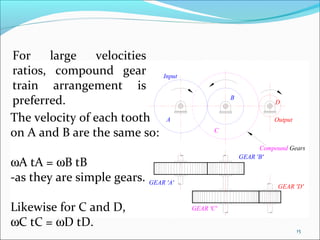
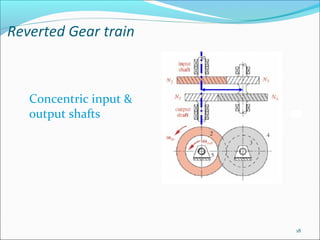
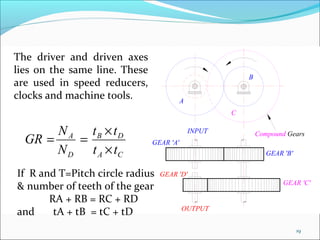
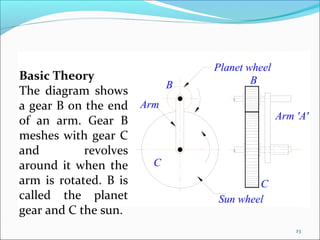
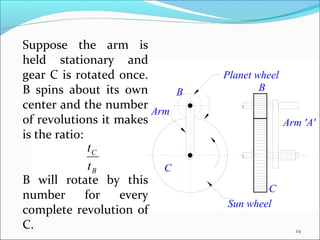
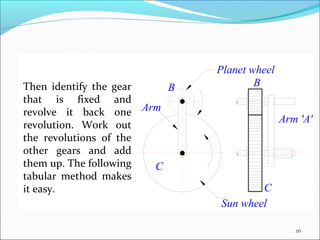
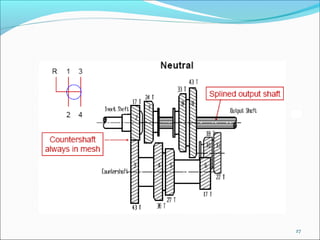
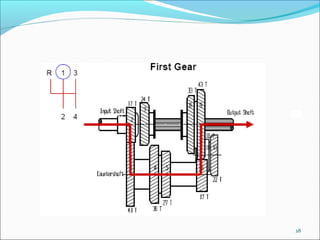
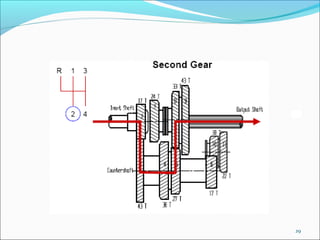
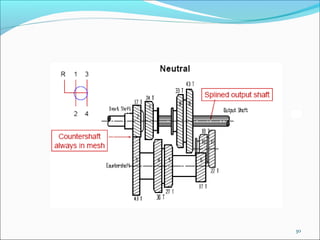
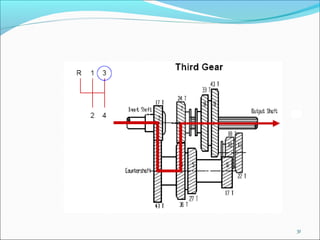
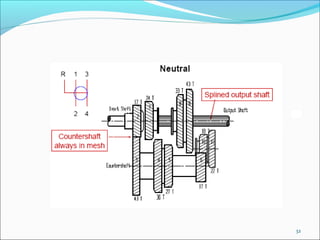
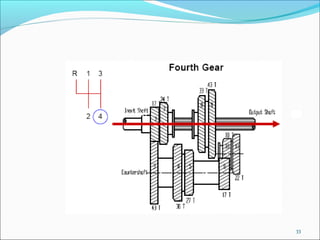
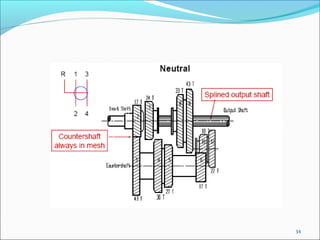
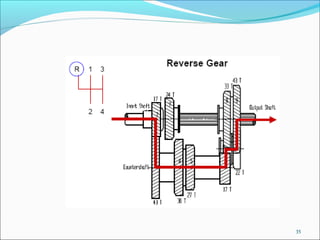
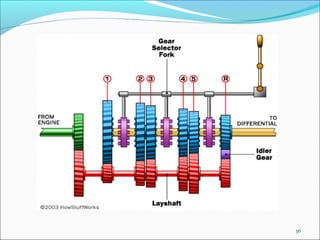
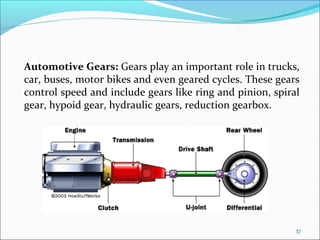
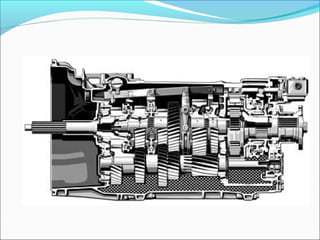
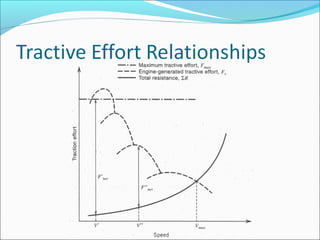
Gears play an important role in transmitting power in vehicles and machinery. They reduce speed and increase torque in gear trains and gear boxes. The document discusses different types of gears like spur gears, helical gears, bevel gears, and planetary (epicyclic) gears. It also explains how gears are used in automobiles, ships, wind turbines, power stations, mining equipment, and other applications to change rotational motion and speed. Resistance to vehicle motion from aerodynamic drag, rolling friction, and road grades must be overcome through the available tractive effort from the vehicle's engine and tires.

1. INTRODUCTION TO THE GEARS,
NEED FOR GEAR BOX AND
RESISTANCE TO VEHICLE MOTION

2. Gear Trains
A gear train is two or more gear working together
by meshing their teeth and turning each other in a
system to generate power and speed. It reduces
speed and increases torque. To create large gear
ratio, gears are connected together to form gear
trains. They often consist of multiple gears in the
train.
The most common of the gear train is the gear
pair connecting parallel shafts. The teeth of this
type can be spur, helical or herringbone. The
angular velocity is simply the reverse of the tooth
ratio.
2

3. Gear Trains
Any combination of gear
wheels employed to transmit
motion from one shaft to the
other is called a gear train.
The meshing of two gears
may be idealized as two
smooth discs with their
edges touching and no slip
between them. This ideal
diameter is called the Pitch
Circle Diameter (PCD) of
the gear.
3

4. Simple Gear Trains
4

5. Simple Gear Trains
The typical spur
v
gears as shown in
v
diagram. The
direction of rotation
ωA ωB
is reversed from one ωC
gear to another.
The only function of
the idler gear is to
change the direction GEAR 'A' GEAR 'B' GEAR 'C'
of rotation. (Idler gear)
5

6. v
It has no affect on v
the gear ratio. The
teeth on the gears ωA ωB ωC
must all be the
same size so if
gear A advances
one tooth, so does
B and C.
GEAR 'A' GEAR 'B' GEAR 'C'
(Idler gear)
6

7. t = number of teeth on the gear,
D = Pitch circle diameter, N = speed in rpm
D
m = module =
t
and
module must be the same for all
gears otherwise they would not mesh.
7

8. DA DB DC
m= = =
tA tB tC
DA = m t A; DB = m t B and DC = m t C
ω = angular velocity.
D
v = linear velocity on the circle. v = ω = ω r
2
The velocity v of any point on the circle must be the
same for all the gears, otherwise they would be slipping.
8

9. DA DB DC
v = ωA = ωB = ωC
2 2 2
ω A DA = ω B DB = ωC DC
ω A m t A = ω B m t B = ωC m t C
ω A t A = ω B t B = ωC t C
or in terms of rev / min
N A t A = N B t B = N C tC
9

10. DA DB DC
v = ωA = ωB = ωC
2 2 2
ω A DA = ω B DB = ωC DC
ω A m t A = ω B m t B = ωC m t C
ω A t A = ω B t B = ωC t C
or in terms of rev / min
N A t A = N B t B = N C tC
10

11. Input speed
The gear ratio is defined as GR =
Output speed
If gear A is the input and gear C is the output;
N A tC
GR = = also called as Speed ratio/Speed value
NC t A
N C Speed of driven gear
If = is called the Train value
N A Speed of driver gear
11

12. Simple Gear Trains
Application:
a) to connect gears where a large center distance is
required
b) to obtain desired direction of motion of the
driven gear ( CW or CCW)
c) to obtain high speed ratio
12

13. Compound Gear train
INPUT
B F
D
E
A
OUTPUT
C
GEAR 'B' Compound Gears
GEAR 'A'
GEAR 'D'
GEAR 'C'
GEAR 'F'
GEAR 'E'
13

14. Compound gears are
Input
simply a chain of simple
gear trains with the input B
D
of the second being the
output of the first. A chain A Output
of two pairs is shown C
below. Gear B is the output Compound Gears
of the first pair and gear C GEAR 'B'
is the input of the second
pair. Gears B and C are GEAR 'A'
GEAR 'D'
locked to the same shaft
and revolve at the same GEAR 'C'
speed.
14

15. For large velocities
ratios, compound gear Input
train arrangement is
preferred. B
D
The velocity of each tooth A Output
on A and B are the same so: C
Compound Gears
GEAR 'B'
ωA tA = ωB tB
-as they are simple gears. GEAR 'A'
GEAR 'D'
Likewise for C and D, GEAR 'C'
ωC tC = ωD tD.
15

16. ω A ωB ωC ω D
= and =
tB tA tD tC
tB × ωB tD × ωD
ωA = and ωC =
tA TC
tB × ωB tD × ωD
ω A × ωC = ×
tA tC
ω A × ωC t B t D
= ×
ω B × ω D t A tC
16

17. Compound Gear train
Since gear B and C are on the same shaft
Input
ω B = ωC
ω A tB tD B
D
= × = GR
ω D t A tC A Output
Since ω = 2 × π × N C
Compound Gears
The gear ratio may be GEAR 'B'
written as :
N ( In ) t B t D GEAR 'A'
GEAR 'D'
= × = GR
N ( Out ) t A tC GEAR 'C'
17

18. Reverted Gear train
Concentric input &
output shafts
18

19. The driver and driven axes
lies on the same line. These
B
are used in speed reducers,
clocks and machine tools. A
C
N A tB × tD INPUT
GR = =
Compound Gears
GEAR 'A'
N D t A × tC GEAR 'B'
If R and T=Pitch circle radius GEAR 'D'
GEAR 'C'
& number of teeth of the gear
RA + RB = RC + RD
OUTPUT
and tA + tB = tC + tD
19

20. Epicyclic Gear train
Epicyclic means one gear
revolving upon and around
another. The design
involves planet and sun
gears as one orbits the
other like a planet around
the sun. Here is a picture of
a typical gear box.
This design can produce large gear ratios in a small space and
are used on a wide range of applications from marine
gearboxes to electric screw drivers.
20

21. A small gear at
the center
called the sun,
several medium
sized gears
called the
planets and a
large external
gear called the
ring gear.
21

22. It is the system of epicyclic gears in which at least
one wheel axis itself revolves around another
fixed axis.
22

23. Planet wheel
Basic Theory B
B
The diagram shows
a gear B on the end Arm
of an arm. Gear B Arm 'A'
meshes with gear C
and revolves
around it when the C
arm is rotated. B is C
called the planet Sun wheel
gear and C the sun.
23

24. Suppose the arm is
held stationary and
gear C is rotated once. Planet wheel
B spins about its own B B
center and the number Arm
of revolutions it makes Arm 'A'
is the ratio:
tC
tB C
B will rotate by this
C
number for every
Sun wheel
complete revolution of
C. 24

25. Now consider the sun gear C
is restricted to rotate and the
arm A is revolved once. Gear
Planet wheel
B will revolve
B B
because of the orbit. It is this
extra rotation that causes Arm
confusion. One way to get Arm 'A'
round this is to imagine that
the whole system is revolved
once. C
C
tC Sun wheel
1+
tB
25

26. Planet wheel
Then identify the gear B B
that is fixed and
revolve it back one Arm
Arm 'A'
revolution. Work out
the revolutions of the
other gears and add
them up. The following C
tabular method makes
it easy. C
Sun wheel
26

27. 27

28. 28

29. 29

30. 30

31. 31

32. 32

33. 33

34. 34

35. 35

36. 36

37. Automotive Gears: Gears play an important role in trucks,
car, buses, motor bikes and even geared cycles. These gears
control speed and include gears like ring and pinion, spiral
gear, hypoid gear, hydraulic gears, reduction gearbox.
37

38. Depending on the size of
the vehicles, the size of the
gears also varies. There are
low gears covering a
shorter distance and are
useful when speed is low.
There are high gears also
with larger number of
teeth.
38

40. Conveyor Systems:
Conveyor is a mechanical
apparatus for carrying bulk
material from place to place
at a controlled rate; for
example an endless moving
belt or a chain of
receptacles. There are
various types of conveyors
that are used for different
material handling needs.

41. Agro Industry: All agro machinery consists of different
types of gears depending upon their function and
property. Different gears are used differently in the
industry.
Wind Turbine: When the rotor rotates, the load on the
main shaft is very heavy. It runs with approximate 22
revolutions per minute but generator has to go a lot faster.
It cannot use the turning force to increase the number of
revolutions and that is why wind turbine uses gear to
increase the speed.

42. Power Station:
Helical gears - Are used to
minimize noise and power losses.
Bevel gears - Used to change the
axis of rotational motion.
Spur gears - Passes power from
idler gears to the wheels.
Planetary gears - Used between
internal combustion engine and an
electric motor to transmit power.

43. Marine Gears: Marine gears meet a
wide variety of marine applications
in a variety of configurations and
installations to meet the most
critical applications.
Specific marine applications
include main propulsion,
centrifuges, deck machinery such
as winches, windlasses, cranes,
turning gears, pumps, elevators,
and rudder carriers.

44. Mining Gears: Mining is a process
of extracting ores or minerals from
the earth's surface. The gears are
used for increasing the torque
applied on the tool used for mining.
They are used for commercial gold
production, and coal mining.

45. Differential Gear Box

46. Throttle pedal , simply regulates the rate at which
the engine is doing work
At high speeds power output is high but torque
is low
Maximum torque may be available over only a
very limited speed range

47. One need to control power output and speed
range of the engine relative to range of speed over
which the vehicle is at any time likely to be
required to operate
A gear box is necessary , therefore , so that the
driver can regulate torque by selecting the
appropriate speed range or in other words , the
vehicle speed at which the maximum torque is
obtainable.

48. 1. Resistance
a. Aerodynamic
b. Rolling
c. Grade

49. Main Concepts
Resistance
Tractive effort
Vehicle acceleration
Braking
Stopping distance
F = ma + Ra + Rrl + Rg

50. Resistance is defined as the force impeding vehicle
motion
1. What is this force?
2. Aerodynamic resistance
3. Rolling resistance
4. Grade resistance
F = ma + Ra + Rrl + Rg

51. Aerodynamic Resistance Ra
Composed of:
1. Turbulent air flow around vehicle body (85%)
2. Friction of air over vehicle body (12%)
3. Vehicle component resistance, from radiators and air
vents (3%)
ρ
Ra = C D A f V 2
2
ρ
PRa = C D A f V 3
2
ft ⋅ lb
1 hp = 550
from National Research Council Canada sec

52. Rolling Resistance Rrl
Composed primarily of
1. Resistance from tire deformation (∼90%)
2. Tire penetration and surface compression (∼ 4%)
3. Tire slippage and air circulation around wheel (∼ 6%)
4. Wide range of factors affect total rolling resistance
5. Simplifying approximation:
Rrl = f rlW
 V 
PR rl = f rlWV f rl = 0.011 + 
ft ⋅ lb
 147 
1 hp = 550
sec

53. Grade Resistance Rg
Composed of
Gravitational force acting on the vehicle
Rg = W sin θ g θg
For small angles, sin θ g ≈ tan θ g
Rg = W tan θ g Rg
tan θ g = G
θg W
Rg = WG

54. Available Tractive Effort
The minimum of:
1. Force generated by the engine, Fe
2. Maximum value that is a function of the vehicle’s
weight distribution and road-tire interaction, Fmax
Available tractive effort = min ( Fe , Fmax )