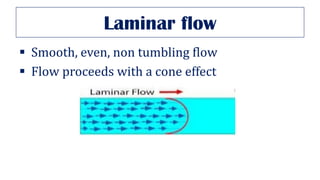
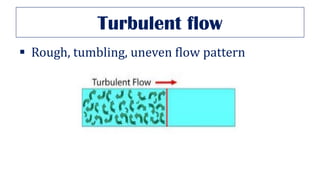
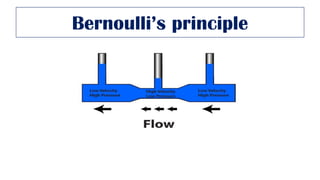
This document provides an overview of various gas laws and their applications in anesthesia. It discusses Boyle's, Charles', and Gay-Lussac's laws, as well as Avogadro's law, Dalton's law of partial pressures, the universal gas law, Hegan-Poissuilles law, Graham's laws of diffusion and effusion, Reynolds number, Bernoulli's principle, Venturi's effect, the Coanda effect, critical temperature, Poynting effect, Henry's law, and Raoult's law. Examples are given on how these principles apply to oxygen cylinders, nitrous oxide cylinders, gas flow and resistance, and the cost of inhalational agents.

1. DR TULSI RAM SHRESTHA, KMCTH

2. Contents
1. Boyles’s Law
2. Charle’s Law
3. Gay Lussac’s Law
4. Avagadro’s Law
5. Dalton’s Law
6. Universal gas law
7. Hegan-Poissuilles law
8. Graham’s law
9. Reynolds’s number
10. Graham’s law of diffusion
11. Bernoulli’s principle
12. Venturi’s effect
13. Coanda effect
14. Critical temperature
15. Poynting effect
16. Henry’s law
17. Raoult’s law

3. Boyle’s law
▪ At constant temperature (T), volume (V) of a
given mass of a gas is inversely proportional
to the absolute pressure(P)
V α 1/P
▪ PV= constant

4. Volume of oxygen in a full “E” type of cylinder
available for use at 15 psig (pressure at
common gas outlet)

5. ▪ Pressure in cylinder P1= 2000 psig
▪ Volume of the cylinder V1= 5L
▪ Volume of oxygen available( V2) at a pressure of P2 (15 psig)
▪ P1V1= P2V2
▪ 2000 X 5= 15 X V2
▪ V2=2000 x 5/15=665 litres
So, if we use 3L/min of oxygen, the E type full cylinder will last for about
220 mins

6. Charle’s law
▪ At constant pressure, volume of a gas is directly
proportional to the temperature.
V α T
▪ V/T= constant

7. Gay Lussac’s law
▪ At constant volume, pressure is directly
proportional to the temperature.
P α T
▪ P/T= constant

8. O2 cylinder shouldn't be kept under the sun
▪ P α T
▪ Pressure increases inside the cylinder
▪ Cylinder may even explode
▪ Hence the oxygen cylinders should be stored in
cool place.

9. Avogadro’s hypothesis
▪ Equal volume of gases contain equal number of
molecules(n) at STP.
▪ 1 mole of any gas at STP contain 6.023x10^23
molecules
▪ Occupies 22.4 litres of volume

10. N2O in E type cylinder
▪ cT: 36.5°C, RT-> liquid
▪ Wt of the liquid N2O (E): 3.3 kg
▪ Molecular weight of N2O is 14 × 2 + 16= 44
▪ So 44g of N2O will give 22.4 litres
▪ 3300 g will give (3300 X 22.4)/44= 1680L
▪ A full E type N2O cylinder will give 1680 L of
gas at STP

11. According to Charles's Law: V α T
▪ V1/T1=V2/T2
▪ 1680/273= V2/293
▪ V2=1803L
▪ Hence at room temperature, a full E type N2O
cylinder will give 1803 L of gas

12. Universal gas constant (R)
▪ PV = K1 (Boyle’s law)
▪ V/T = K2 (Charle’s law)
▪ P/T = K3 (Gay Lussac’s law)
▪ V=n
▪ PV/T=R
PV=nRT

13. Bourdon’s pressure gauge indicates
the content of oxygen cylinder
▪ PV= nRT
▪ P = n, i.e. pressure shown in the Bourdon’s gauge is
proportional to the number of molecules which is
the amount of gas in the cylinder.
▪ Hence the pressure gauge acts as a content gauge.
▪ If the gauge pressure in E type cylinder is showing
1000 PSI(half full), then the volume of gas one can
use-> 330L at 15 PSI.

14. Bourdon’s pressure gauge of N2O doesn’t
show the contents of cylinder
▪ N2O liquid at RT
▪ Doesn’t follow universal gas constant equation.
▪ Pressure in N2O Bourdon pressure gauge always shows
750 psig till all the liquid N2O becomes vapor.
▪ When all liquid N2O converts into the vapor, the Bourdon’s
pressure gauge will act as the content gauge
▪ And Boyle’s Law will be applicable.

15. Dalton’s law of partial pressure
▪ In a mixture of gases, pressure exerted by each
gas is same as the pressure exerted as if it
alone occupied the container.
▪ Total pressure exerted by mixture is equal to
sum of pressures exerted by individual gases.
▪ Partial pressure= fractional Conc. X total P

16. Hegan Poissuilles’ law
Q= Π r 4(P1 – P2)
8ƞL

17. Right sized ETT
▪ Laminar flow: Resistance increases by 4th power when
radius is decreased
▪ Any increase in R→ increase work of breathing→ early
fatigue of respiratory muscles
▪ Normal resistance offered by adult airway is < 2 cmH2O/
litre/sec
▪ Right sized ETT resistance increases to 5 cm H2O/ liter/sec
▪ Secretion in tube→ decrease lumen→resistance can
increase to 10 cm H2O/ liter/sec

18. Reynolds number
▪ Reynolds number = υρd/η
▪ >2000: turbulent flow

19. Laminar flow
▪ Smooth, even, non tumbling flow
▪ Flow proceeds with a cone effect

20. Turbulent flow
▪ Rough, tumbling, uneven flow pattern

21. Connectors with sharp curves
▪ At the sharp bends: turbulent flow
▪ Increase the resistance to the flow
▪ Wide bore & curved rather than sharp angles
preferred.

22. Graham’s law for turbulent flow

23. Heliox in a patient with tracheal stenosis
▪ Tracheal stenosis: turbulent gas flow→
increase in R, decrease flow
▪ Flow and R depend on the density of the gas as
per Graham’s law
▪ Mixture of O2 and helium→ decreased density
compared to O2 or air
▪ Hence Heliox→ decreased resistance,
increased flow

24. Flow meters
▪ Tapered glass tubes
▪ Lower part, flow of the gas is laminar
▪ Upper part, flow is turbulent
▪ Flow meters calibrated at 760 mm of Hg
▪ High altitude-> low atm P, density of the gas decreases
▪ Flow ά 1/√ density
▪ Flow will be higher than the actual flows that are set in the
flow meters

25. Bernoulli’s principle

26. ▪ In anesthesia machine: pressure regulation of
gases from cylinder to point of delivery to patient
▪ As gases from pressure regulators at a pressure of
45-60psig move towards flow meter assembly:
flow through flow restrictors (sudden narrowing
of the tubes)
▪ Here, pressure is further reduced but flow is
increased before reaching the flow meter assembly

27. Venturi effect
▪ Entrainment of air from the surrounding due to
fall in pressure at the point of constriction.

28. Pethik’s Test
▪ Expiratory valve and the inner tube closed
▪ 3 litres of flow of O2: reservoir bag is full
▪ O2 flush activated, thumb occluding the outer tube released
▪ If inner tube doesn’t have any leak
▪ then reservoir bag will collapse
▪ Venturi Effect
▪ At the opening of inner tube into the outer tube due to the
flow of 30-70 litres of O2 → sudden fall in the pressure,
sucking the O2 from the bag & collapsing it

29. Coanda effect
▪ Tendency of fluid jet to be attached
to a nearby surface
▪ If a constriction occurs at
bifurcation
▪ Increased in velocity
▪ Reduction of pressure
▪ Fluid/ air tends to stick to the side
of the branch→ maldistribution

30. Applications
▪ Unequal gas flow to alveoli where there has
been slight narrowing of bronchiole before it
divides
▪ Mucus plug at the branching of tracheo-
bronchial tree→ maldistribution of gases
▪ Unequal flow may result because of
atherosclerotic plaques in the vascular
tree→MI

31. Critical temperature
▪ Temperature above which the gas cannot be
compressed to its liquid state with any amount
of pressure
▪ Critical pressure is pressure of gas at its critical
temperature

32. Poynting effect
▪ When two gases, one of high and another of
low critical temperature→mixed in a
container
▪ The cT of the gas with high cT will decrease
to a lower level (pseudo cT) and the mixture
will remain as a gas above this pseudo cT

33. Entonox in very cold climate
▪ Entonox-> 50:50 mixture of O2 & N2O
▪ The cT of O2: -118°C and of N2O is 37°C
▪ When these gases are mixed in a same cylinder, then cT of the mixture:
- 6°C due to Poynting Effect
▪ Mixture will remain as gas at RT.
▪ In cold climates (T< -6°C), then N2O separates into its liquid form and
remain at bottom of the cylinder: the patient will get only O2 initially
and hence will not produce any analgesia.
▪ Later patient gets only N2O which can result in hypoxia.
▪ Hence the cylinder should be thoroughly shaken before use.

34. Adiabatic change
▪ When a gas is subjected to sudden
compression, heat energy is produced
▪ Reverse occurs with sudden expansion
▪ No exchange of energy with surroundings

35. Why open O2 cylinder slowly
▪ Rapid opening of the valve
▪ Rapid flow of oxygen
▪ Rapid compression of oxygen in narrow
tube
▪ Very high temperature leading to possible
explosion

36. Joule thompson effect
▪ When gas is allowed to escape through a
narrow opening-> sudden temperature drop
▪ Used in manufacture of oxygen from air

37. ▪ Air is compressed suddenly-> gets heated up
▪ Cooled by external cooling and made to suddenly expand->
loses further temperature as energy is spent in order to
hold the molecules together (Vander Waal force)
▪ Repeated many times→ temp reduces to <-183C
▪ Through fractional distillation, liquid O2 collected in the
lower part is separated from nitrogen (collects at the top of
the container)

38. Henry’s law
▪ Amount of a gas dissolved in a unit volume of a
solvent is directly proportional to its partial
pressure at STP
▪ Predicts how much of a gas dissolves in a liquid
▪ V = α x PGAS
▪ V = volume of the gas dissolved, α solubility
coefficient of the gas in the liquid and Pgas is the
partial pressure above the liquid

39. ▪ Amount of gas carried in solution in blood
▪ Solubility coefficient of oxygen is 0.003 ml/dl
▪ At 100mmHg of oxygen tension , the amount of
oxygen in the dissolved form will be 0.3 ml.

40. Raoult’s law
▪ Reduction of vapour pressure of a solvent is
proportional to molar concentration of the
solute.
▪ Raoult’s law is applied for azeotropes

41. ▪ Azeotrope is a mixture which vaporizes in the
same proportion as the volume concentrations
of the components in solution
▪ Ether and halothane form an azeotrope,
provided that they are in the ratio of 1:2

42. ▪ Molar concentration of ether is 3.19mol/litre and
halothane is 6.30 mols/litre
▪ According to Raoult’s law the vapour pressure will
also be in the same proportions
▪ Components of azeotrope evaporate in the ratio of
one part of ether to two parts of halothane
▪ Relative volume concentration of the liquid
mixture do not change.

43. Cost of Inhalational agent
▪ 1ml of liquid sevoflurane will give 180 ml of vapour
▪ If 2% of sevoflurane is used with a fresh gas flow of 6 litres
▪ Every minute 120 ml of vapour will be used
▪ Per hour it will be 7200ml of vapour
▪ Since 1ml of liquid sevoflurane will give 180 ml of vapour,
then 7200/180=40 ml of the liquid sevoflurane will be
used per hour
▪ Cost of 250 ml of sevoflurane is Rs. 7500
▪ 40 ml would cost 7500/40x30=Rs 1200