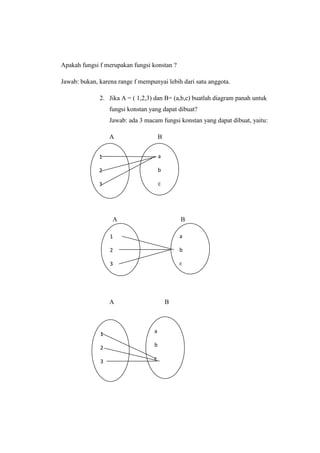
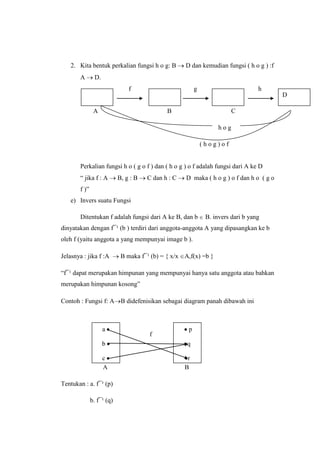
Dokumen tersebut membahas tentang produk cartesius, relasi, dan fungsi. Produk cartesius adalah himpunan semua pasangan terurut yang terdiri dari elemen-elemen dari dua himpunan. Relasi adalah subset dari produk cartesius dua himpunan yang mendefinisikan hubungan antara elemen-elemennya. Ada berbagai jenis relasi seperti relasi refleksif, simetris, transitif. Fungsi adalah relasi khusus antara dua himp