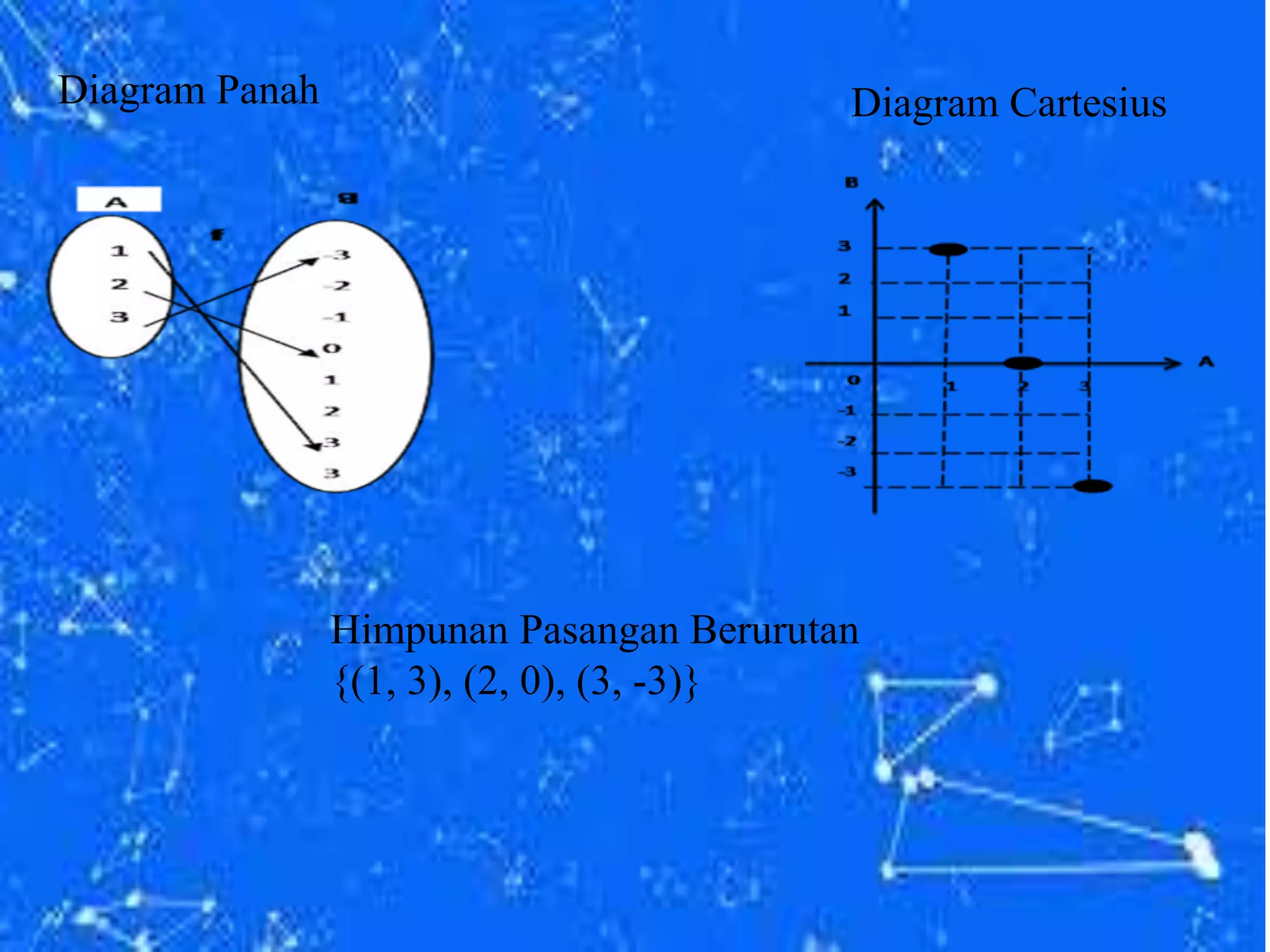
Relasi dan fungsi merupakan konsep penting dalam matematika. Relasi adalah hubungan antara dua elemen atau himpunan, sedangkan fungsi adalah relasi khusus dimana setiap elemen domain dipetakan ke tepat satu elemen kodomain. Dokumen ini menjelaskan pengertian, sifat, dan jenis-jenis relasi dan fungsi beserta contoh-contoh penerapannya.

1. RELASI DAN FUNGSI
Disusun oleh kelompok 10:
Nadia(190141607)
Ratna kusari(190141621)
Sista Anggini Saputri(190141635)
DOSEN pengampuh: Putri Cahyani
Agustine M.Pd

2. Pengertian Relasi
Relasi adalah hubungan antara dua elemen atau
dua himpunan. Relasi juga dikatakan sebagai
suatu aturan yang memasangkan anggota
himpunan satu ke himpunan lain.

3. Metode-metode menyatakan relasi
1. Dengan himpunan pasangan berurutan
Himpunan yang anggotanya semua pasangan
berurutan (x,y) dinamakan himpunan pasangan berurutan.
{(Tias, Voli), (Jamal, Voli), (Jamal, Basket), (Farid, Voli),
(Farid, Basket), (Farid, Tenis), (Dika, Tenis)}.
2. Dengan Diagram Panah
3. Dengan Diagram Cartesius

4. Sifat-sifat relasi
 Relasi Refleksif ( Bercermin)
 Jika diketahui A= {1,2,3,4} dan relasi R= {(1,1), (2,2), (3,3), (4,4)} Pada A, maka R x∈A
adalah refleksif, karena untuk setiap x∈A terdapat (x,x) pada R.
Perhatikan relasi pada himpunan = {1,2,3,4} berikut:
 R1= {(1,1), (1,2), (1,4), (2,1), (2,2), (3,3), (4,1), (4,4)}
 R2= {(1,1), (1,2), (1,3), (1,4), (2,2), (2,3), (2,4), (3,3), (3,4), (4,4)}
 Relasi-relasi tersebut merupakan relasi refleksif karena memiliki elemen (1,1), (2,2), (3,3),
dan (4,4).
 Relasi Irrefleksif
 Diketahui :
 himpunan B= {a,b,c} dan relasi R= {(a,c), (b,c), (b,a)}.
 Relasi R adalah irrefleksif, karena (a,a), (b,b), dan (c,c) bukan elemen.
 Diketahui :
 A= {1,2,3,4} dan relasi R= {(2,1), (3,2), (4,1), (4,2), (4,3)}.
 Relasi R merupakan relasi irrefleksif, karena tidak terdapat elemen (x,x), dimana x∈A.
 Relasi Nonrefleksif
 Perhatikan relasi pada himpunan A= {1,2,3,}
 R= {(1,1), (1,2), (2,2), (2,3), (3,3)}
 Relasi tersebut merupakan relasi non refleksif, karena ada (1,2) dan (2,3).

5.  Relasi Simetri
 Relasi R = { (a,b), (b,a), (a,c), (c,a) } dalam himpunan {a, b, c}.
 Ani menyukai Budi, Budi menyukai Ani {(Ani,Budi),(Budi,Ani)}
 Relasi Asimetri
 Relasi R = { (a,b), (b,c), (c,a) } dalam himpunan { a,b,c }.
 Relasi Nonsimetri
Relasi R = { (a,b), (a,c), (c,a) } dalam himpunan {a, b, c}
 Relasi Antisimetri
 A = keluarga himpunan. Relasi “ himpunan bagian” adalah relasi
yang antisimetris pada A, karena untuk setiap dua himpunan x dan y,
jika x y dan y x, maka x = y.
 Relasi Transitif
 Relasi R = {(a,b), (b,c), (a,c), (c,c) } dalam himpunan { a,b,c }.
 Relasi Nontransitif
 R = {(1,2),(2,3),(3,4)} dalam himpunan { 1,2,3,4}
 Relasi Intransitif

6. Komposisi Relasi
Misalkan :
R adalah relasi dari himpunan A ke himpunan B
T adalah relasi dari himpunan B ke himpunan C.
Komposisi R dan S, dinotasikan dengan T ο R, adalah relasi
dari A ke C yang didefinisikan oleh :
T ο R = {(a, c) | a ∈ A, c ∈ C, dan untuk suatu b ∈ B sehingga
(a, b) ∈ R dan (b, c) ∈ S }

7. Fungsi
Pengertianfungsi
Fungsi dari himpunan A ke himpunan B adalah
relasi yang memasangkan setiap anggota
himpunan A(daerah asal atau domain), dengan
tepat satu anggota himpunan B(daerah kawan
atau kodomain). Himpuan nilai yang diperoleh
disebut daerah hasil (range).
Domain, Kodomain, Dan Range
f : A → B
A dinamakan daerah asal (domain)
dari f dan B dinamakan daerah hasil
(Kodomain) dari f.
Misalkan f(a) = b,
maka b dinamakan bayangan (image)
dari a,
dan a dinamakan pra-bayangan (pre-
image) dari b.
Himpunan yang berisi semua nilai
pemetaan f dinamakan jelajah (range)
dari f.

8. Penulisan Fungsi
a. Himpunan pasangan terurut.
Misalkan fungsi kuadrat pada himpunan {1, 2, 3, 4, 5,
6, 7, 8, 9,10} maka fungsi itu dapat dituliskan dalam
bentuk :
f = {(2, 4), (3, 9)}
b. Formula pengisian nilai (assignment)
f(x) = x2 + 10,
f(x) = 5x

9. Sifat-sifat Fungsi
a. Fungsi injektif (satu-satu)
b. Fungsi surjektif (onto)
c. Fungsi bijektif (korespondensi satu-satu)

10. Jenis-jenis Fungsi
1. Fungsi konstan (fungsi tetap)
Suatu fungsi f : A → B ditentukan dengan rumus f(x) disebut fungsi konstan
apabila untuk setiap anggota domain fungsi selalu berlaku f(x) = C, di mana C bilangan
konstan.
2. Fungsi linear
Suatu fungsi f(x) disebut fungsi linear apabila fungsi itu ditentukan oleh f(x) =
ax + b, di mana a ≠ 0, a dan b bilangan konstan dan grafiknya berupa garis lurus.
3. Fungsi Kuadrat
Suatu fungsi f(x) disebut fungsi kuadrat apabila fungsi itu ditentukan oleh f(x)
= ax2 + bx + c, di mana a ≠ 0 dan a, b, dan c bilangan konstan dan grafiknya berupa
parabola.
4. Fungsi identitas
Suatu fungsi f(x) disebut fungsi identitas apabila setiap anggota domain fungsi
berlaku f(x) = x atau setiap anggota domain fungsi dipetakan pada dirinya sendiri.

11. Menyatakan Fungsi
contoh :
Misalkan A = {1, 2, 3} dan B = {-3, -2, -1, 0, 1, 2}.
Jika fungsi f : A → B ditentukan dengan f(x) = 6 - 3x.
Nyatakan dalam diagram panah, diagram cartesius, dan
pasangan berurutan
Penyelesaian :
f(1) = 6 – 3 (1) = 6 – 3= 3
f(2) = 6 – 3(2) = 6 – 6 = 0
f(3) = 6 – 3(3) = 6 – 9 = -3

12. Diagram Panah Diagram Cartesius
Himpunan Pasangan Berurutan
{(1, 3), (2, 0), (3, -3)}

13. SEKIAN
DAN
TERIMAKASIH