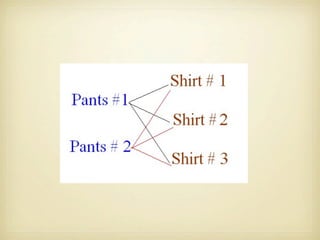
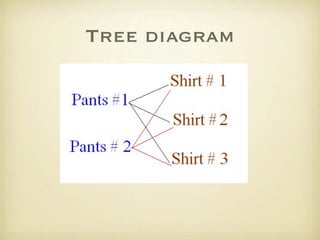
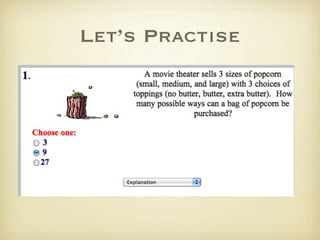
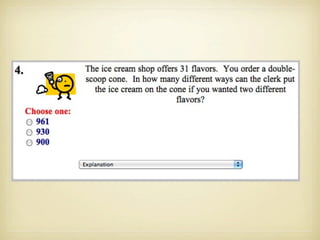
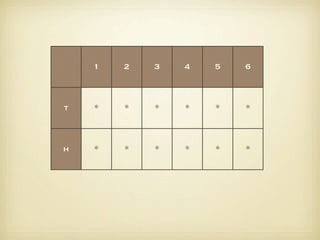
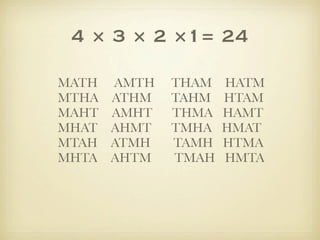The document discusses counting principles and permutations. It introduces the fundamental principle of counting, which states that if one event has m possible outcomes and a second event has n possible outcomes, the total number of outcomes when performing both events is m × n. It also discusses permutations and factorial notation. Examples are provided to demonstrate counting the number of possible arrangements and outcomes in different scenarios.

1. Bobbi-Bear
Ms. Carter

2. Bobbi Bear
• http://illuminations.nctm.org/activitydetail.aspx?id=3

4. Tree diagram

5. • When dealing with the occurrence of more
than one event or activity, it is important to
be able to quickly determine how many
possible outcomes exist.
• For example, if ice cream sundaes come in 5
flavors with 4 possible toppings, how many
different sundaes can be made with one
flavor of ice cream and one topping?

6. • When dealing with the occurrence of more
than one event or activity, it is important to
be able to quickly determine how many
possible outcomes exist.
• For example, if ice cream sundaes come in 5
flavors with 4 possible toppings, how many
different sundaes can be made with one
flavor of ice cream and one topping?
Guesses??

7. • When dealing with the occurrence of more
than one event or activity, it is important to
be able to quickly determine how many
possible outcomes exist.
• For example, if ice cream sundaes come in 5
flavors with 4 possible toppings, how many
different sundaes can be made with one
flavor of ice cream and one topping?
Guesses??
20!!!

8. Introduce..

9. Introduce..
The Fundamental
Principle of
Counting

10. Operations
• The result of an operation is an outcome.
For example, if we throw a die, one
possible outcome is 5.
If we throw a die there are six possible
outcomes: 1, 2, 3, 4, 5 or 6.

11. Suppose one operation has m possible
outcomes and that a second operation has n
outcomes. The number of possible outcomes
when preforming the first operation followed
by the second operation is m × n.
Performing one operation and another
operation means we multiply the number of
possible outcomes.
m×n

12. Example
Activity:
draw two cards from a standard deck of 52
cards without replacing the cards
There are 52 ways to draw the first card.
There are 51 ways to draw the second card.
There are 52 • 51 = 2,652 ways to draw the
two cards.

13. • Suppose one operation has m possible outcomes
and that a second operation has n outcomes.
The number of possible outcomes when
preforming the first operation or the second
operation is m + n.
Performing one operation or another operation
means we add the number of possible outcomes.
m+n
NOTE: We assume it is not possible for both operations to occur. In other words,
there is no overlap of the two operations.

14. Let’s Practise

18. Last One!

19. Permutations
it is an arrangement of a number of
objects in a definite order.

20. Example
• How many ways are there of arranging all the
letters of the word MATH?

21. 4 × 3 × 2 ×1= 24
MATH AMTH THAM HATM
MTHA ATHM TAHM HTAM
MAHT AMHT THMA HAMT
MHAT AHMT TMHA HMAT
MTAH ATMH TAMH HTMA
MHTA AHTM TMAH HMTA

22. Example 1
• If a die is thrown and a coin is tossed, how many
different outcomes are possible?
• Write out all of the outcomes.

23. Solution
• Represent each operation with an empty box: Die × Coin
×
1. There are six possible outcomes for a die:
1, 2, 3, 4, ,5 or 6.
2. There are two possible outcomes for a
coin: H or T.
Hence, the no. of different outcomes
= 6 × 2 =12

24. 1 2 3 4 5 6
t * * * * * *
h * * * * * *

25. Example 2
• In a cinema, a customer in the VIP section
has three choices of snacks: popcorn,
nachos or candyfloss. The customer also
has three choices of drink: water, cola or
wine.
(i) Write down all the different selections possible.
(ii) How many different selections are possible?
(iii) If your class went on a school trip to that VIP
cinema, which selection(s) in your opinion would
be (a) most popular (b) least popular?
Justify your answer.

26. Solution
• (i) The possible answers are:
Nachos and Wine Popcorn and Wine Candyfloss and Wine
Nachos and Cola Popcorn and Cola Candyfloss and Cola
Nachos and Water Popcorn and Water Candyfloss and Water
WE CALL SUCH A LIST, WITH ALL POSSIBLE
OUTCOMES, THE SAMPLE SPACE.

27. • (ii) Using the fundamental principle of
counting
Choices for Snack × Choices for Drink
3 × 3 =9
Alternative Method: Two-Way Table
Wine Cola Water
Nachos
Popcorn
Candyfloss

28. (iii)
• In a justify/discuss type of question, there are no
correct or incorrect answers. If you can back up
your opinion with a logical statement, you are
answering the question correctly.

29. Factorials

30. The product of all the positive whole numbers
from n down to 1 is called factorial n and is
denoted by n!
Thus n! = n(n-1)(n-2).. × 3 ×2 ×1.

31. Text

32. Working with
Factorials
Let’s Try Dividing!

33. Example

34. Example
Divide 20! by 10!

35. Example
Divide 20! by 10!

36. Example
Divide 20! by 10!
Expand the factorials.

37. Example
Divide 20! by 10!
Expand the factorials.

38. Example
Divide 20! by 10!
Expand the factorials.
Multiply and Answer:

39. Example
Divide 20! by 10!
Expand the factorials.
Multiply and Answer:

40. Example 2
A student has five reference books, one each on
Maths, Geography, Art, history and Economics.
The books are to be placed in a row on the shelf.
Question 1
How many arrangements are possible?

41. Example 2
A student has five reference books, one each on
Maths, Geography, Art, history and Economics.
The books are to be placed in a row on the shelf.
Question 1
How many arrangements are possible?

42. Example 2
A student has five reference books, one each on
Maths, Geography, Art, history and Economics.
The books are to be placed in a row on the shelf.
Question 1
How many arrangements are possible?
Shelf

43. Example 2
A student has five reference books, one each on
Maths, Geography, Art, history and Economics.
The books are to be placed in a row on the shelf.
Question 1
How many arrangements are possible?
Shelf

44. Example 2
A student has five reference books, one each on
Maths, Geography, Art, history and Economics.
The books are to be placed in a row on the shelf.
Question 1
How many arrangements are possible?
Shelf

45. Example 2
A student has five reference books, one each on
Maths, Geography, Art, history and Economics.
The books are to be placed in a row on the shelf.
Question 1
How many arrangements are possible?
Shelf

46. Example 2
A student has five reference books, one each on
Maths, Geography, Art, history and Economics.
The books are to be placed in a row on the shelf.
Question 1
How many arrangements are possible?
Shelf

47. Example 2
A student has five reference books, one each on
Maths, Geography, Art, history and Economics.
The books are to be placed in a row on the shelf.
Question 1
How many arrangements are possible?
Shelf

48. Example 2
A student has five reference books, one each on
Maths, Geography, Art, history and Economics.
The books are to be placed in a row on the shelf.
Question 1
How many arrangements are possible?
Shelf
5 choices 4 choices 3 choices 2 choices 1 choices

49. Example 2
A student has five reference books, one each on
Maths, Geography, Art, history and Economics.
The books are to be placed in a row on the shelf.
Question 1
How many arrangements are possible?
Shelf
5 choices 4 choices 3 choices 2 choices 1 choices
5 × 4 × 3 × 2 × 1 = 120