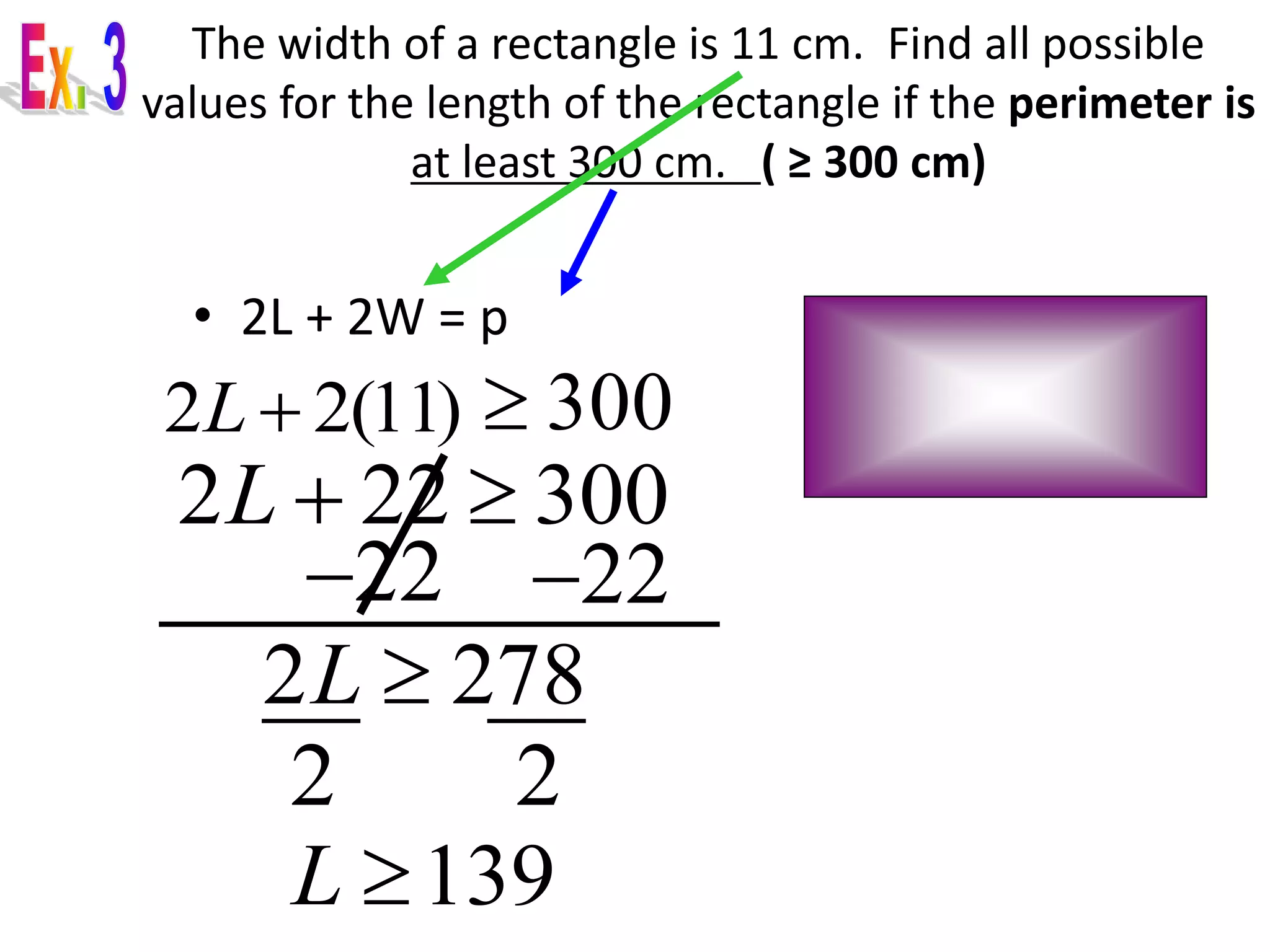
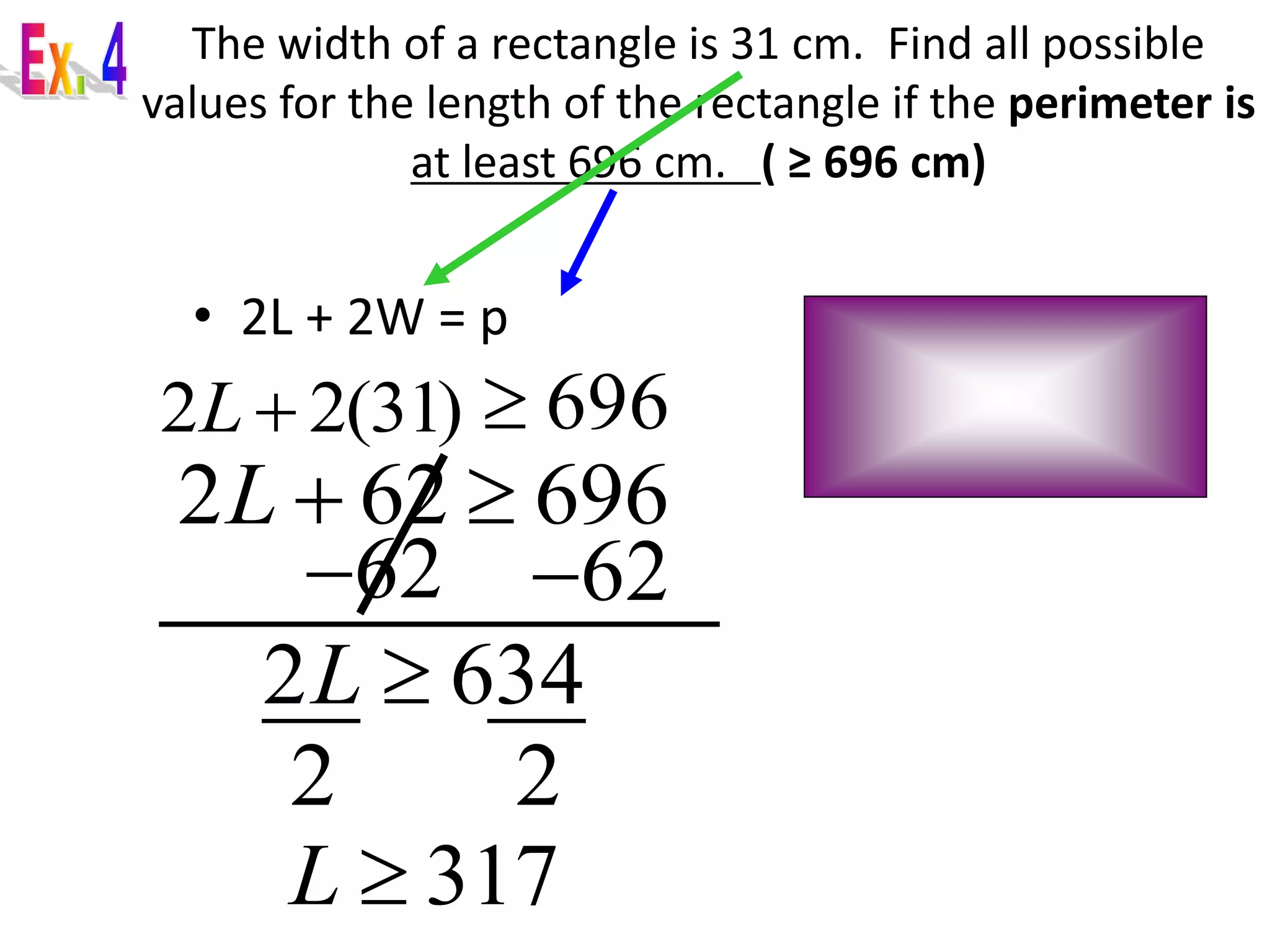
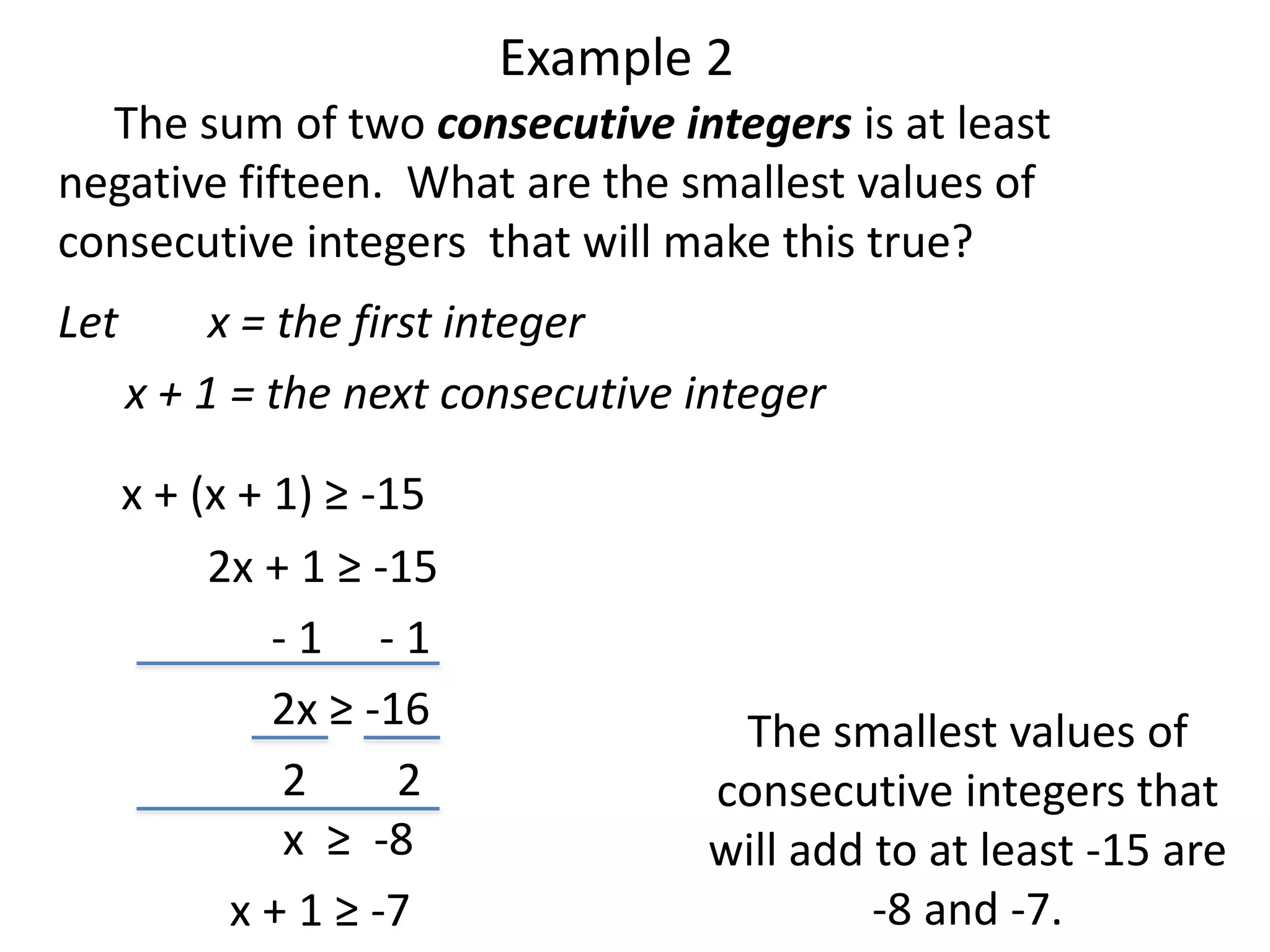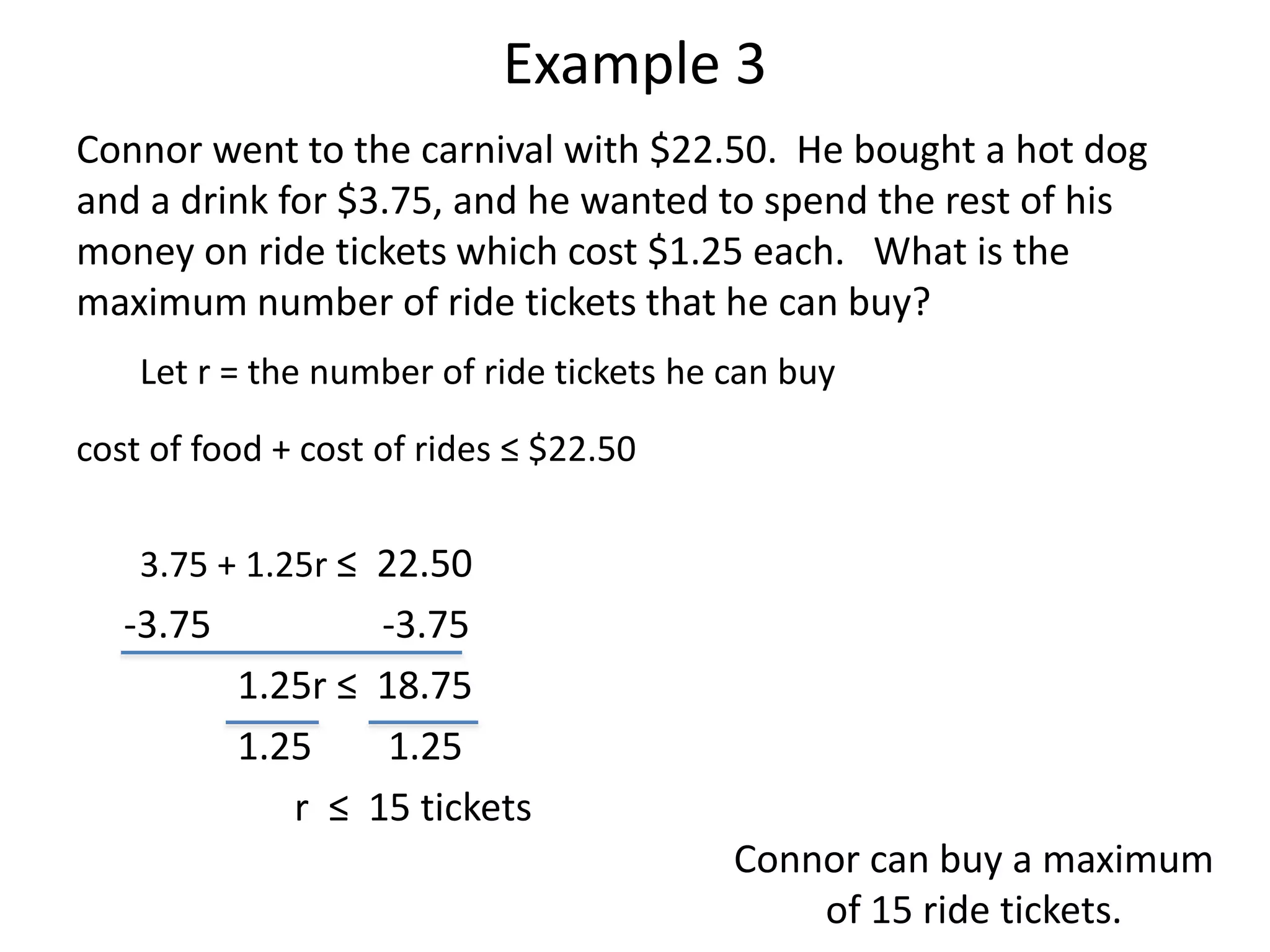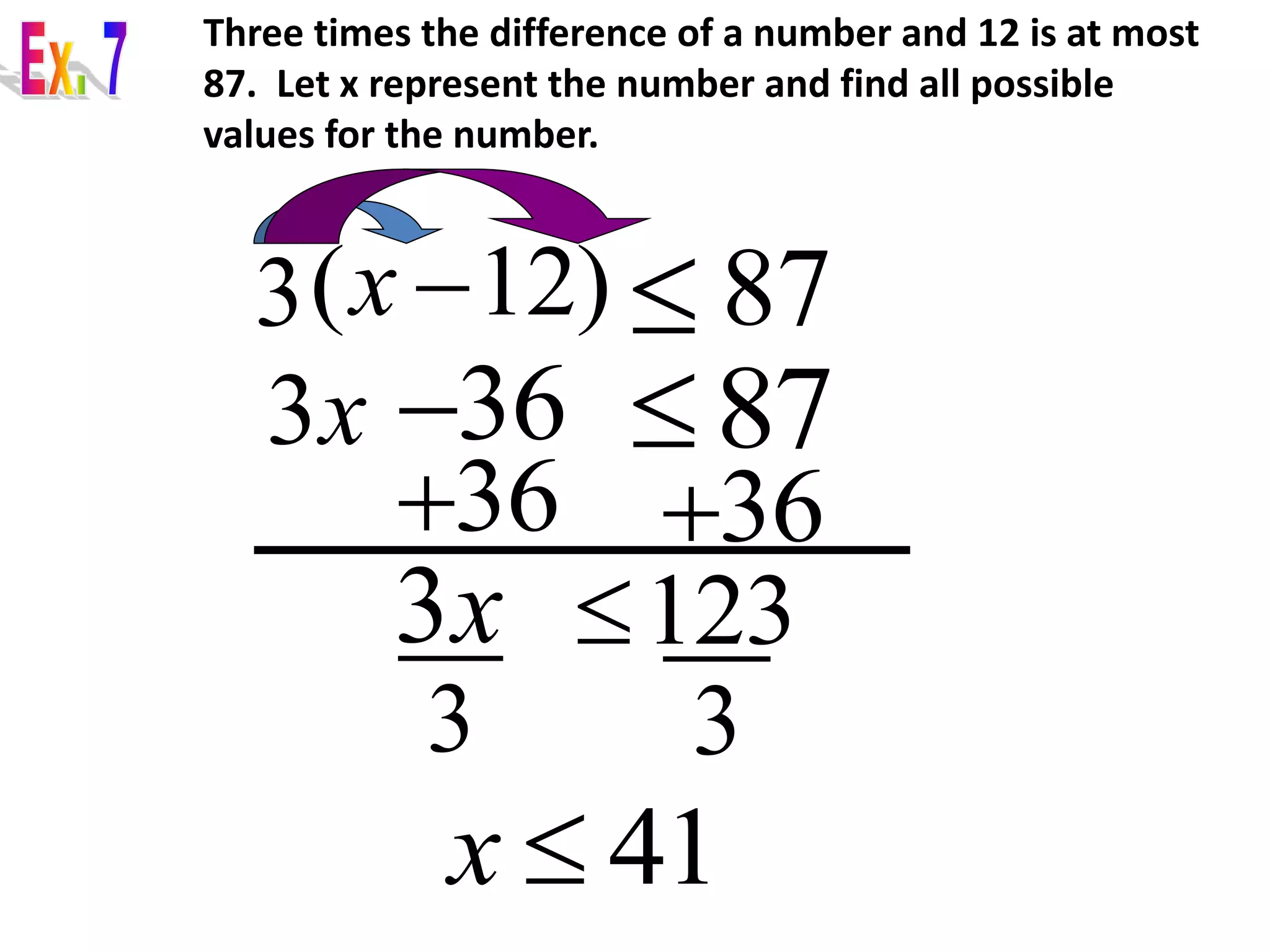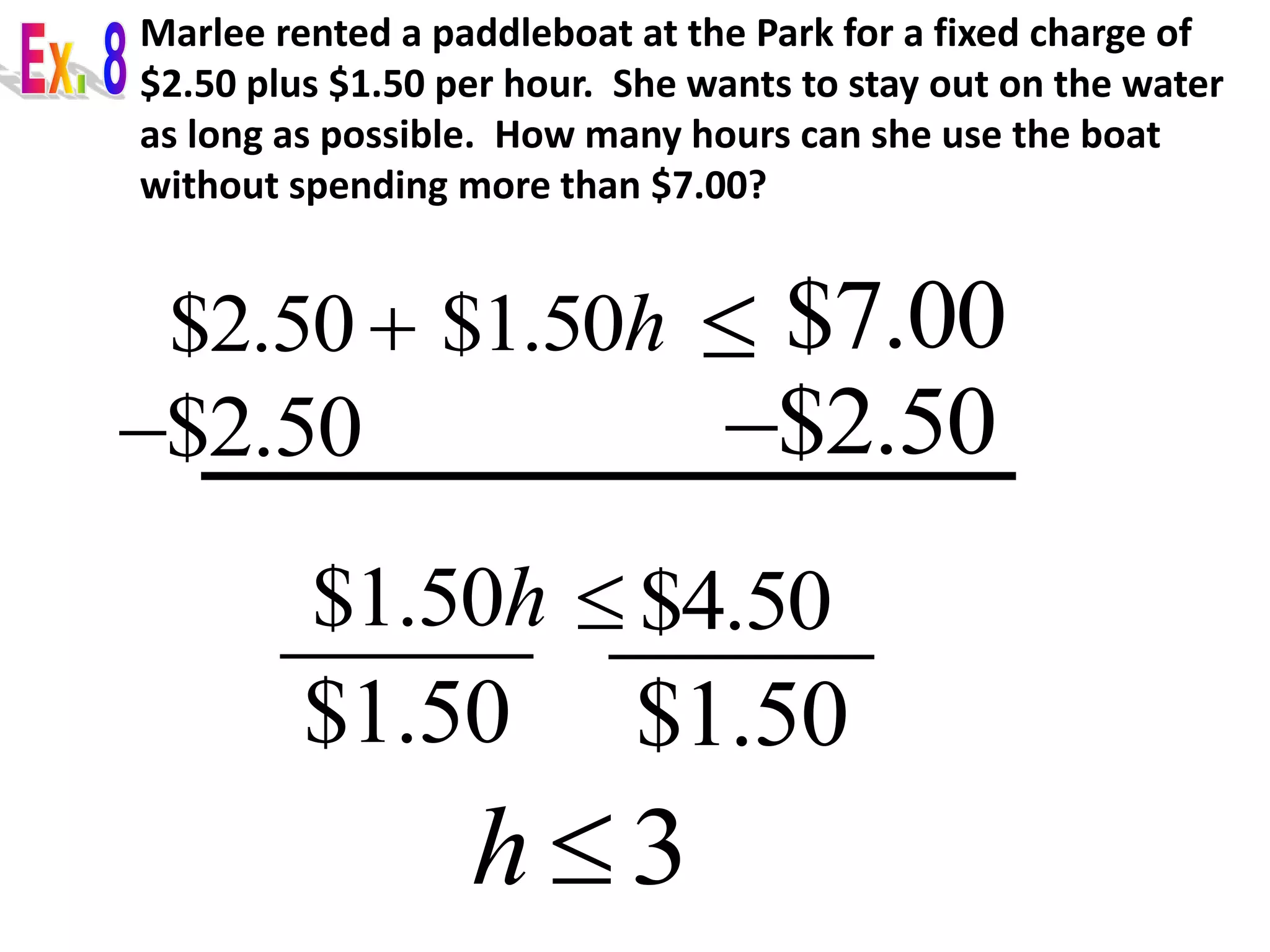The document provides examples of word problems involving inequalities. It gives steps to follow, such as defining variables, writing inequalities, solving, and checking answers. Several examples are worked through, applying these steps to problems about numbers, rates, areas, and time. The examples demonstrate how to set up and solve linear inequalities to find possible values that satisfy the given relationships.

1. Word Problems
with Inequalities
Don’t panic! Remember to:
• Read the questions carefully.
• Define the variable.
• Write an inequality.
• Solve the inequality.
• Check that your answer is reasonable.
• Answer in a complete sentence.

2. Keywords for Inequalities

3. Example 1
Eight less than the product of -3 and a number is
greater than -26. Write and solve an inequality to
represent this relationship. Graph the solution set, and
check your answer.
Let x = the number
-3x – 8 > -26
+8 +8
-3x > -18
-3 -3
x < 6
4 5 6 7 8
CHECK @ x = 5
-3x – 8 > -26
-3(5) – 8 > -26
-15 – 8 > -26
Don’t forget to reverse the inequality sign -23 > -26
when dividing by a negative!

4. Example 2
The sum of two consecutive integers is at least
negative fifteen. What are the smallest values of
consecutive integers that will make this true?
Let x = the first integer
x + 1 = the next consecutive integer
x + (x + 1) ≥ -15
2x + 1 ≥ -15
- 1 - 1
2x ≥ -16
2 2
x ≥ -8
x + 1 ≥ -7
The smallest values of
consecutive integers that
will add to at least -15 are
-8 and -7.

5. Example 3
Connor went to the carnival with $22.50. He bought a hot dog
and a drink for $3.75, and he wanted to spend the rest of his
money on ride tickets which cost $1.25 each. What is the
maximum number of ride tickets that he can buy?
Let r = the number of ride tickets he can buy
cost of food + cost of rides ≤ $22.50
3.75 + 1.25r ≤ 22.50
-3.75 -3.75
1.25r ≤ 18.75
1.25 1.25
r ≤ 15 tickets
Connor can buy a maximum
of 15 ride tickets.

6. Example 4
Stan earned $7.55 per hour plus an additional $100 in
tips waiting tables on Saturday evening. He earned
$160 in all. To the nearest hour, what is the least
number of hours Stan would have to work to earn this
much money?
Let h = the number of hours Stan will have to work
tips + hourly wages ≥ $160
100 + 7.55h ≥ 160
-100 -100
7.55h ≥ 60
7.55 7.55
x ≥ 7.9 hours
To the nearest hour, Stan
would have to work at
least 8 hours to earn $160.

7. Example 5
Brenda has $500 in her bank account. Every week, she
withdraws $40 for expenses. Without making any
deposits, how many weeks can she withdraw this money
if she wants to maintain a balance of at least $200?
Let w = the number of weeks Brenda withdraws money
starting account balance – money withdrawn ≥ $200
500 – 40w ≥ 200
-500 -500
– 40w ≥ -300
– 40 – 40
w ≤ 7.5 weeks
Don’t forget to reverse the inequality
sign when dividing by a negative!
Brenda can withdraw $40
from the account for 7 full
weeks and still have at
least $200 in the account.

8. Sean earns $6.70 per hour working after school. He needs
at least $155 (≥ 155) for a stereo system. Write an
inequality that describes how many hours he must work to
reach his goal.
$6.70 h ≥ 155
Per means to multiply
To figure your pay check:
You multiply rate times hours worked
$6.70 $6.70
h  23.1343
So 23 hours
is not enough
So Sean must
Work 24 hours
To earn enough
Money.
h  24

9. Sean earns $6.85 per hour working after school. He needs
at least $310 (≥ 310) for a stereo system. Write an
inequality that describes how many hours he must work to
reach his goal.
$6.85 h ≥ 310
Per means to multiply
To figure your pay check:
You multiply rate times hours worked
$6.85 $6.85
h  45.25547
So 45 hours
is not enough
So Sean must
Work 46 hours
To earn enough
Money.
h  46

10. The width of a rectangle is 11 cm. Find all possible
values for the length of the rectangle if the perimeter is
at least 300 cm. ( ≥ 300 cm)
• 2L + 2W = p
2L  2(11)  300
2L  22  300
22 22
2L  278
2 2
L 139

11. The width of a rectangle is 31 cm. Find all possible
values for the length of the rectangle if the perimeter is
at least 696 cm. ( ≥ 696 cm)
• 2L + 2W = p
2 2(31) L  696
2L  62  696
62 62
2L  634
2 2
L  317

12. The perimeter of a square is to be between 11 and 76 feet,
inclusively. Find all possible values for the length of its sides.
• 4 equal sides
• Perimeter – add up
sides s
s s
s
P = s +s+s+s=4s
11 p  76
11 4s  76
4 4 4
2.75  s 19

13. The perimeter of a square is to be between 14 and 72 feet,
inclusively. Find all possible values for the length of its sides.
• 4 equal sides
• Perimeter – add up
sides s
s s
s
P = s +s+s+s=4s
14  p  72
14  4s  72
4 4 4
3.5  s 18

14. Three times the difference of a number and 12 is at most
87. Let x represent the number and find all possible
values for the number.
3( 12) x  87
3x 36 87 
36 36
3x 123 
3 3
x  41

15. Marlee rented a paddleboat at the Park for a fixed charge of
$2.50 plus $1.50 per hour. She wants to stay out on the water
as long as possible. How many hours can she use the boat
without spending more than $7.00?
$2.50 $1.50h  $7.00
$2.50  $2.50 
$1.50h  $4.50
$1.50 $1.50
h  3