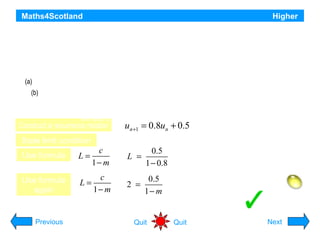
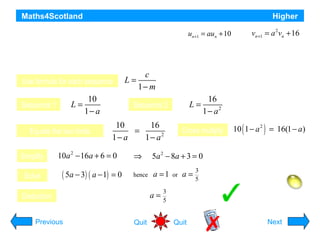
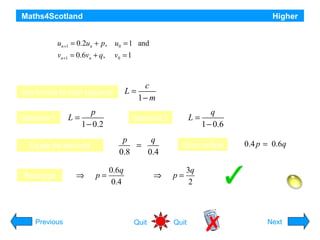
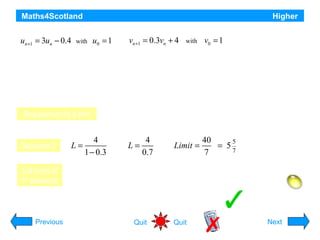
This document provides information about recurrence relations and their applications in higher mathematics. It begins by introducing different types of sequences and exploring whether they can be described by a formula or recurrence relation. It then discusses linear recurrence relations and how they can model growth and decay scenarios. The document also covers divergence and convergence of sequences, and provides examples of applying recurrence relations to problems involving populations, waste disposal, medication in hospitals, and other scenarios.