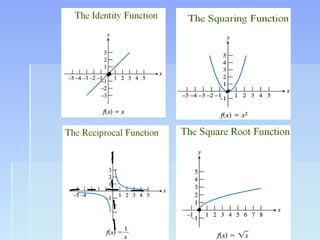
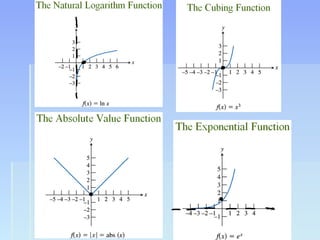
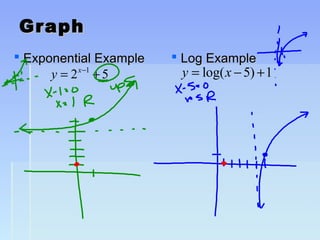
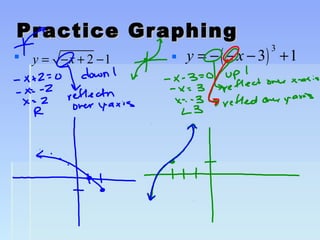
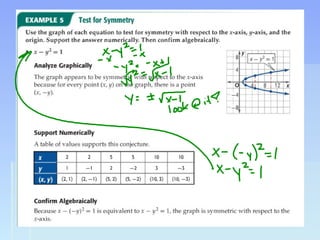
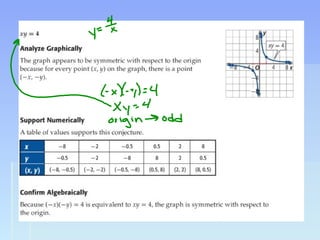
Unit 2 focuses on functions and their translations, reflections, and symmetries. Translations move the graph left/right or up/down, reflections flip or mirror the graph, and symmetries involve patterns that repeat on both sides of an axis. The document provides examples of translating and reflecting common parent functions like exponential and logarithmic functions. It also discusses symmetry in functions with respect to the y-axis (even functions), x-axis (odd functions), and origin. Homework problems are assigned from the textbook involving graphing functions and describing end behavior using limits.

1. Unit 2: FunctionsUnit 2: Functions

2. What do we need to do orWhat do we need to do or
change for Unit 2?change for Unit 2?
 Things to keep:Things to keep:  Things to change:Things to change:

3. TranslationsTranslations
 First, you have to know what the parentFirst, you have to know what the parent
functions look like!functions look like!
 Parent functions…Parent functions…

6. We did this in Alg 2!We did this in Alg 2!
 Graph the parent function and move it!Graph the parent function and move it!
 Ex:Ex:
 Left or right?Left or right?
 Up or down?Up or down?
 Flip or normal?Flip or normal?
2
( 4) 5y x= − − +

7. New to Pre-Calc…New to Pre-Calc…
 -f(x)-f(x)
 If there is a negative in the front it is aIf there is a negative in the front it is a
reflection over the x-axis. (flip)reflection over the x-axis. (flip)
 f(-x)f(-x)
 If there is a negative on theIf there is a negative on the “inside” it is a“inside” it is a
reflection over the y-axis. (mirror imaged)reflection over the y-axis. (mirror imaged)

8. GraphGraph
 Exponential ExampleExponential Example  Log ExampleLog Example
1
2 5x
y −
= + log( 5) 1y x= − +

9. Practice GraphingPractice Graphing
 2 1y x= − + − ( )
3
3 1y x= − − − +

10. SymmetrySymmetry

11. Symmetry - ExamplesSymmetry - Examples
 w/ respect to the y-axisw/ respect to the y-axis (EVEN)(EVEN)
 f(x) = xf(x) = x22
 w/ respect to the x-axisw/ respect to the x-axis (ODD)(ODD)
 x = yx = y22
 w/ respect to the originw/ respect to the origin
 f(x) = xf(x) = x33

14. Symmetry -Symmetry -
algebraicallyalgebraically
1.1.
2.2.
3.3.
3)( 2
−= xxf
22)( 2
−−= xxxf
2
3
4
)(
x
x
xf
−
=

15. HomeworkHomework
 P. 99 (47-54, 63-66P. 99 (47-54, 63-66 state endstate end
behavior using limits toobehavior using limits too))
 p. 109 (29-31p. 109 (29-31 no calc…justno calc…just
graphgraph, 35, 38, 39, 41), 35, 38, 39, 41)