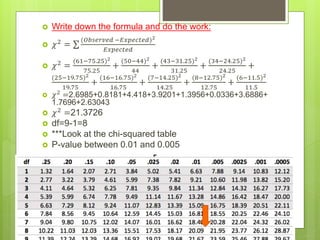
The document describes how an accountant wants to determine if a client has falsified tax information by looking for patterns in invoices. The accountant inspects a random sample of 250 invoices and compares the frequencies of first digits to the probabilities predicted by Benford's Law using a chi-squared test. The results show a p-value between 0.01 and 0.005, below the significance level of 0.05. Therefore, the accountant can conclude the invoices are inconsistent with Benford's Law and suspect fraudulent activity.

1. Do this problem as practice and then check
yourself!
 An accountant wants to determine if a client
has “faked” some of their tax return
information. In order to do that, they can look
for patterns that aren’t present in legitimate
records. It is a fact that the first digits of
numbers in legitimate records often follow a
model known as Benford’s Law. Benford’s
Law gives this probability distribution for X.
(continue on next slide)
Frist Digit
(X)
1 2 3 4 5 6 7 8 9
P(X) 0.301 0.176 0.125 0.097 0.079 0.067 0.058 0.051 0.046

2. Problem (cont.)
 This accountant inspects a random sample of 250
invoices from their client before accusing them of
committing fraud. The table below shows the
sample data.
 Are these data inconsistent with Benford’s law?
Perform the appropriate significance test at the
𝛼 = 0.05 level to support your answer.
Frist Digit
(X)
1 2 3 4 5 6 7 8 9
P(X) 0.301 0.176 0.125 0.097 0.079 0.067 0.058 0.051 0.046

3. Before you continue…
 Remember, you must find the actual expected
counts from the proportions given in the
probability model!
 NOW – work the problem on your own
paper before continuing.
 You can check your answers on the following
slides.

4.  State hypotheses:
 𝐻 𝑜: 𝑝1 = 0.301, 𝑝2 = 0.176, 𝑝3 = 0.125, 𝑝4 = 0.097
𝑝5 = 0.079, 𝑝6 = 0.067, 𝑝7 = 0.058, 𝑝8 = 0.051, 𝑝9 = 0.046
 𝐻 𝑎: at least one of the proportions is incorrect

5.  Check conditions:
 Random: this was stated in the problem - random
sample of 250 invoices
 Large Sample Size: in order to do this we must
check each expected count to see if it is at least
5
Every expected count is at least 5, so it
meets this condition
 Independent: there are more than 2500 invoices
from this client, so it meets the 10% rule
.301(250)=75.25 .097(250)=24.25 .058(250)=14.5
.176(250)=44 .079(250)=19.75 .051(250)=12.75
.125(250)=31.25 .067(250)=16.75 .046(250)=11.5

6.  Write down the formula and do the work:
 𝜒2 =
(𝑂𝑏𝑠𝑒𝑟𝑣𝑒𝑑 −𝐸𝑥𝑝𝑒𝑐𝑡𝑒𝑑)2
𝐸𝑥𝑝𝑒𝑐𝑡𝑒𝑑
 𝜒2 =
(61−75.25)2
75.25
+
(50−44)2
44
+
(43−31.25)2
31.25
+
(34−24.25)2
24.25
+
(25−19.75)2
19.75
+
(16−16.75)2
16.75
+
(7−14.25)2
14.25
+
(8−12.75)2
12.75
+
(6−11.5)2
11.5
 𝜒2 =2.6985+0.8181+4.418+3.9201+1.3956+0.0336+3.6886+
1.7696+2.63043
 𝜒2 =21.3726
 df=9-1=8
 ***Look at the chi-squared table
 P-value between 0.01 and 0.005

7.  Conclusion:
 Since the p-value is less than 𝛼 = 0.05 then
we reject 𝐻 𝑜.
 We have statistically significance evidence to
say that the invoices are inconsistent with
Benford’s Law, and therefore the accountant
should be suspicious of fraudulent activity.
 The largest contributors are the numbers that
start with the number 3.