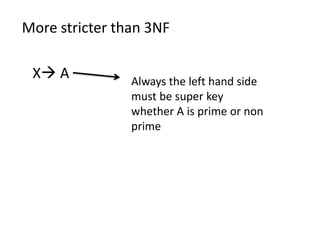
This document discusses database normalization forms and dependencies. It covers: - The two levels of discussing relation schema quality (logical and implementation) - Informal measures of quality like semantics, redundancy, NULL values, and spurious tuples - Functional dependencies, inference rules, closure, and finding a minimal cover - First, second, third, and BCNF normal forms and their definitions/conditions - Non-prime and prime attributes - Other dependencies like multivalued, join, and their relationships to higher normal forms.

2. There are two levels at which we discuss the goodness of
relation schema
•Logical (or Conceptual)Level
•Implementation (or storage ) Level

4. 4 Informal measures of quality for
relation schemas are
I. Semantics of the attribute
• interpretation of attribute values
from tuples
II. Reducing redundant information in tuples
• minimize the storage space used by
the base relation
• Problem of update anomalies
• Insertion of anomalies
• Deletion of anomalies
• Modification of anomalies

5. iii. Reducing the NULL values in the tuples
• Waste space at storage levels
• Also lead to problems with understanding
the meaning of attributes (ex:count,join )
iv. Disallowing the possibility of generating
spurious tuples
• Seems to be genuine but it is false

9. • Most important concept in relational schema design theory.
• A functional dependency is a constraint between two set of
attributes from the database.
• it is denoted by X  Y(functional dependency from x to y or y
is functionally dependent on X.)
• i.e. Y component of a tuple in r depend on , or are
determined by , the values of the Y component.
•A functional dependency is a property of the of the semantics
or meaning .

11. Inference ???
•Dept_no  Mgr_SSN , each department has one manager
• Mgr_SSN  Mgr_phone : Each manage has a unique phone number
• then we can infer Dept_no  Mgr_phone

12. closure ???
Closure : includes all dependencies that can
be inferred from the given set F, it is denoted
by F+
Let us see some example on board

13. To determine a systematic way to infer dependencies,
we use inference rules that can be used to infer new
dependencies
The notation F XY means the functional
dependency XY is inferred from functional
dependencies F.

14. Trivial
otherwise
Inference rules for functional dependencies are :
Non-Trivial
• IR1 (reflexive rule)
: If Y subset-of X,
then X  Y
•IR2 (augmentation rule)
: If X -> Y, then XZ -> YZ
•IR3 (transitive rule)
:If X Y & Y Z, then
XZ
•IR4 (decomposition ,or projective rule)
: If X YZ then X Y
•IR5 (Union or additive rule)
: If XY,XZ then XYZ
•IR6 (pseudo transitive rule)
: If XY,WYZ then
WX  Z

15. Inference rules IR1 through IR3
are sound and complete
Dependency that we
can infer from F by
using IR1 to IR3 holds
every relation state r
of R that satisfies the
dependencies in F.
Using IR1to IR3
repeatedly to infer
dependencies until no
more dependencies
can be inferred from F
The closure of F , can be determined from F by using
inference rules IR1 to IR3 are known as Armstrong ‘s
inference rules.

17. Cover : A set of functional dependencies F is said
to cover another set of dependencies E if every
FD in E is also in F +.
Or we can say that E is covered by F.
Two sets of functional dependencies E and F are
equivalent if E += F +
.

19. Minimal cover : minimal cover of a functional dependencies E
is a set functional dependencies F that satisfies the property
that every dependency in E is in the closure of F+ of F.
•Every set of FDs has an equivalent minimal set
•There can be several equivalent minimal sets
•There is no simple algorithm for computing a minimal
set of FDs that is equivalent to a set F of FDs
•To synthesize a set of relations, we assume that we
start with a set of dependencies that is a minimal set

20. Algorithm
Finding a Minimal cover F for a set of functional dependencies E
• Set F:= E
• Replace each functional dependencies X{A1,A2,. . . .,An}
in F by the n functional dependencies X A1,XA2,. ..
.,XAn.
• For each functional dependencies X A in
For each attribute B that is an element of X
• if {F – {XA}} U {(x-{B}) a} }
CANONICAL form

21. Find minimum cover for E
{B A, DA,ABD}
Find minimum cover for E
{AD,BCA,BCD,CB,EA,ED}
Find minimum cover for E
{ AB -> C, C -> A, BC -> D, ACD -> B, D -> E, D ->
G, BE -> C, CG -> B, CG -> D, CE -> A, CE -> G}

22. Find minimum cover for E
{noname
noage
no,nameage
noage,name}

25. •First proposed by Codd (1972)
•Initially proposed first ,second and
3NF
• later Boyce and Codd proposed
BCNF
• later 4th and 5th NF are proposed
based on the concept of multivalued dependency and join
dependencies

26. Advantages
•Minimizing redundancy
•Minimizing insertion , deletion, and
modification of anomalies
Normal form a relation refers to the highest
normal form condition that it meets, and hence
indicate the degree to which it has been
normalized

27. Non-prime attribute
A non-prime attribute is an attribute that does not occur in any
candidate key.
Employee Address would be a non-prime attribute in the
"Employees' Skills" table.
Prime attribute
A prime attribute, conversely, is an attribute that does occur in
some candidate key.

29. •Disallow multi valued attributes and composite attributes
• it states that domain of an attributes must include only
atomic (simple, indivisible)values.
•Ex: address

31. Partial key

32. Must be in 1NF

33. Full functional dependency : A functional dependency X Y is a
FULL FUNCTIONAL dependency if removal of any attribute A from X
means that dependency does not hold any more;
Partial dependency : A functional dependency X Y is a partial
dependency if some attribute A in X can be removed from X and
dependency still holds
Def : A relation schema R is in 2NF if every non
prime attribute A in R is fully functionally
dependent on the primary key of R

36. •it must be in 2NF
•It is based on the concept of transitive dependency
• XY ,Y Z then XZ
DEF : A relation schema R is in 3NF if it
satisfies 2NF and no prime attribute of R is
transitively dependent on the primary key
X A
If A is non prime attribute
then X must be super key

39. More stricter than 3NF
X A
Always the left hand side
must be super key
whether A is prime or non
prime

40. Here {student, course  instructor}
{instructor course}
It is 3NF but not BCNF

41. BCNF is
More stricter than 3NF
In BCNF must check TWO conditions
• X Y allowed ,if it is trivial functional dependency
OR
• X is a super key for schema R

42. A 3NF table which does not have
multiple overlapping candidate keys
is guaranteed to be in BCNF
Ex: 3NF but not BCNF
Court
Start Time
End Time
Rate Type
1
09:30
10:00
SAVER
1
11:00
12:00
SAVER
1
14:00
15:30
STANDARD
2
10:00
11:30
PREMIUM-B
2
11:30
13:30
PREMIUM-B
2
15:00
16:30
PREMIUM-A
2
9:30
10:00
PREMIUM-A

43. Here the candidate keys are
S1: {COURT,START TIME}
S2:{COURT,END TIME}
S3:{RATE TYPE,START TIME}
S4:{RATE TYPE, END TIME}
Here no non prime attributes , all are prime attribute
belongs to some candidate key.
So the table is 2NF and 3NF.but not in BCNF.

44. Here no non prime attributes , all are prime attribute
belongs to some candidate key.
So the table is 2NF and 3NF,but not in BCNF because of
rate type  court.

45. Now it is in BCNF Rate Types
Rate Type
SAVER
STANDARD
Court
1
1
Member Flag
Yes
No
PREMIUM-A
PREMIUM-B
2
2
Yes
No
Today's Bookings
Rate Type
SAVER
SAVER
STANDARD
PREMIUM-B
PREMIUM-B
PREMIUM-A
Start Time
09:30
11:00
14:00
10:00
11:30
15:00
End Time
10:30
12:00
15:30
11:30
13:30
16:30

46. Problems when using BCNF
Person
Shop Type
Nearest Shop
Thankam
Optician
Eagle Eye
Meenu
Hairdresser
Snippets
Pretty
Bookshop
Merlin Books
Sreedevi
Bakery
Sree bakers
Sreedevi
Hairdresser
Sweeney
Sreedevi
Optician
Eagle Eye
Dependency:
A, B  C
CB
Not BCNF

47. Shop Near Person
Person
Shop
Thankam
Meenu
Pretty
Eagle Eye
Sreedevi
Sreedevi
Sreedevi
Sree Bakers
Snippets
Merlin Books
Sweeney
Eagle Eye
Shop
Shop
Shop Type
Eagle Eye
Optician
Snippets
Hairdresser
Merlin Books
Bookshop
Sree Bakers
Bakery
Sweeney
Hairdresser

48. Problem : It allow us to record data such as,a
person’s multiple shops with same type ,It
violates the dependency
{person,shoptype}{shop}
So BCNF is not always possible

49. (Lets do some problems)

51. NON ADDITIVE (LOSELESS) JOIN DEPENDENCY
•Which ensures that no spurious tuples are generated
when a NATURAL JOIN operation is applied to the
relations in the decomposition
• lossless refers to loss information ,not to loss of
tuples.

52. Example of lossy decomposition
Decomposition
Original table
A
1
1
1
B
1
1
2
C
1
2
1
A
C
1
1
1
2
1
2
1
1
2
2
B
1
1
1
1
B
1
A
1
A
1
C
2
1
2
Reconstruction

53. MULTIVALUED DEPENDENCY
: A consequence of first normal form, Which disallows an attribute
have a set of values
: A multivalued dependency is a special case of a join dependency,
Course
Book
Lecturer
AHA
Silberschatz
John D
AHA
Nederpelt
William M
AHA
Silberschatz
William M
and equivalently
AHA
Nederpelt
John D
{course}  {lecturer}.
AHA
Silberschatz
Christian G
AHA
Nederpelt
Christian G
OSO
Silberschatz
John D
OSO
Silberschatz
William M
{course} {book}

54. Definition for 4th Normal Form
A relation schema R is in 4NF with respect to a set
of dependencies F (that include functional
dependencies and multivalued dependencies ),if for
every non trivial multivalued dependency X Y
in F closure,X is a super key of R.

57. •In dependency theory, a join dependency is a
constraint on the set of legal relations over a
database scheme. A table T is subject to a
join dependency if T can always be recreated by
joining multiple tables each having a subset of
the attributes of T.
• If one of the tables in the join has all the
attributes of the table T, the join dependency is
called trivial

58. •If JOIN dependency is present carry out a
multiway decomposition in to 5th Normal
form
•Such dependency is very peculiar semantic
constraint, that is very difficult to detect I
practice. So 5NF very rarely done in practice.