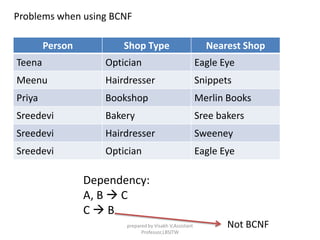
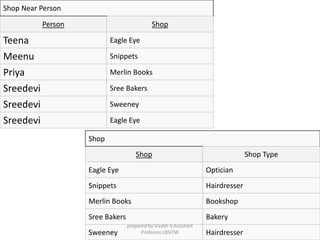
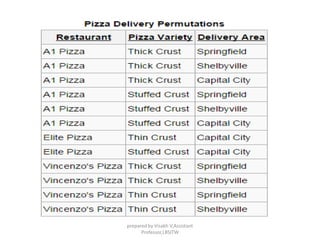
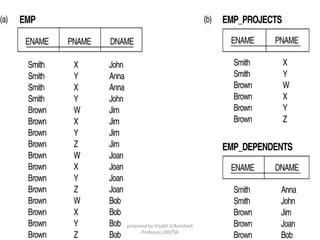
The document discusses functional dependencies and their importance in relational schema design, highlighting measures of schema quality and various levels of normal forms. It explains concepts such as minimal cover, Armstrong's inference rules, and the implications of different normal forms (1NF, 2NF, 3NF, BCNF, 4NF, and 5NF) on database structures. Additionally, it addresses the issues related to redundancy, anomalies, and the conditions under which certain functional and multivalued dependencies hold.