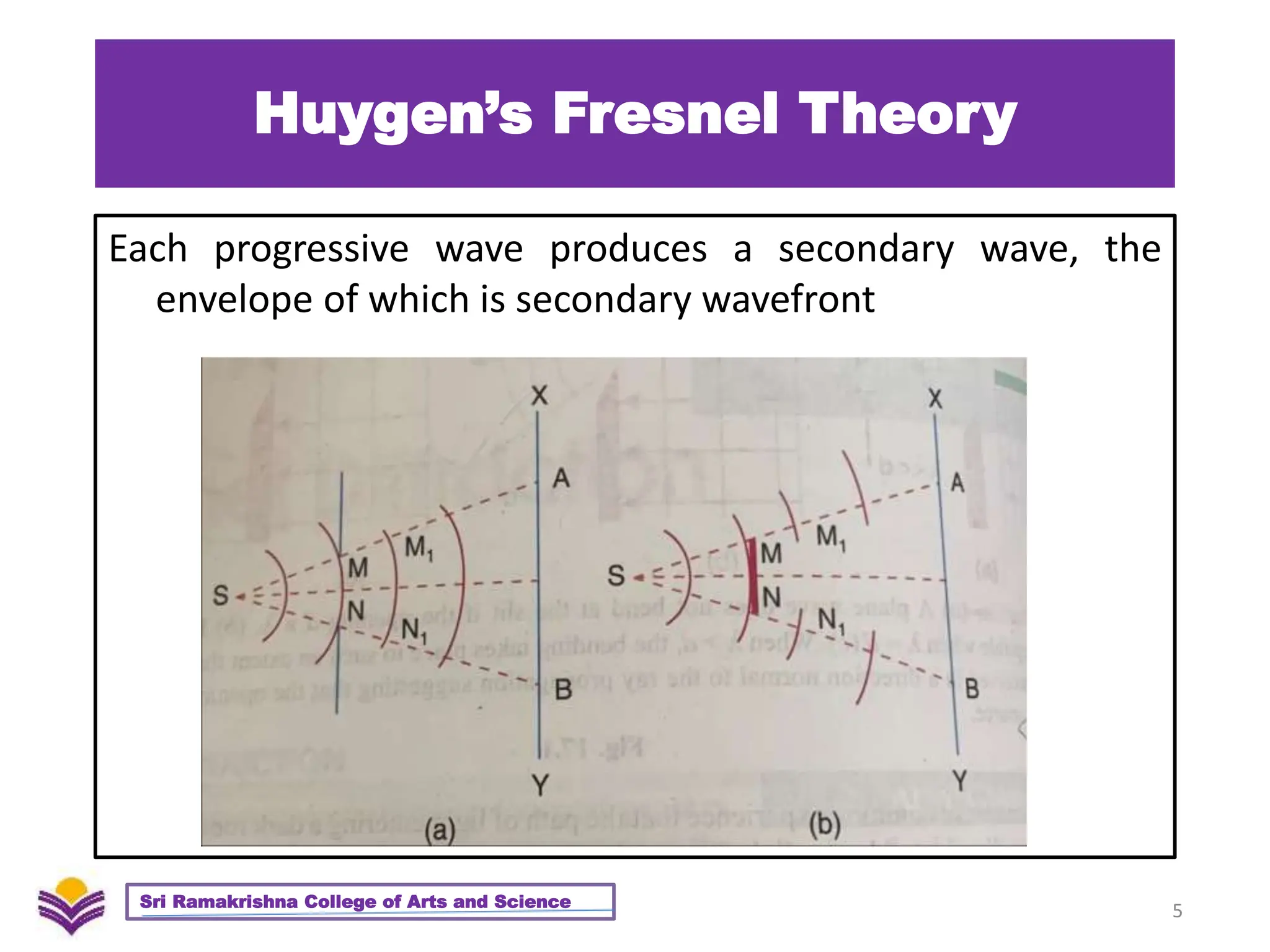
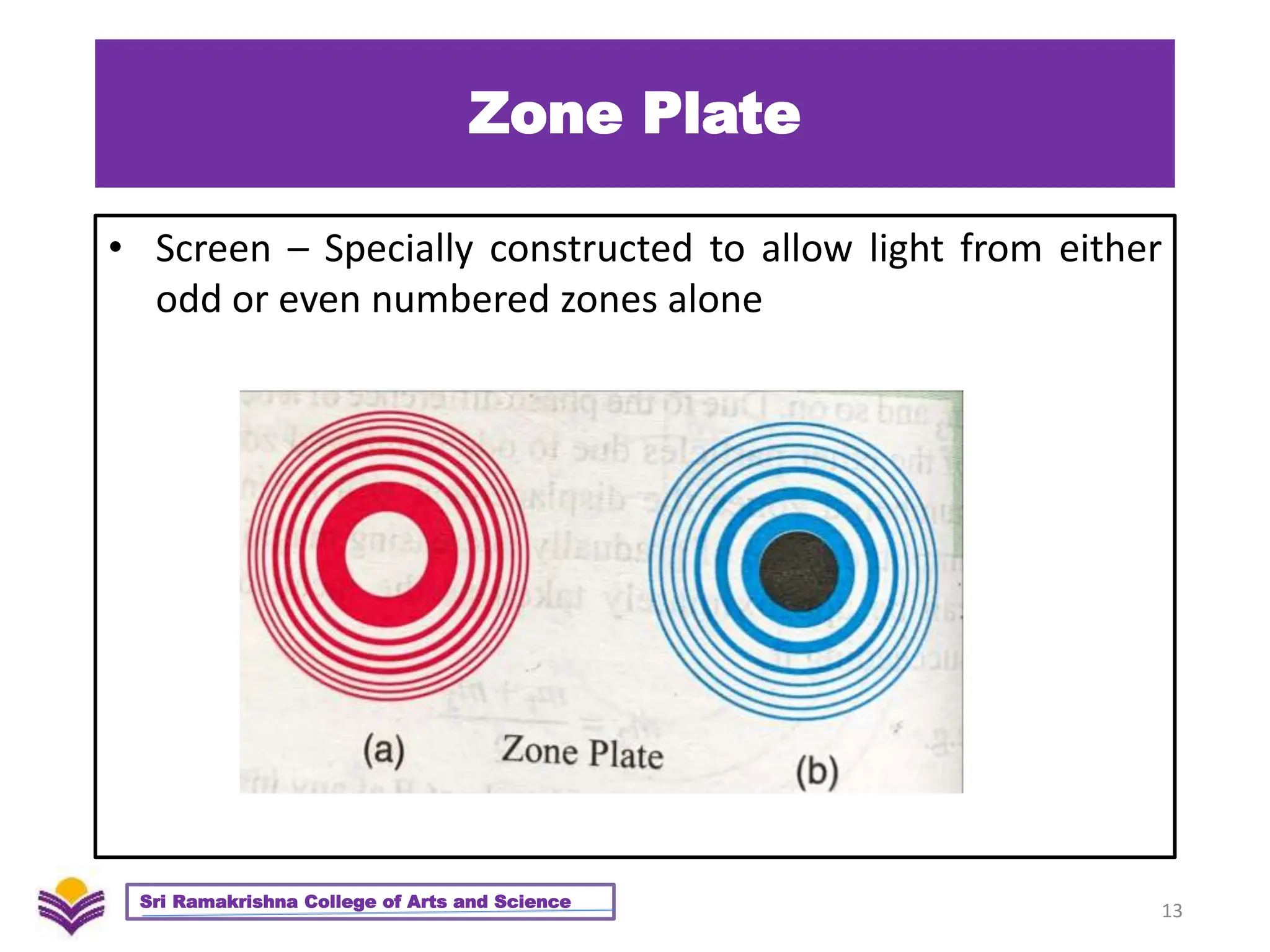
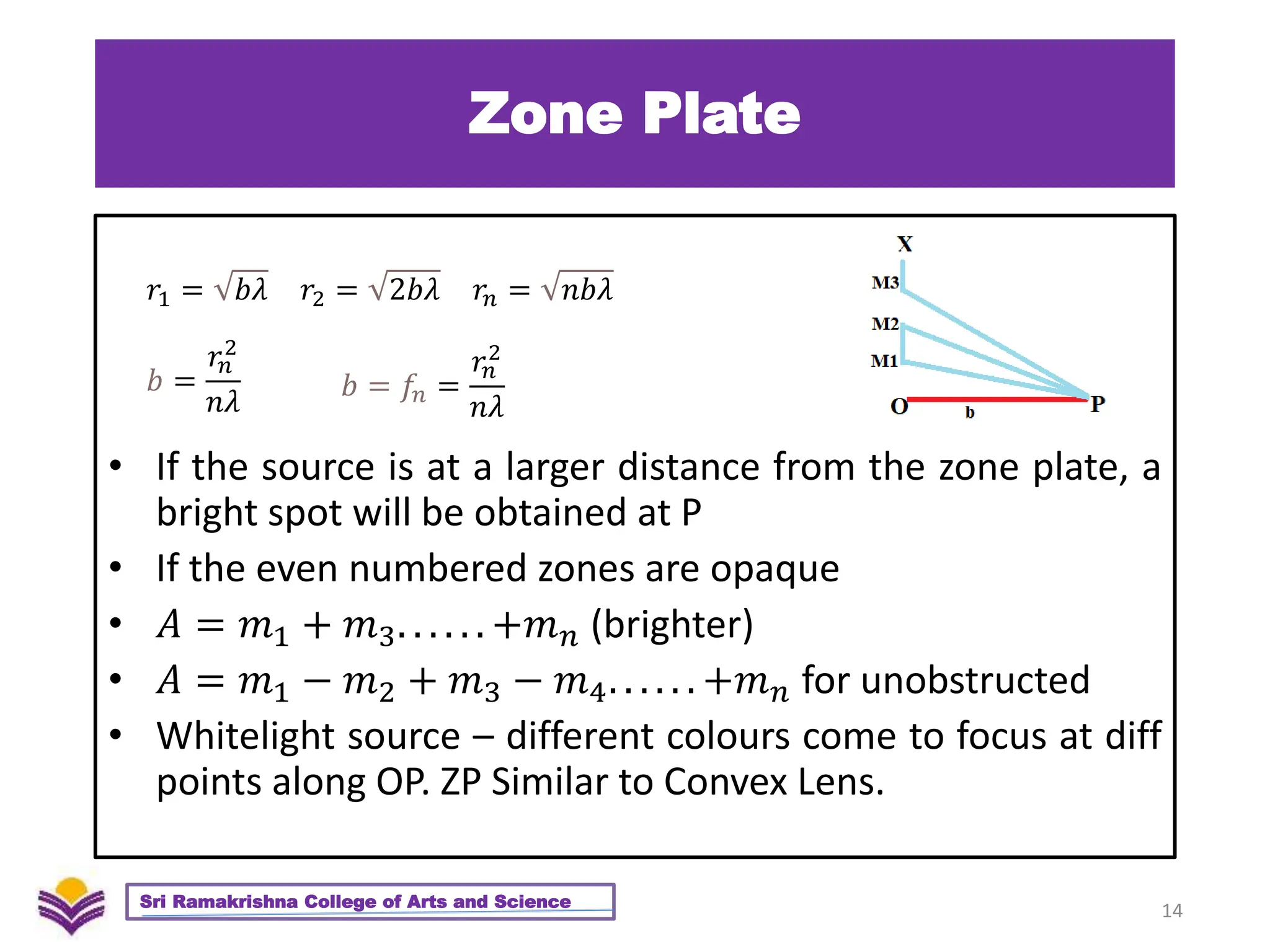
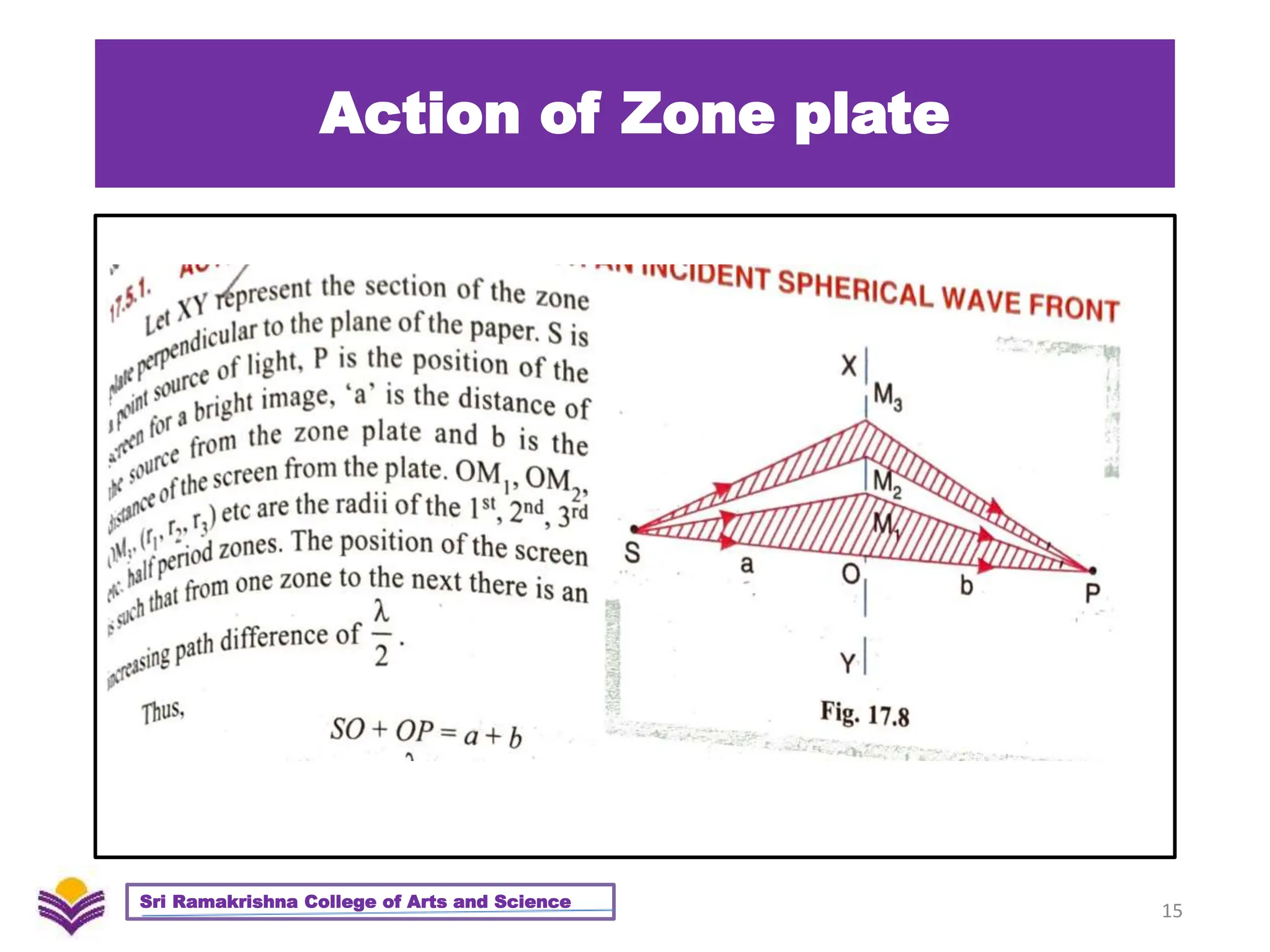
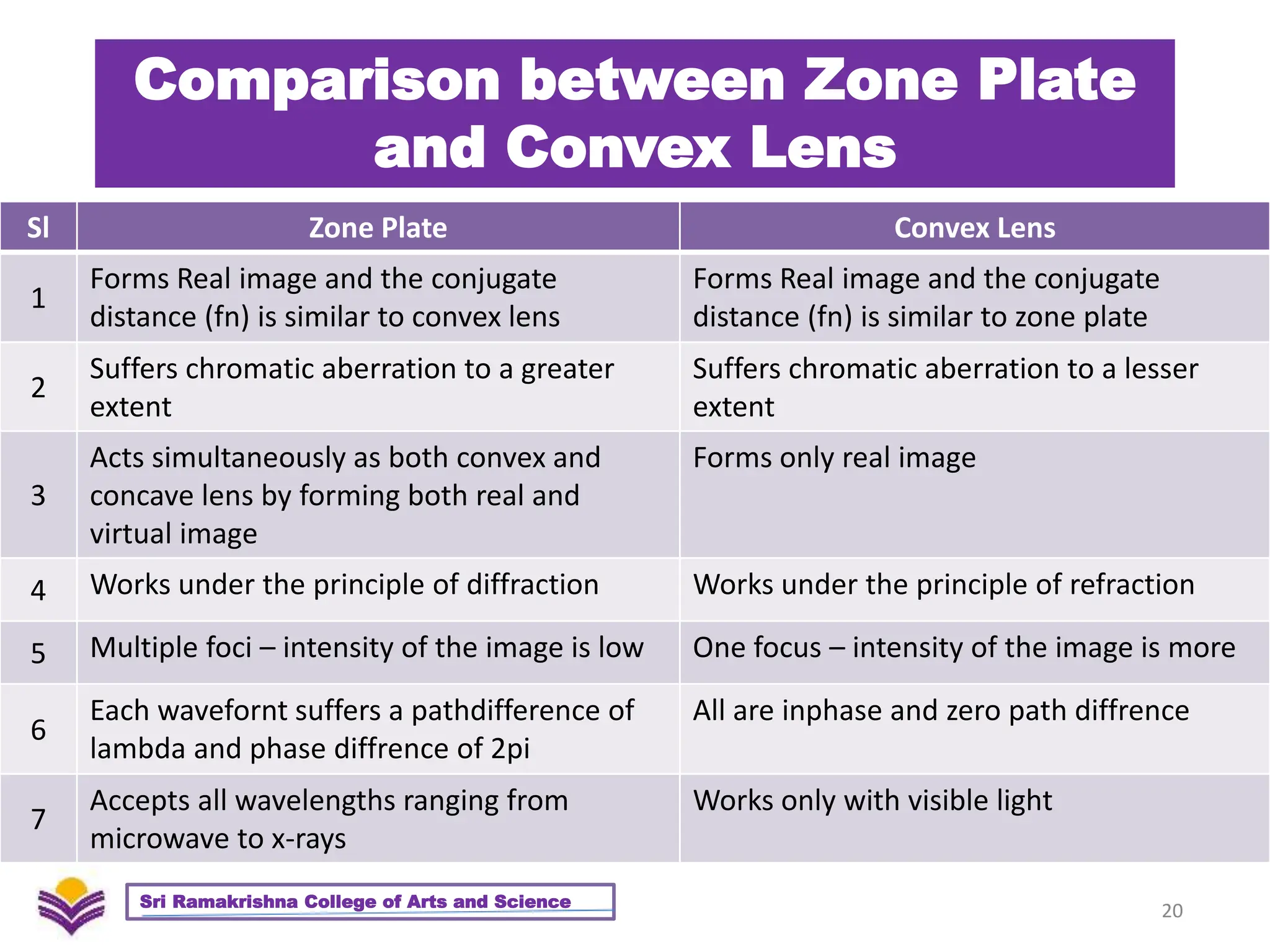
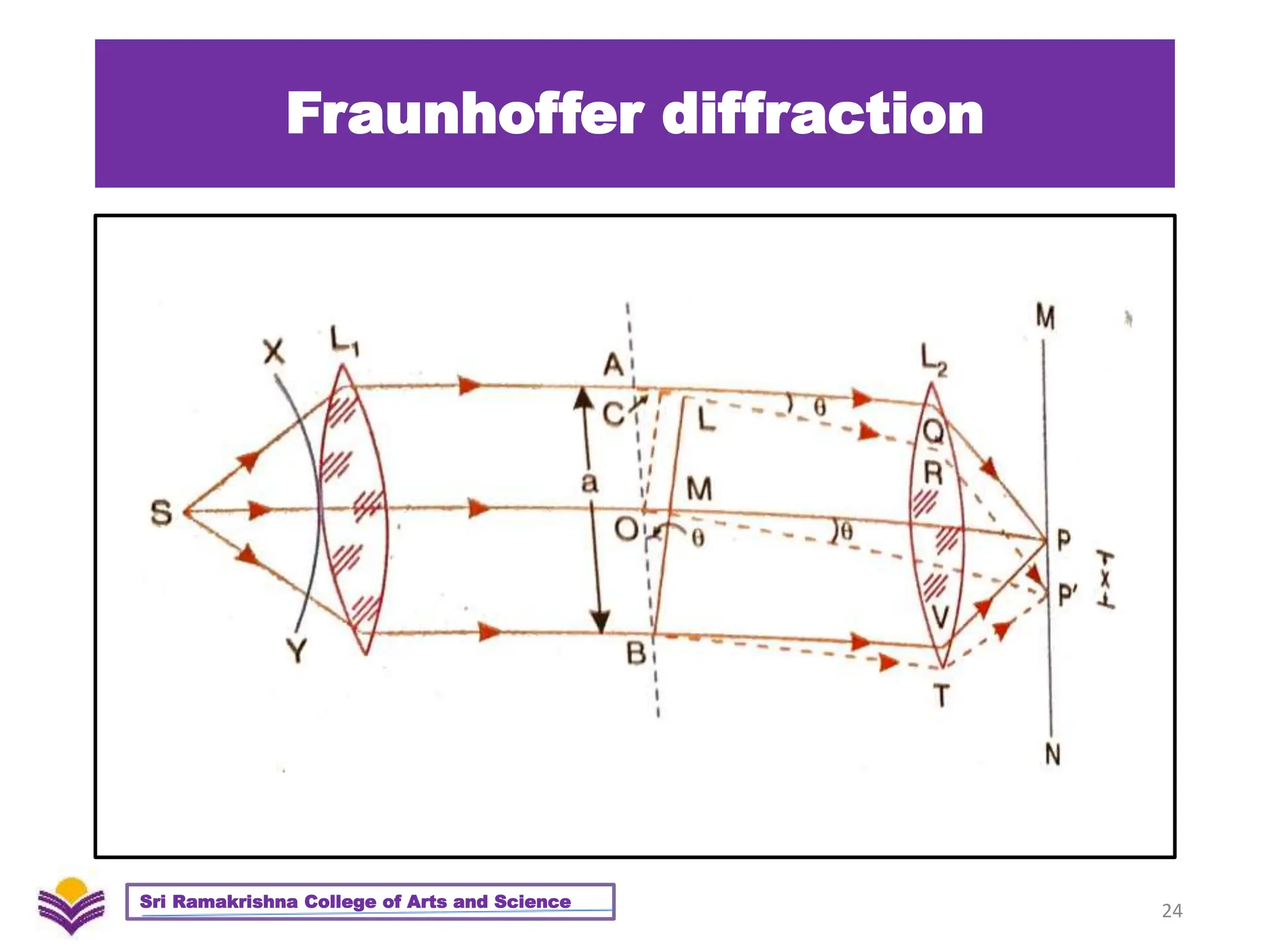
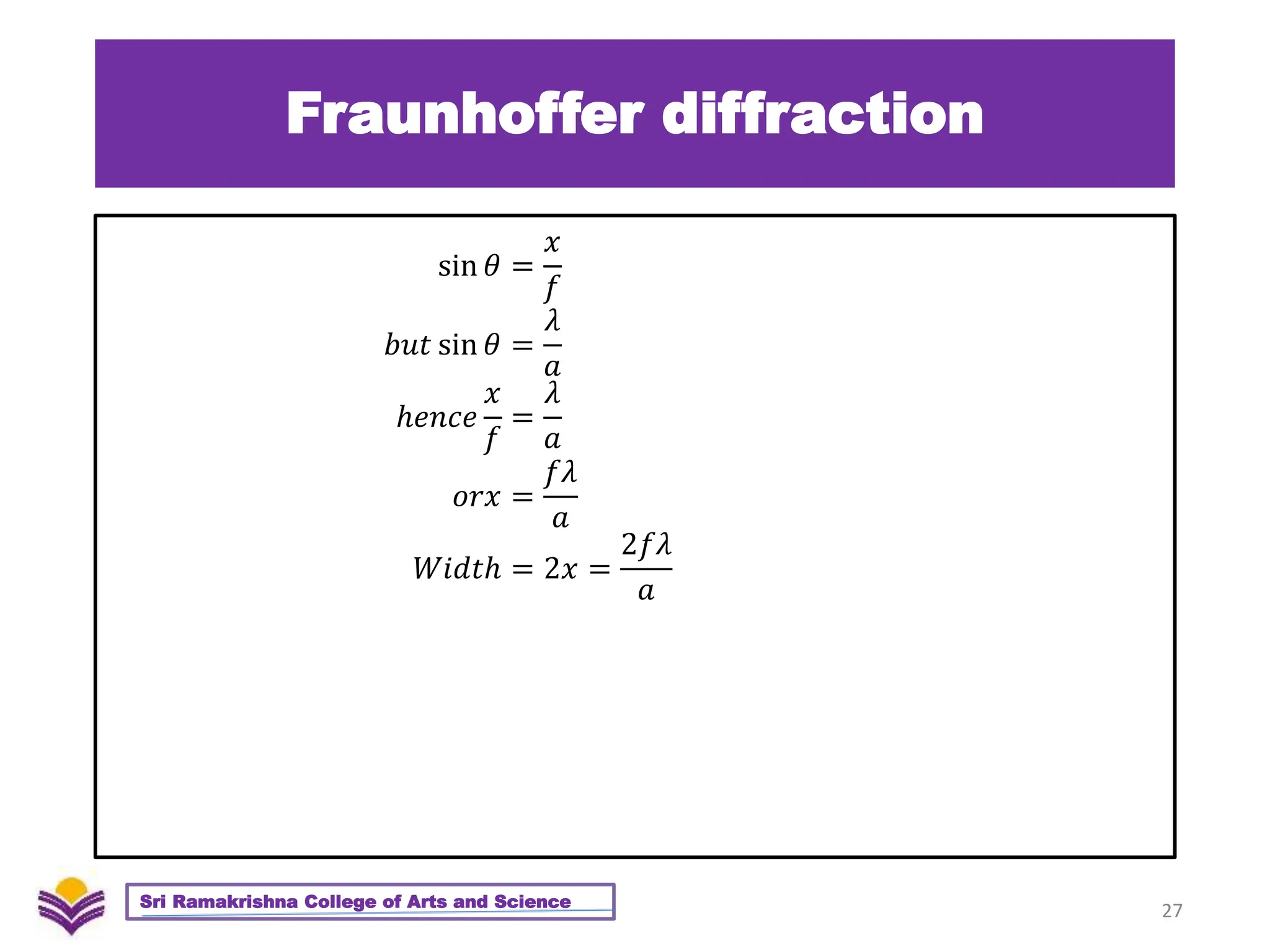
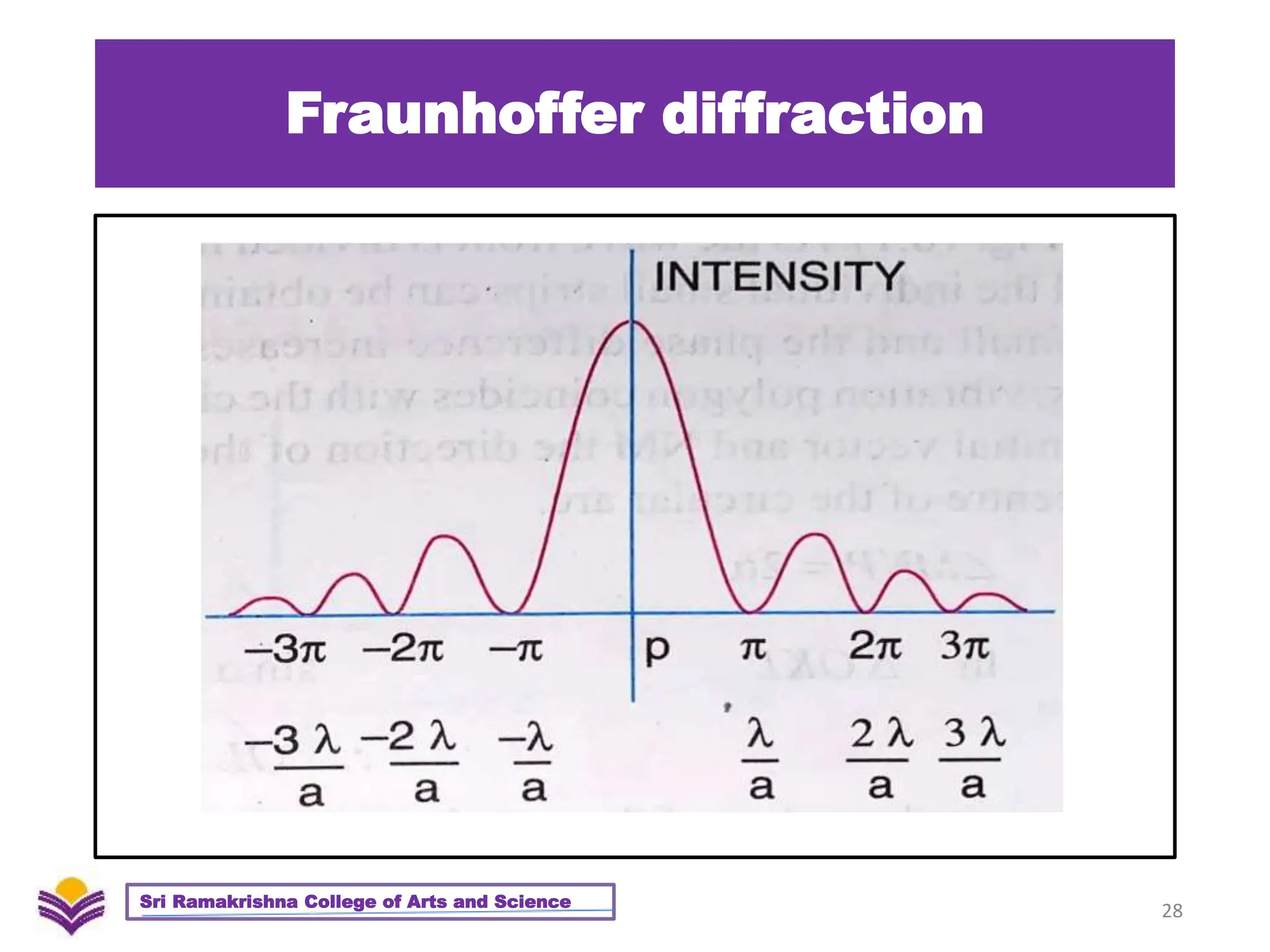
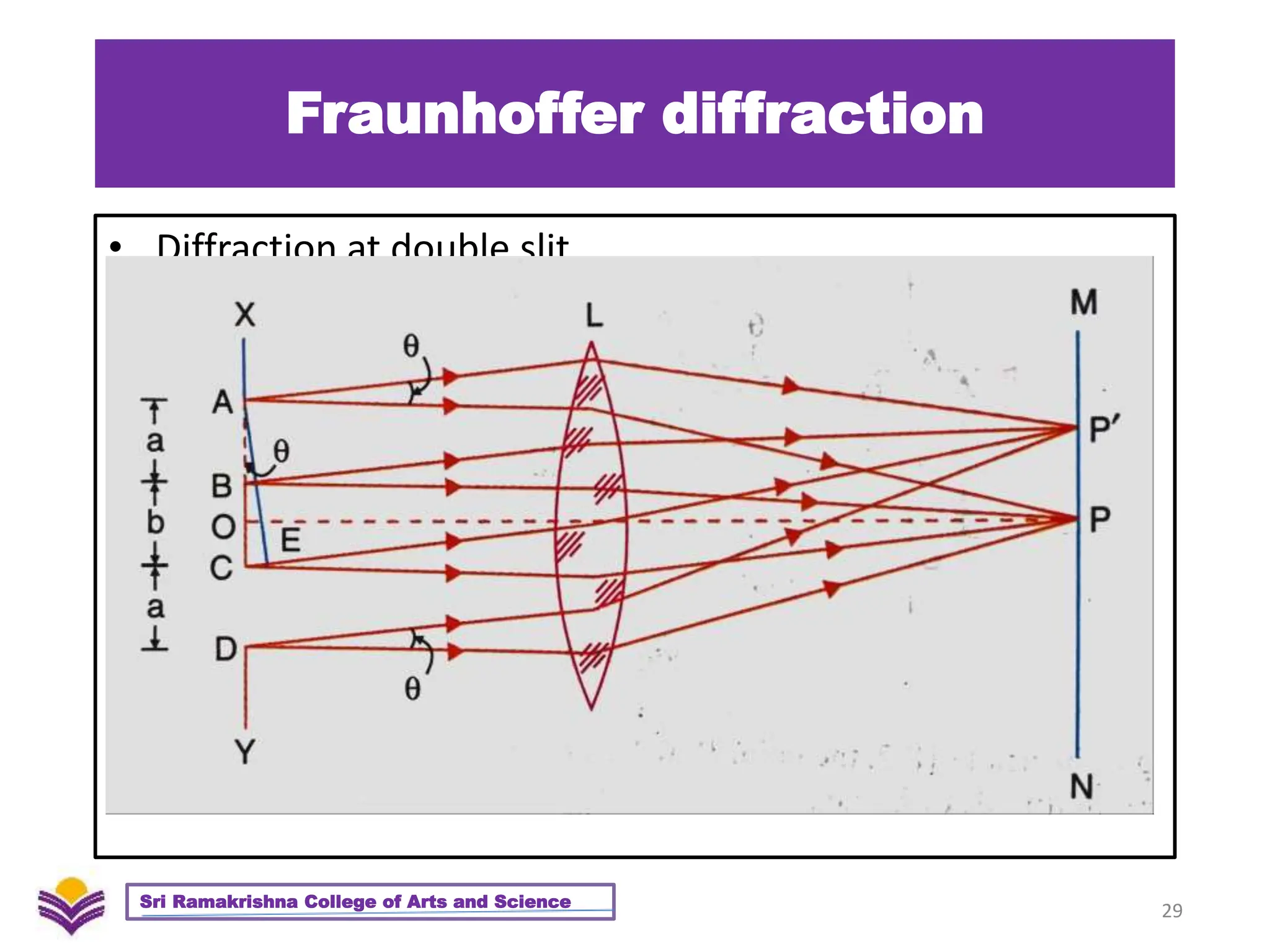
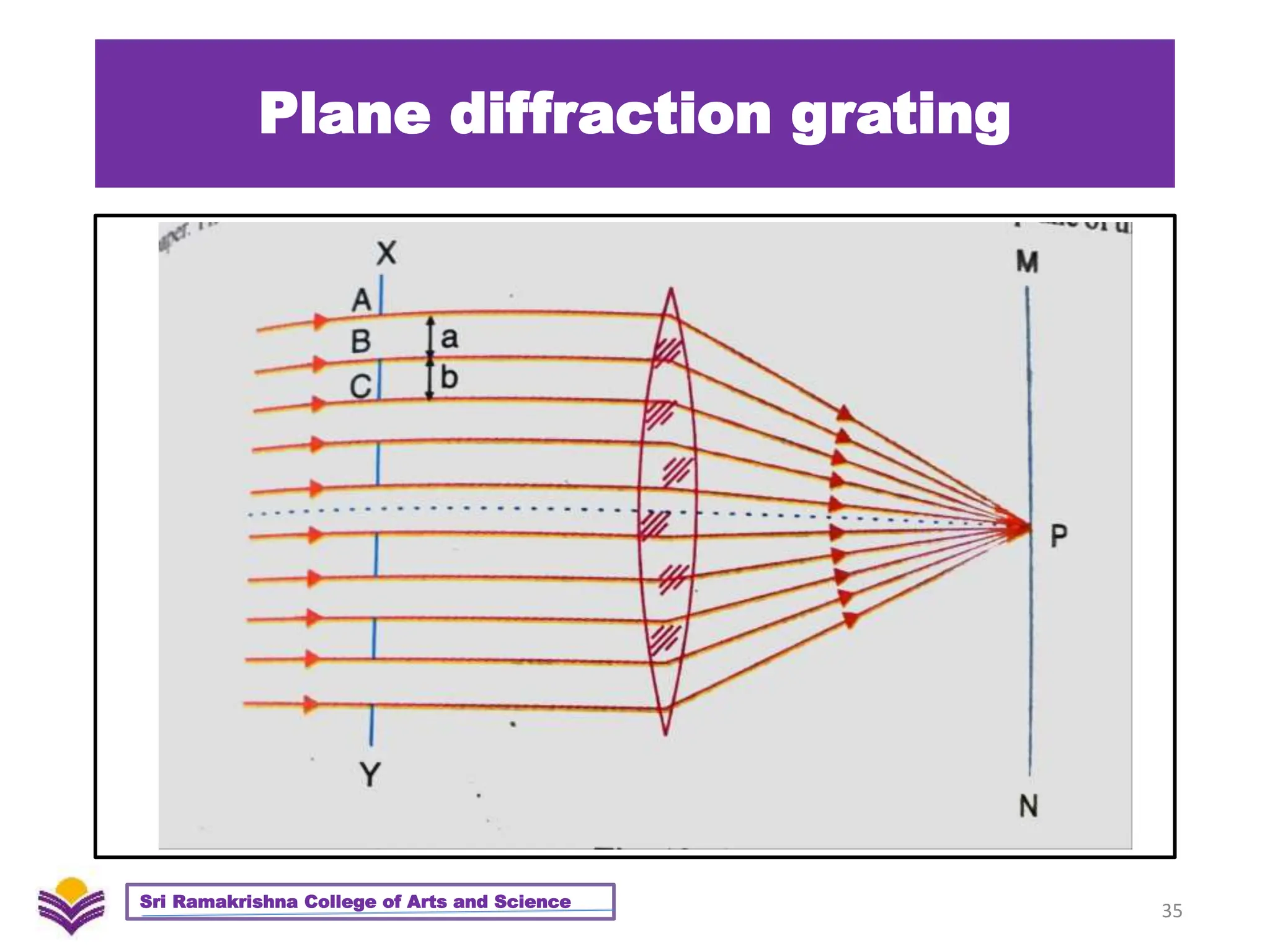
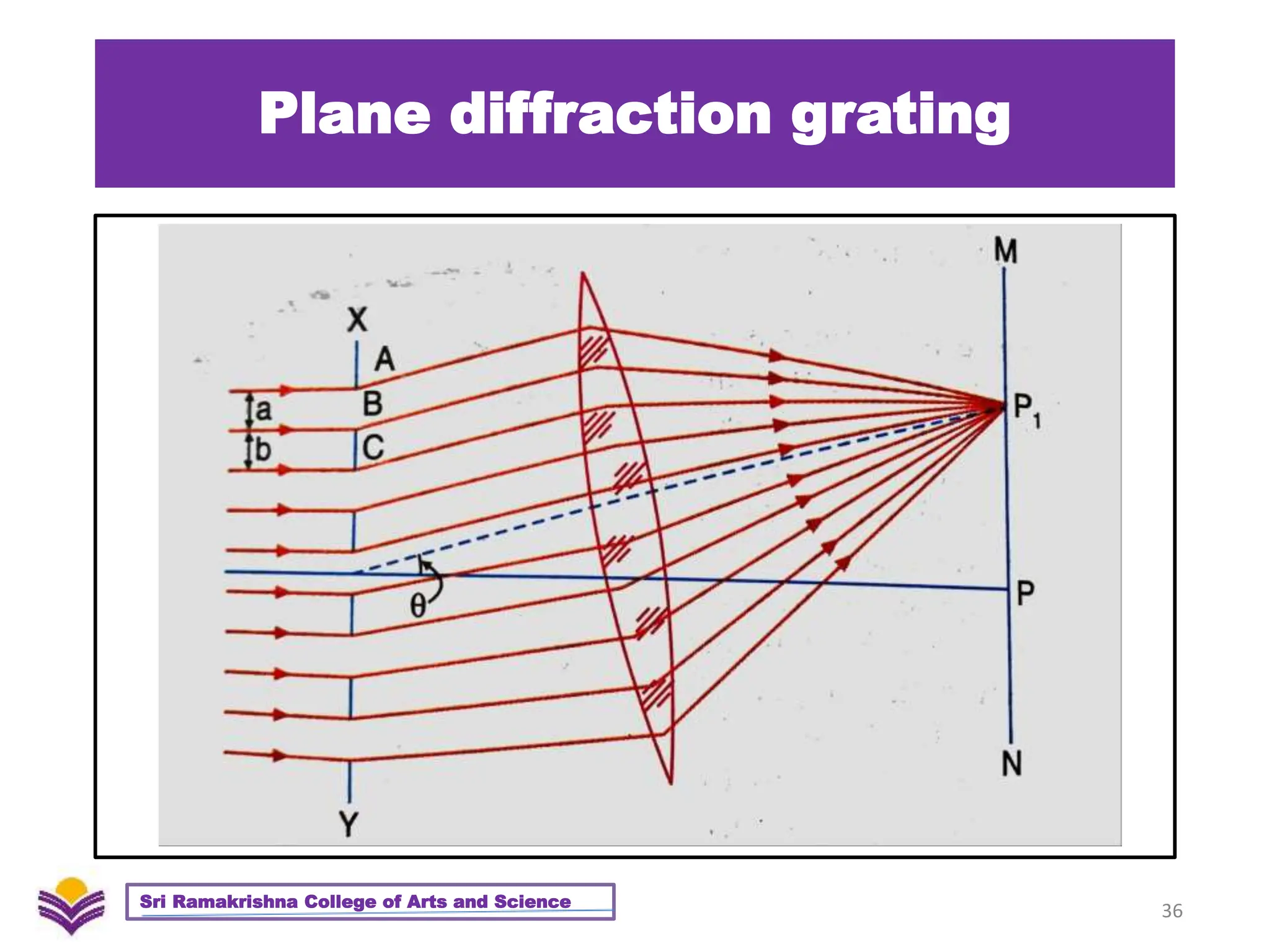
The document provides a detailed overview of diffraction, including Huygens-Fresnel theory, Fresnel's assumptions, and the differences between interference and diffraction. It discusses phenomena such as diffraction patterns from slits and edges, Fraunhofer diffraction, and the use of zone plates in optics. Furthermore, it compares the behavior of zone plates and convex lenses, and explores plane diffraction gratings and their principles.