This document details an experiment conducted by the Petroleum Engineering Department at Soran University to measure fluid flow rate and demonstrate Bernoulli’s theorem using a hydraulic bench unit. It includes an introduction to the equipment, procedures for the experiments, calculations for fluid flow rates and Bernoulli’s theorem, as well as data tables and discussions on the results. The findings confirm the theoretical relationships between pressure, velocity, and elevation of flowing fluids.

1. 1
Soran University
Faculty of Engineering
Petroleum Engineering Department
Fluid Flow Rate & Bernoulli’s Theorem Demonstration
Supervised by: Dr. Dara Khalid Khidir
Prepared by: Raboon Redar Mohammed
January 16th 2021

2. 2
Contents
Aim ....................................................................................................................................................................3
Introduction........................................................................................................................................................3
Hydraulic Bench Unit:...................................................................................................................................3
Description unit of (Bernoulli’s Theorem Demonstration): ..........................................................................4
Procedure of the Experiment (fluid flow rate)...................................................................................................5
Procedure of the Experiment (Bernoulli’s Theorem Demonstration)................................................................5
Calculation of (fluid flow rate) ..........................................................................................................................6
Table of reading (fluid flow rate)...................................................................................................................6
Table of calculation (fluid flow rate).............................................................................................................6
Calculation of Bernoulli’s Theorem Demonstration..........................................................................................7
Table of readings (Bernoulli’s Theorem Demonstration)..............................................................................7
Table of Calculation (Bernoulli’s Theorem Demonstration).........................................................................7
Discussion (fluid flow rate) ...............................................................................................................................8
Discussion (Bernoulli’s Theorem Demonstration) ............................................................................................9
References........................................................................................................................................................10

3. 3
Aim
The aim of the fluid flow rate experiment is to measure the fluid flow rate using a device called the hydraulic
bench unit, which is also used to prove the Bernoulli’s Theorem Demonstration by measuring the overall
pressure of the fluid flow.
Introduction
Hydraulic bench (which is fitted with a lever shaped like a seesaw) is used to measure the actual water
discharge measured in experiments where the actual discharge is less than the theoretical discharge. The lever
ties the load with a water discharge tub. (hydraulic bench tools in hydraulics science as well as research functions
and processes. — Steemit, 2021) A reliable laboratory facility that allows complex fluid mechanics lab tests, is
the Basic Hydraulic bench and the numerous additional modules that are available. The hydraulic bench unit
provides basic pumping facilities and a volumetric calculation of the water source for which all additional
accessories and experiments are used. The working surface of the device is in fiberglass, molded to have a
recessed area where tests can be carried out. Volume and period of reading may be used to evaluate the flow
rate. (Basic Flow Experiments Bench: Hydraulics Bench and Accessories, 2021)
Hydraulic Bench Unit:
1- Volumetric measuring tank with channel; 2- Remote sight gauge
3- Sliding valve 4- Sump tank
5- Drain cock 6- Submersible motor driven pump
7- Water supply for accessories with pump 8- Flow control valve
9- Overflow pipe 10- Switch box
11- Discharge cap 12- Water supply connection for accessories without pump

4. 4
Description unit of (Bernoulli’s Theorem Demonstration):
Bernoulli's hypothesis show device is the test device which could be estimated through a venturi tube with 6
focuses of weight measurements. A panel with 6 water weight gages, show the 6 inactive weights. In various
areas in the venturi tube, the calculation of height and weight can also be seen on a single water weight gage.
Estimation is a measure that in relation to the venturi tube may be movably shifted. A compression device is
used to correct the test and the pressure driven seat provides the water. (F1-15 Bernoulli's Theorem Demonstration
- Armfield, 2021).
1. Assembly boar. 2. Single water pressure gauge. 3. Discharge pipe. 4. Outlet ball cock.
5. Venturi tube with 6 measurement points. 6. Compression gland. 7. Probe for measuring
overall pressure (can be moved axially) 8. Hose connection, water supply.
9. Ball cock at water inlet 10. 6-fold water pressure gauge (pressure distribution in venturi tube).
The relationship between these three types of energy was first defined by Daniel Bernoulli. Bernoulli's
streamline flow theorem is based on three assumptions: continuous flow, incompressible fluid and fluid
friction loss. The hypothesis of Bernoulli in connection with a streamline relies on three suspicions: unfiltered
stream, incompressible liquid and no liquid molding misfortunes. In this test the validity of the condition of
Bernoulli will be confirmed. The theorem of Bernoulli can be stated and communicated as follows for any
two focuses that are found on the same stream. (Ahmari and Kabir, 2021).
𝑃1
𝜌𝑔
+
𝑣12
2𝑔
+ 𝑧1 =
𝑃2
𝜌𝑔
+
𝑣22
2𝑔
+ 𝑧2
- P: pressure, g: acceleration due to gravity,
- v: fluid velocity, z: vertical elevation of the fluid.

5. 5
The hydrostatic pressure (P) along the flow is measured by manometers tapped into the duct. The pressure
head (h), thus, is calculated as:
ℎ𝑠 =
𝑃
𝜌𝑔
Therefore, Bernoulli’s equation for the test section can be written as:
ℎ1 +
𝑣12
2𝑔
= ℎ2 +
𝑣22
2𝑔
= 𝐻
in which
𝑣2
2𝑔
is called the velocity head (hd)
z is called potential head
Total head (ht) may be measured by the traversing hypodermic probe.
ℎ𝑚 = ℎ +
𝑣2
2𝑔
The velocity of flow at any section of the duct with a cross-sectional area of is determined as:
𝑣 =
𝑄
𝐴
Procedure of the Experiment (fluid flow rate)
1. Plugin the device to the electricity power and turn on the pump.
2. Bring a stopwatch and set it to zero.
3. Close the valve at the bottom of the volumetric tank, and as liquid starts flowing into the volumetric
tank start the stopwatch from 2 liters and wait until the liquid reaches a value of 5 liters.
4. After the liquid reached a value of 5 liters stop the watch.
5. Read off and note the measurement time and the high value of water in tank.
Procedure of the Experiment (Bernoulli’s Theorem Demonstration)
1. Arrange the experimentation set-up on the Hydraulic Bench such that the discharge routes the water
into the channel.
2. Make hose connection between Hydraulic Bench and unit.
3. Open discharge of Hydraulic Bench
4. Set cap nut [1] of probe compression gland such that slight resistance is felt on moving probe.
5. Open inlet and outlet ball cock.
6. Switch on pump and slowly open main cock of Hydraulic Bench.
7. Open vent valves [3] on water pressure gauges.
8. Carefully close outlet cock until pressure gauges are flushed.

6. 6
9. By simultaneously setting inlet and outlet cock, regulate water level in pressure gauges such that
neither upper nor lower range limit [4,5] is overshot or undershot.
10. Record pressures at all measurement points. Then move overall pressure probe to corresponding
measurement level and note down overall pressure.
11. Determine volumetric flow rate. To do so, use stopwatch to establish time t required for raising the
level in the volumetric tank of the Hydraulic Bench.
Calculation of (fluid flow rate)
Table of reading (fluid flow rate)
NO. V (liter) t (s)
1 0 0
2 3 27.04
3 3 16.11
4 4 17.30
5 8 22.06
Sample of calculation:
- Convert the liter to cubic meter by multiplying the liter unit with 0.001
- The volume flow rate can be shown as: 𝑄 =
𝑉
𝑡
which can be in (
𝑚3
𝑠
) 𝑜𝑟 (
𝐿
𝑠
)
- The mass flow rate can be shown as: ṁ = 𝜌𝑄 which can be in (
𝐾𝑔
𝑠
) (1000*Q)
- The weight flow rate can be shown as: ẇ = 𝜌𝑔𝑄 which can be in (
𝑁
𝑠
) (1000*9.81*Q)
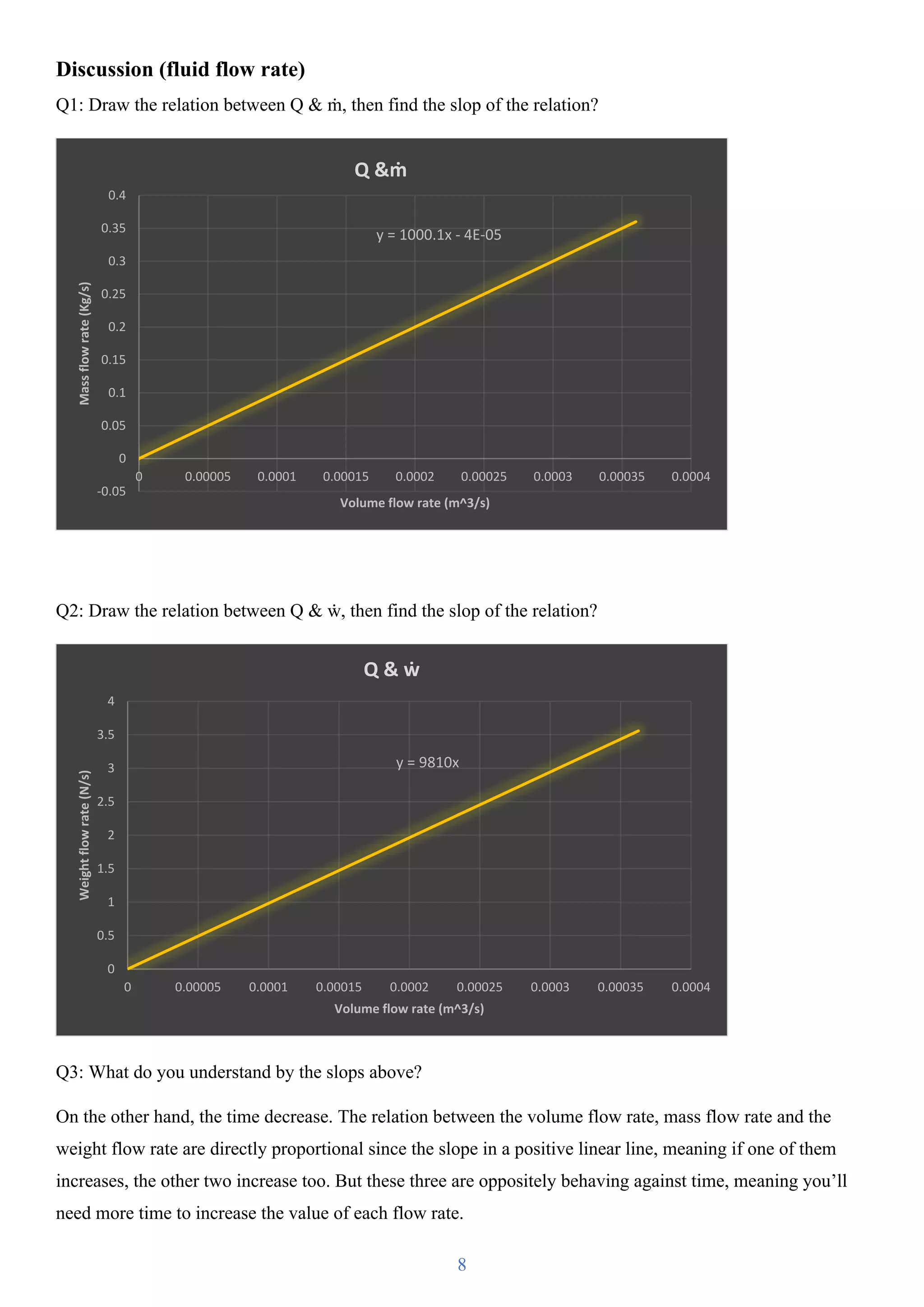
Table of calculation (fluid flow rate)
NO. V (m^3) t (s) Q (
𝒎𝟑
𝒔
) ṁ (
𝑲𝒈
𝒔
) ẇ (
𝑵
𝒔
)
1 0 0 0 0 0
2 0.003 27.04 0.000111 0.110946746 1.088387574
3 0.003 16.11 0.00018622 0.186219739 1.826815642
4 0.004 17.30 0.000231214 0.231213873 2.268208092
5 0.008 22.06 0.000362647 0.362647325 3.557570263

7. 7
Calculation of Bernoulli’s Theorem Demonstration
Table of readings (Bernoulli’s Theorem Demonstration)
NO. Hpez =
𝑷
𝝆𝒈
+ 𝒛 (cm) Hm (cm) V
(liter)
t (s)
Hp1 Hp2 Hp3 Hp4 Hp5 Hp6 Hm1 Hm2 Hm3 Hm4 Hm5 Hm6
1 16 15 0 7 12 13 19.7 19.5 18.4 17 16.5 15.7 4 12.12
2
3
4
5
Sample of calculation:
𝑄 = 𝑣𝐴 → 𝑣 =
𝑄
𝐴
(
𝑐𝑚
𝑠
)
d1=2.84cm, d2=2.25cm, d3=1.4cm, d4=1.72cm, d5=2.42cm, d6=2.84cm
ℎ𝑑 =
𝑣2
2𝑔
𝐻𝑐𝑎𝑙𝑐𝑢𝑙𝑎𝑡𝑒𝑑 =
𝑃
𝛾
+=
𝑣2
2𝑔
+ 𝑍 = ℎ𝑑 + 𝐻𝑠
Table of Calculation (Bernoulli’s Theorem Demonstration)
N
O.
Q Hs =
𝑷𝒔
𝝆𝒈
(cm) Hd (cm)
Hs1 Hs2 Hs3 Hs4 Hs5 Hs6 Hd1 Hd2 Hd3 Hd4 Hd5 Hd6
1 0.00033 16 15 0 7 12 13 1.33 3.38 22.56 9.9 2.527 1.33
1 Q H calculated (cm) Hm (cm)
0.00033 Hcal1 Hcal2 Hcal3 Hcal4 Hcal5 Hcal6 Hm1 Hm2 Hm3 Hm4 Hm5 Hm6
17.33 18.38 22.56 16.9 14.527 14.33 19.7 19.5 18.4 17 16.5 15.7

8. 8
Discussion (fluid flow rate)
Q1: Draw the relation between Q & ṁ, then find the slop of the relation?
Q2: Draw the relation between Q & ẇ, then find the slop of the relation?
Q3: What do you understand by the slops above?
On the other hand, the time decrease. The relation between the volume flow rate, mass flow rate and the
weight flow rate are directly proportional since the slope in a positive linear line, meaning if one of them
increases, the other two increase too. But these three are oppositely behaving against time, meaning you’ll
need more time to increase the value of each flow rate.
y = 1000.1x - 4E-05
-0.05
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0 0.00005 0.0001 0.00015 0.0002 0.00025 0.0003 0.00035 0.0004
Mass
flow
rate
(Kg/s)
Volume flow rate (m^3/s)
Q &ṁ
y = 9810x
0
0.5
1
1.5
2
2.5
3
3.5
4
0 0.00005 0.0001 0.00015 0.0002 0.00025 0.0003 0.00035 0.0004
Weight
flow
rate
(N/s)
Volume flow rate (m^3/s)
Q & ẇ

9. 9
Discussion (Bernoulli’s Theorem Demonstration)
Q1: Plot the pressure head (
ps
γ
) along the venture tube.
Q2: Plot the velocity head (
v2
2g
) along the venture tube.
0
2
4
6
8
10
12
14
16
18
0 1 2 3 4 5 6 7
head
pressure
Venturi
head pressure
0
5
10
15
20
25
0 1 2 3 4 5 6 7
Velocity
head
Venturi
velocity head

10. 10
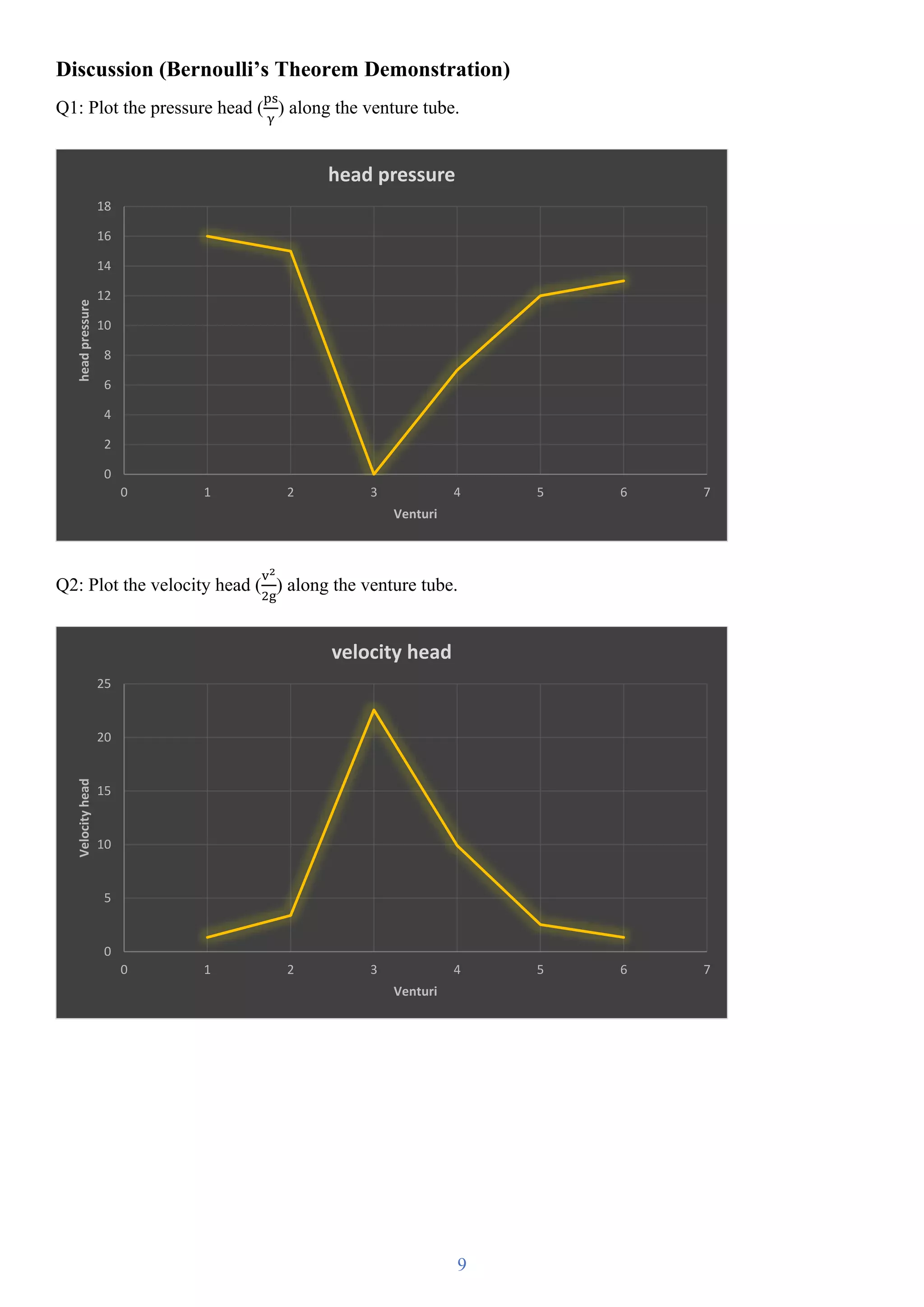
Q3: Plot the total energy H calculated and Hm along the venture tube.
Q4: Discuss the relations above.
- Values of the Hm and H calculated from the venturi are nearly
equal to each other proving the correction of the Bernoulli
equation by inputting Z=0 because the venturi is horizontal.
- The pressure head at the 3rd
point has decreased too much that we
couldn’t even read it on the tubes, but can see the water level and assume it with zero. And notice
that as the pressure has decreased, the velocity is at its maximum value.
References
1. Armfield. 2021. F1-15 Bernoulli's Theorem Demonstration - Armfield. [online] Available at:
<https://armfield.co.uk/product/f1-15-bernoullis-theorem-demonstration/> [Accessed 16 January 2021].
2. Ahmari, H. and Kabir, S., 2021. Experiment #2: Bernoulli’S Theorem Demonstration. [online]
Uta.pressbooks.pub. Available at: <https://uta.pressbooks.pub/appliedfluidmechanics/chapter/experiment-2/>
[Accessed 16 January 2021].
3. Adamslab.co.uk. 2021. Basic Flow Experiments Bench: Hydraulics Bench And Accessories. [online] Available
at: <http://adamslab.co.uk/index.php?route=product/product&product_id=4403> [Accessed 16 January 2021].
4. Steemit.com. 2021. Hydraulic Bench Tools In Hydraulics Science As Well As Research Functions And
Processes. — Steemit. [online] Available at: <https://steemit.com/science/@aguess/hydraulic-bench-tools-in-
hydraulics-science-as-well-as-research-functions-and-
processes#:~:text=hydraulics%20bench%20are%20used%20to,with%20a%20water%20discharge%20tub.>
[Accessed 16 January 2021].
0
5
10
15
20
25
0 1 2 3 4 5 6 7
Hcalculated
&
Hm
Venture Points