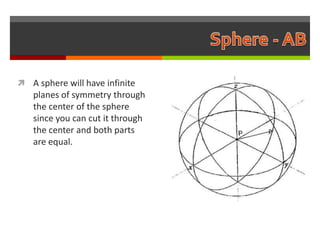
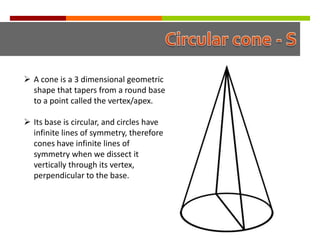
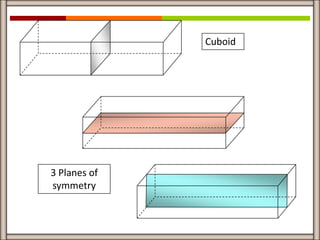
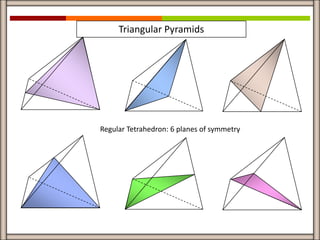
This document discusses an MYP assessment completed by a group on the topic of planes of symmetry of 3D objects. The group's guiding question asks how one's reflection in the mirror relates to their true self. The document then provides examples and descriptions of different 3D shapes and their various planes of symmetry, including cubes, cuboids, pyramids, spheres, cones, and cylinders. It reflects on skills learned from the assessment like problem solving, teamwork, and critical thinking.

1. 
Ajay Naik, Abhishek Shah, Saumya Baheti

2.  Our group has been given the task to analyze,
understand and present the plane of symmetry of
3D objects.
 We have to connect the information we obtain to
our guiding question.
 This task is MYP based, and will be graded on the
investigate criterion.

3.  Our Guiding Question is: How Is our Reflection in
the mirror our true selves?
 Objectively, this guiding question seems to be weak,
but when you think about it subjectively, a whole
new realm of ideas is unleashed.
 The guiding question uses our syllabus very
carefully, as a metaphor, to connect it to real life.

4.  A plane of symmetry divides a three dimensional
shape into two congruent halves that are mirror
images of each other.
 This means that if you cut a 3-D object from any
side or angle and it turns out to be congruent with
the other, its called a plane of symmetry.

5.  Symmetry seems to be such a small aspect of the study
of Geometry, however it is an integral component
connecting Mathematics to the real world.
 Symmetry can be found in everyday items, however the
connections to Mathematics are rarely noted.
 Symmetry, in the real world, is expressed in many pieces
of art, for example, quilts are highly mathematical in
their creation, and depict how symmetry and
mathematics are linked to real-life uses.
 Symmetry aids students in learning how to classify
objects according to the arrangement of their
constituent parts.

6.  Ordering and classification are skills that are used throughout
many daily tasks, and the ability to notice patterns or
similarities will make these tasks much easier to carry out.
 The study of symmetry in schools should look beyond
geometric forms to organic shapes, meaning animals, plants,
and everyday items.
 Children learn concepts about geometric shapes at a very
early age. They learn, first, about a shape as a whole, but,
with the help of symmetry, children learn how to focus on the
characteristics and parts of an object.
 The teaching of symmetry holds great importance in the
development of mathematical minds of students as it gives
students a different perspective of the world around them.

7.  It has six flat sides, each of which is a square of the same size,
with three meeting at each vertex.
 All edges are equal and any two intersection edges form right
angles.
 A cube is also a prism, because it is a square throughout its
length.
 It is also called a regular hexahedron.

9.  It has six flat sides and all angles are right angles.
 And all of its faces are rectangles.
 It is also a prism because it has the same cross-
section along a length.
 Its known commonly as a rectangular prism.
 Volume: Breadth x Width x Height.
 Surface Area: 2wl + 2lh + 2hw

10. Cuboid
3 Planes of
symmetry

11.  There are 6 lines of symmetry.
 The three side faces are triangles and the base
shape is a triangle.
 4 Vertices
 6 Edges
 Volume: 1/6 Height x Width x Breadth
 Surface Area: l

12.  The tetrahedron has 4 vertices, 6 edges and 4 faces,
each of which is an equilateral triangle.
 There are 6 planes of reflectional symmetry, one of
which is shown on the below. Each such plane
contains one edge and bisects the opposite edge.

13. Triangular Pyramids
Regular Tetrahedron: 6 planes of symmetry

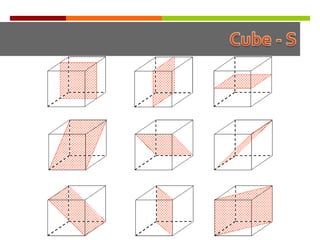
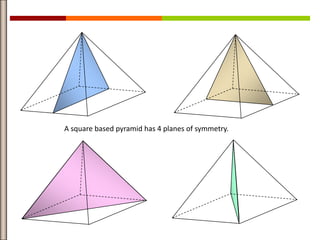
14.  A square based pyramid is a very interesting object.
 It has 4 planes of symmetry:
 The 4 Side Faces are Triangles
 The Base is a Square
 It has 5 Vertices (corner points)
 It has 8 Edges
 Surface Area = [Base Area] + 1/2 × Perimeter × [Slant Length]
 Volume = 1/3 × [Base Area] × Height

15. A square based pyramid has 4 planes of symmetry.

16.  A sphere will have infinite
planes of symmetry through
the center of the sphere
since you can cut it through
the center and both parts
are equal.

17.  A cone is a 3 dimensional geometric
shape that tapers from a round base
to a point called the vertex/apex.
 Its base is circular, and circles have
infinite lines of symmetry, therefore
cones have infinite lines of
symmetry when we dissect it
vertically through its vertex,
perpendicular to the base.

18.  Two of the faces of a
cylinder are circles.
 Circles have an infinite
number of lines of
symmetry.
 Therefore cylinders have an
infinite number of planes of
symmetry.

19. This MYP Assessment has helped me learn a lot. This assessment.
This assessment made me realize the importance of MYP, and how
helpful it is. By completing this assignment, I have gained skills in
many areas:
 Problem Solving: My friends and I overcame many problems that
arose during the process of our presentation.
 Team-Work: Whatever work we have done, and whatever
problems we have overcome, we have done it as a team.
 Critical thinking: We used critical thinking to analyze our guiding
question, and work around it.

20.  I would connect this assessment to the AOI Human Ingenuity. I
believe this Is appropriate, because this topic, and the guiding
question itself, is derived from the critical thinking skills that
humans have been rewarded with.
 I believe that working with my teammates has been a pleasure. I
truly want to commend the organizational skills, and the quick,
intuitive thinking that both my peers, Saumya, and Abhishek
clearly displayed during the course of the assignment. I look
forward to getting more opportunities to work with them in the
near future.