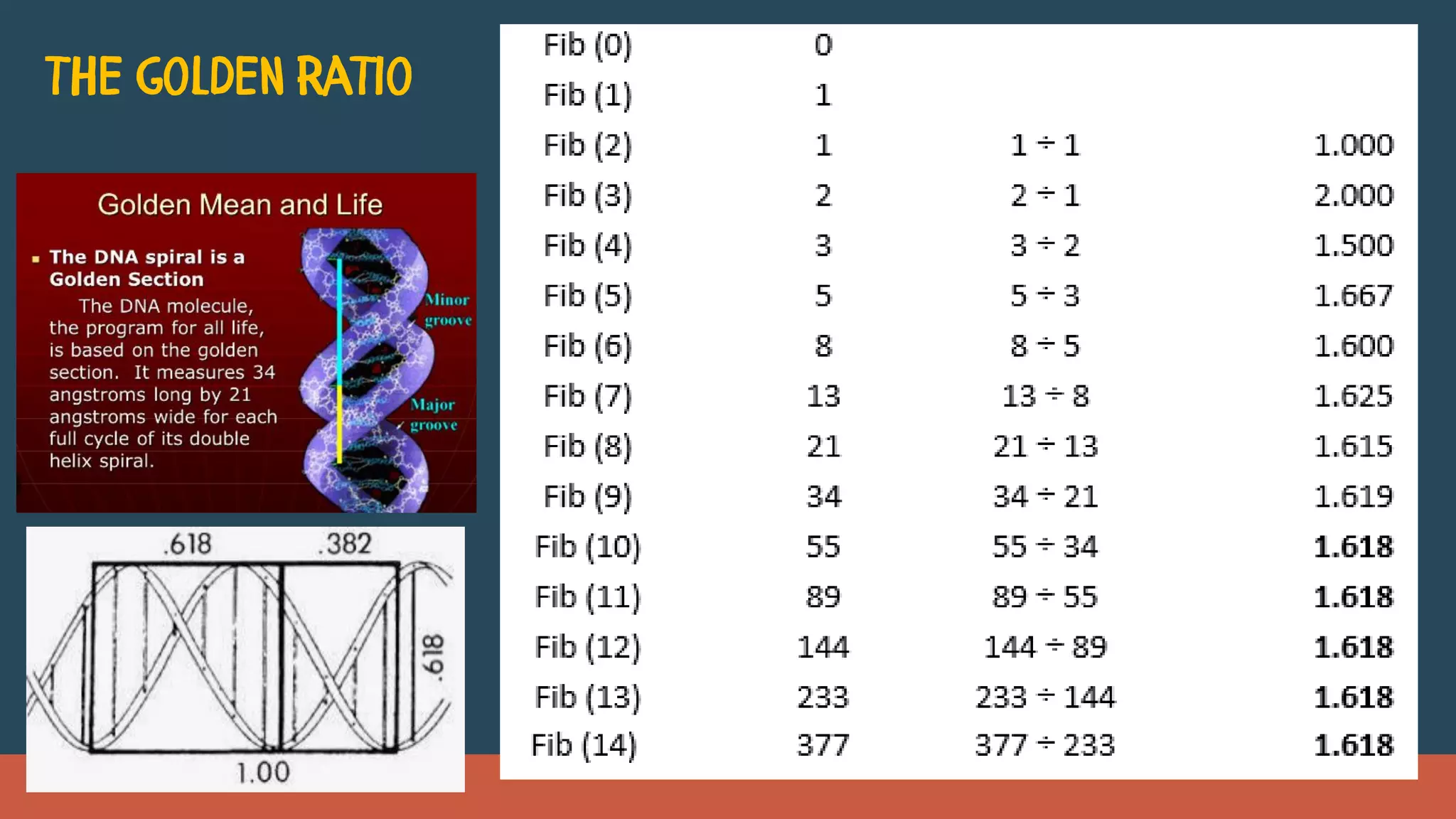
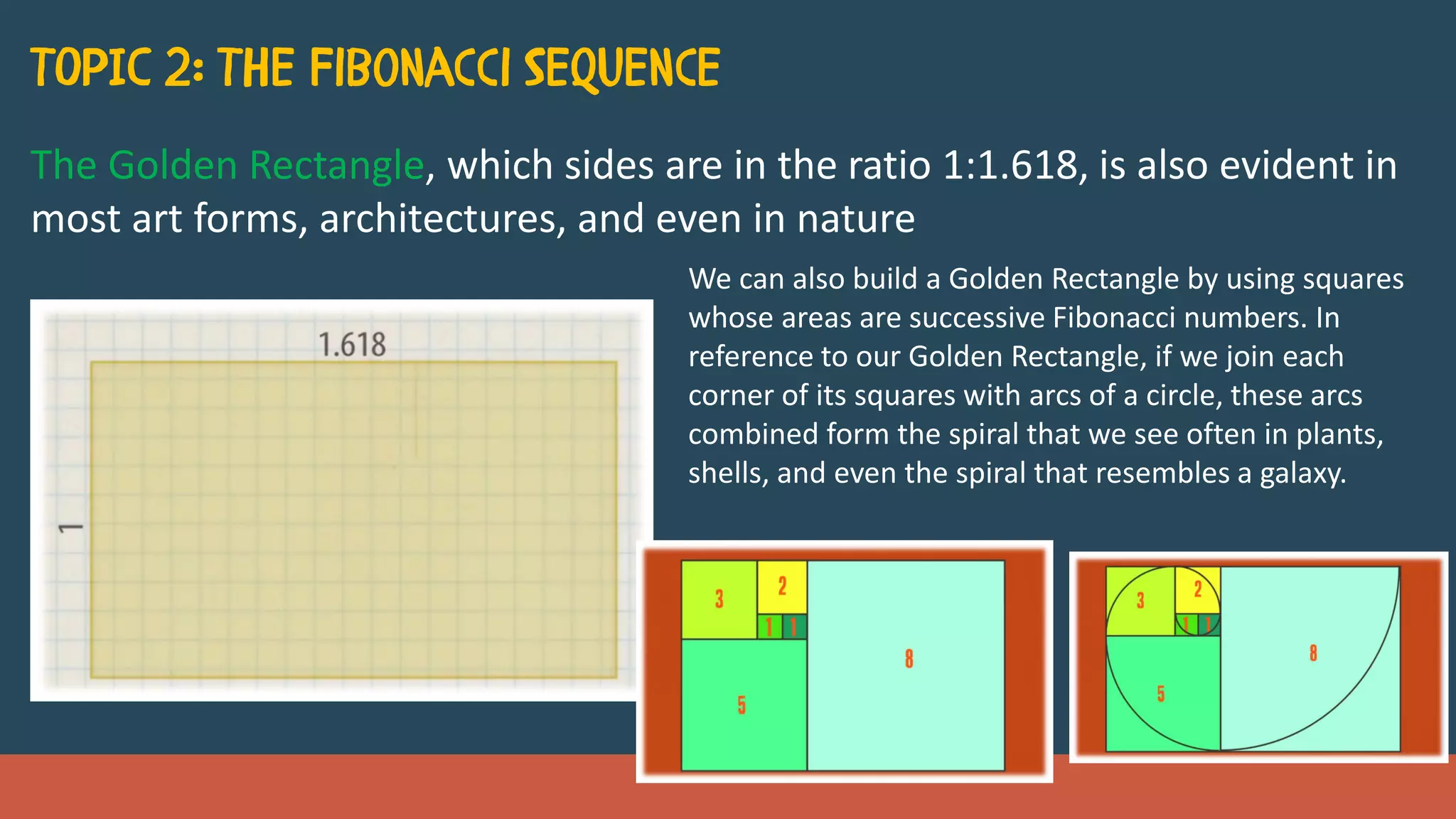
Mathematics is evident everywhere in nature and is an integral part of our lives. It is the science of patterns, quantities and relationships. The document discusses several examples of patterns in nature like geometric shapes, symmetry, the Fibonacci sequence and golden ratio that are all deeply rooted in mathematics. It also elaborates on the importance and applications of mathematics in fields like science, technology, medicine and more, establishing it as an indispensable and universal language.

2. AT THE END OF THIS LESSON,THE STUDENTS WOULD BE ABLE TO :
Identifypatternsinnatureand
regularities intheworld.
Argueaboutthenatureof
mathematics. (What itis?Howitis
expressed,represented andused?)
Articulate theimportanceof
mathematicsinone’slife.
Expressappreciationfor
mathematicsasahumanendeavor.

3. • NumbersandPatternsin
Nature&intheModernWorld
• TheFibonacciSequence

4. The laws of nature are but the mathematical
thoughts of God"
- Euclid
Euclid was an ancient Greek mathematician active as a geometer and logician. Considered the "father of
geometry"

5. The word "mathematics" (Greek: μαθηματικά)
comes from the Greek μάθημα (máthēma), which
means learning, study, science, and additionally
came to have the narrower and more technical
meaning "mathematical study",

6. The abstract science of number, quantity, and space. Mathematics may be studied in its own right ( pure
mathematics ), or as it is applied to other disciplines such as physics and engineering ( applied mathematics ).
oxford Languages
The science of numbers and their operations, interrelations, combinations, generalizations, and abstractions and
of space configurations and their structure, measurement, transformations, and generalizations Merriam-
Webster
Mathematics, the science of structure, order, and relation that has evolved from counting, measuring, and
describing the shapes of objects. Brittanica
Mathematics is the science that deals with the logic of shape, quantity and arrangement. Math is all around us, in
everything we do. Live Science
The study of the measurement, properties, and relationships of quantities and sets, using numbers and symbols.
YourDictionary

7. Mathematics is for Prediction - Applying the concepts of probability, experts can
calculate the chance of an event occurring.
Mathematics is for Organization - Social media analysts can crunch all online postings
using software to gauge the netizen’s sentiments of particular issues of personalities.
Mathematics is for Control - With the threats of climate change and global warming,
it is believed that man should change his behavior to save himself and his planet.
MATHEMATICS HELPS CONTROL NATURE AND OCCURRENCESS IN THE WORLD FOR
OUR OWN ENDS Mathematics reveals hidden patterns that help us understand the
world
Mathematics is Indispensable - Mathematics at its most basic level, logical reasoning
and critical thinking are crucial skills that are needed in any endeavor.

8. Mathematics is a useful way to think about nature and our
world. The nature of mathematics underscores the
exploration of patterns (in nature and the environment).
Mathematics is an integral part of daily life ; formal or
informal. It is used in technology, business, medicine,
natural and data sciences, machine learning and
construction. Mathematics has numerous applications in
the world making it indispensable

9. It is safe to say the mathematics is the science and art of
numbers, patterns, and relationships. Anywhere you look,
you will see measurements, patterns, and relationships.
Mathematics is evident in nature, in man-made arts,
designs in architectures, used as a language by any science
and even in the cyberspace or virtual worlds. Thus,
mathematics is everywhere.

10. In this fast-paced society, how often have you stopped to
appreciate the beauty of the things around you?
As human beings we tend to identify and follow patterns
whether consciously or subconsciously.
Early humans recognized the repeating interval of day and
night, the cycle of the moon, the rising and falling of tides
and the changing of seasons. Awareness of these patterns
allowed humans to survived.

11. Mathematics is all around us. As we discover more and
more about our environment and our surroundings we see
that nature can be described mathematically. The beauty of
a flower, the majesty of a tree, even the rocks upon which
we walk can exhibit natures sense of symmetry.
Although there are other examples to be found in
crystallography or even at a microscopic level of nature.

12. In the general sense of the word patterns are regular,
repeated or recurring forms or designs. We see patterns
everyday such as 2, 4, 6, 8 these are number patterns. The
most basic pattern is the sequence of the dates in the
calendar.

13. • Geometrical Shapes
• Symmetry
• Fibonacci spiral
• The golden ratio
• Fractals
• Stripes

14. Shapes - Perfect
Earth is the perfect shape for minimizing the pull of gravity
on its outer edges - a sphere (although centrifugal force
from its spin actually makes it an oblate spheroid, flattened
at top and bottom). Geometry is the branch of math's that
describes such shapes.

15. Shapes - Polyhedra
For a beehive, being close is important to maximise the use of
space. Hexagons fit most closely together without any gaps; so
hexagonal wax cells are what bees create to store their eggs
and larvae. Hexagons are six-sided polygons, closed, 2-
dimensional, many-sided figures with straightedges.

16. Shapes - Cones
Volcanoes form cones, the steepness and height of which
depends on the runniness (viscosity) of the lava. Fast, runny
lava forms flatter cones; thick, viscous lava forms steep-
sided cones. Cones are 3-dimensional solids whose volume
can be calculated by 1/3 x area of base x height

17. Shapes - Parallel lines
In mathematics, parallel lines stretch to infinity, neither converging
nor diverging. These parallel dunes in the Australian desert aren't
perfect - the physical world rarely is.

18. Symmetry is everywhere. Symmetry is when a figure has
two sides that are mirror images of one another. It would
then be possible to draw a line through a picture of the
object and along either side the image would look exactly
the same. This line would be called a line of symmetry.
There are two kinds of Symmetries
• Bilateral symmetry
• Radial symmetry

19. • One is Bilateral Symmetry in which an object has two
sides that are mirror images of each other.
• The human body would be an excellent example of a
living being that has Bilateral Symmetry.

20. The other kind of symmetry is Radial Symmetry. This is where there is a center point and
numerous lines of symmetry could be drawn. Radial symmetry is rotational symmetry
around a fixed point known as the center. Radial symmetry can be classified as either cyclic
or dihedral. Cyclic symmetries are represented with the notation Cn, where n is the number
of rotations. Each rotation will have an angle of 360/n. For example, an object having C3
symmetry would have three rotations of 120 degrees. Dihedral symmetries differ from
cyclic ones in that they have reflection symmetries in addition to rotational symmetry.
Dihedral symmetries are represented with the notation Dn where n represents the number
of rotations ,as well as the number of reflection mirrors present. Each rotation angle will be
equal to 360/n degrees and the angle between each mirror will be 180/n degrees. An
object with D4 symmetry would have four rotations, each of 90 degrees, and four reflection
mirrors, with each angle

22. A starfish provides us with a Dihedral 5
symmetry. Not only do we have five
rotations of 72 degrees each, but we also
have five lines of reflection.

23. Hibiscus - C5 symmetry. The petals
overlap, so the symmetry might not be
readily seen. It will be upon closer
examination though

24. A fractal is a never-ending pattern. Fractals are infinitely
complex patterns that are self-similar across different
scales. They are created by repeating a simple process over
and over in an ongoing feedback loop. Driven by recursion,
fractals are images of dynamic systems – the pictures of
Chaos.

26. These numbers are natures numbering system. They appear
everywhere in nature, from the leaf arrangement in plants, to the
pattern of florets of a flower, the bracts of a pinecone or the scales of a
pineapple. The Fibonacci numbers are therefore applicable to the
growth of every living thing including a single cell, a grain of wheat, a
hive of bees and even all mankind
A sequence refers to an ordered list of numbers called terms, that may
have repeated values, and the arrangement of these terms is set by a
definitive rule.

27. For instance, if we look at flowers, we will see that there are flowers
with numbers of petals such as three, five, eight, and so on.

28. Fibonacci Sequence is a number sequence
developed by a 13th century mathematician
known as Leonardo of Pisa (a.k.a. Fibonacci). The
Fibonacci sequence is an ordered list of numbers
that is formed by adding the preceding two
numbers and it begins with 0, 1, and 1, Then keep
adding the previous two numbers to get the next
one in which case 1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5;
and so on. It gives us the following numbers:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …

29. Fibonacci numbers
If you construct a series of squares with lengths equal to the Fibonacci
numbers (1,1,2,3,5, etc) and trace a line through the diagonals of each
square, it forms a Fibonacci spiral. Many examples of the Fibonacci spiral can
be seenin nature,including in the chambers ofa nautilusshell.

31. The golden ratio, also known as the golden number, golden proportion, or
the divine proportion, is a ratio between two numbers that equals
approximately 1.618. Usually written as the Greek letter phi, it is strongly
associated with the Fibonacci sequence, a series of numbers wherein each
number is added to the last.
If examined further, the relationship or the ratio of one Fibonacci number to
another as it progresses, is bound to arrive at a value discovered by the
Greeks even way before Fibonacci: Phi (fie) and also known called as The
Golden Ratio.

33. The Golden Ratio or 1.618 is
considered to be the aesthetically
pleasing proportion. In fact the
number was used by a famous
Greek sculptor named Phidias. He
proportioned his art with
approximate linear ratio (The
Golden Ratio) of 1:1.618 to
illustrate the idea of physical
perfection

34. The Golden Rectangle, which sides are in the ratio 1:1.618, is also evident in
most art forms, architectures, and even in nature
We can also build a Golden Rectangle by using squares
whose areas are successive Fibonacci numbers. In
reference to our Golden Rectangle, if we join each
corner of its squares with arcs of a circle, these arcs
combined form the spiral that we see often in plants,
shells, and even the spiral that resembles a galaxy.

35. The girl with the pearl earing
By Johannes Vermeer
The Monalisa by Leonardo da Vinci

36. The more we look in to natural
phenomena - the more we see the
evidences of the Golden Ratio and the
Golden Angles and it often leads us to
spirals.

37. Mathematics is everywhere in this universe. We seldom
note it. We enjoy nature and are not interested in going
deep about what mathematical idea is in it. mathematics
express itself everywhere, in all most every facet of life- in
nature all around us.

38. THANK YOU
SUGGESTED LEARNING RESOURCES:
Main Reference/ Core Textbook - Mathematics in The Modern World by Aufmann, et al.
Nature’s Numbers by Ian Stewart
Nature by Numbers https://vimeo.com/9953368
One Mathematical Cat, Please! http://www.onemathematicalcat.org/cat_book.htm
Cryptarithms Online http://cryptarithms.awardspace.us/
Math in our world by Sobecki, Bluman & Schirck- Matthew
University of Utah (2013). “Suplemental Notes Math 1090 - 008”. Department of Mathematics. Retrieved
from http://www.math.utah.edu/~fehr/math1090/5.2notes.pdf
FROM OMSC REMOTEXS LIBRARY
Finding Fibonacci : the quest to rediscover the forgotten mathematical genius who changed the world by
Devlin, Keith 2017
Mathematics: Foundations of Mathematics by Giuseppina Ronzitti 2009
Mathematics Learning by Mitchell J. Nathan, Alan H. Schoenfeld, Vera Kemeny, Susanne P. Lajoie, Nancy c.
Lavigne and Michael t. Battista 2002
Statistics by K. Lee Lerner and Brenda Wilmoth Lerner 2006
Basic statistics by Thomas, Seemon 2014
K. Lee Lerner and Brenda Wilmoth Lerner 2013