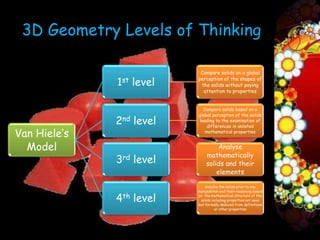
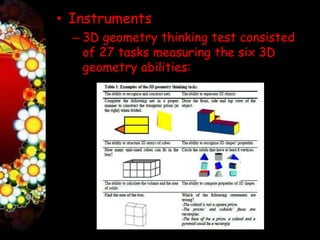
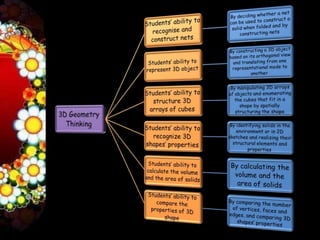
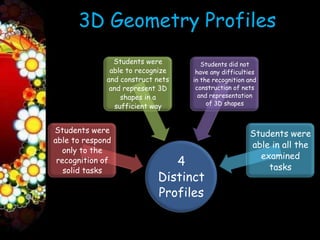
The document summarizes two papers on students' understanding of 3D geometry. The first paper examined students' 3D geometry thinking profiles and identified four distinct profiles based on their performance on tasks involving representing, constructing nets, and analyzing properties of 3D shapes. The second paper investigated differences between students' visualizations, verbal descriptions, and drawings of 3D shapes. It found students often focused on non-mathematical aspects and properties in their responses, and drawings did not always match their visualizations. There were improvements with grade level but still inconsistencies across representations.

1. PS 4227
C & T: Mathematics III
Critical Review
1. Students’ 3D Geometry 2. Students’ Visualisations
Thinking Profile of 3D Shapes
Presented by:
08B0510 SUHANA BINTI HAMDAN

2. “Students’ 3D Geometry
Thinking Profiles”

3. INTRODUCTION
• Proceedings of the sixth Congress of the
European Society for Research in
Mathematics Education (CERME 6)
• Focuses on the constructions, description
and testing of a theoretical model for the
structure of 3D geometry thinking
• Tested the validity and applicability of the
model in Cyprus

4. PURPOSE OF THE RESEARCH
1) Examine the structure of 3D
geometry abilities by validating a
theoretical model assuming that
3D geometry thinking consists of
the 3D geometry abilities
2) Describe students’ 3D geometry
thinking profiles by tracing a
developmental trend between
categories of students

5. SUMMARY
3D Geometry
Abilities
Theoretical
Considerations 3D Geometry
Levels of
Thinking

6. 3D Geometry Abilities
1. The ability to represent 3D
objects
2. The ability to recognise and
construct nets
3. The ability to structure 3D arrays
of cubes
4. The ability to recognise 3D
shapes’ properties and compare
3D shapes
5. Calculate the volume and the area
of solids

7. 3D Geometry Levels of Thinking
Compare solids on a global
1st level perception of the shapes of
the solids without paying
attention to properties
Compare solids based on a
global perception of the solids
2nd level leading to the examination of
differences in isolated
Van Hiele’s mathematical properties
Model Analyse
mathematically
3rd level solids and their
elements
Anaylse the solids prior to any
manipulation and their reasoning based
4th level on the mathematical structure of the
solids including properties not seen
but formally deduced from definitions
or other properties

8. METHODOLOGY
• Sample
– 269 students
– From 2 primary schools and 2
secondary schools
Grade No. of students
5th 55
6th 61
7th 58
8th 63
9th 42

9. • Instruments
– 3D geometry thinking test consisted
of 27 tasks measuring the six 3D
geometry abilities:

11. RESULTS
• The results are based on:
1) 3D Geometry Thinking
2) 3D Geometry Profile

12. 3D Geometry Thinking

13. 3D Geometry Thinking
Profile

14. EVALUATION
• Format of the paper
– Language
– Organization of texts
• Findings
– Structure of 3D geometry thinking
– Students’ 3D geometry thinking
profile

16. 3D Geometry Profiles
Students were Students did not
able to recognize have any difficulties
and construct nets in the recognition and
and represent 3D construction of nets
shapes in a and representation
sufficient way of 3D shapes
Students were Students were
able to respond
able in all the
only to the
examined
recognition of 4 tasks
solid tasks
Distinct
Profiles

17. CONCLUSION
3D geometry thinking implies a large
variety of 3D geometry tasks
Six 3D geometry abilities are strongly
interrelated
The identification of students’ 3D
geometry thinking profiles extended
the literature in a way that those 4
categories of students may represent
4 developmental levels of thinking in
3D geometry

18. “Students’ Visualisations
of 3D Shapes”

19. INTRODUCTION
• Proceedings of the twenty-third
Mathematics Education Research Group of
Australasia (MERGA23)1
• Report the investigation of students’
visualisations and representations of 3D
shapes
• Describes how students focused on critical
and non-critical aspects of 3D for shapes
and whether any differences exist
between students’ visual images, verbal
descriptions and drawn representations

20. AIMS
1. How well do students visualise 3D
objects?
2. In their visualisations, do students
focus on critical or non-critical
aspects of 3D objects? Are these
aspects mathematical properties?
3. What are the differences, if any,
between students’ visual images,
verbal descriptions and drawn
representations of 3D objects?

21. SUMMARY
• Research on Students’ visualisation
abilities
– Students who differed in spatial
visualisation skills did not differ in their
ability to find correct problem
solutions, but they concluded that an
emphasis on spatial visualisation skills will
improve mathematics learning (Fennema &
Tartre, 1985)
– While visual imagery did assist many
students in solving problems, visualisers
could experience some disadvantages
(Presmeg, 1986)

22. – Visual imagery, when properly
developed, can make a substantial
contribution at all levels of geometric
thinking (Battista & Clements, 1991)
– Visual imagery was important in young
students’ noticing features of shapes
and in deciding how shapes could be
used (Owens, 1994)

23. • Theories on the Development of
Spatial Concepts
– One of the most striking things about
objects in images is how they mimic
properties of real objects
(Kosslyn, 1983)

24. – The ability to draw correct diagrams
stems from images that students
possess and often these images do not
reflect student understandings in terms
of the properties of a given figure (Pegg
& Davey, 1989)
– Students with poor visual skills may
focus on non-mathematical aspects of
shapes and this may inhibit effective
learning of geometric ideas (Gray, Pitta,
and Tall, 1997)

25. METHODOLOGY
• Sample
– 30 students
– From a NSW Department of
Education and Training school
Year No. of students
1 10 students
3 9 students
5 11 students

26. • Instrument
– Interviewed based assessment of
students’ understanding and
visualisations of 3D shapes included 8
tasks
• Adapted from instruments used in prior
studies by Battista & Clements (1996),
Shaughnessy (1999) in correspondence
• The task also reflected sample activities
from the NSW Mathematics K-6 syllabus
(NSW Department of Education, 1989)
• Were administrated on a one-one basis by
chief investigator

27. Assessment Tasks
Task 1: Visualise a three-dimensional shapes
I want you to think about a cereal box, for example, a cornflakes or rice bubbles box. Tell me all you can
think about this box.
Task 2: Identify similar shapes
Can you think of any other things or shapes in the real world that are the same shape as this cereal box
shape? Why are they the same?
Task 3: Name the mathematical shape visualised
Do you know the mathematical name of this cereal box shape?
Task 4: Draw the visualised shape
Can you draw this cereal box shape for me? Can you explain your drawing to me?
Task 5: Describe a (held) shape
I’ve got a real cereal box here. You can pick it up and turn it around if you want to. Now can you describe
the shape of this box to me? (If the description was quite different from the original visualization, the
investigator said, “You said 4 sides before, and how you have told me there are 6 sides. Why did you say
4 sides before? How was the picture in your mind different from the real box?”)
Task 6: Identify shapes needed to make up into three-dimensional shape
Here are some cardboard shapes. If you wanted to stick some of these shapes together to make one
cereal box, which shapes would you need? Hand them to me.
Task 7: Identify net of a shape
This is the shape of a cornflakes’ box flattened out. Now if you cut out these shapes (paper with nets A-
E was shown) and folded them up along the dotted lines, which ones could you make into a small cornflakes
box shape?
Task 8: describe a blank (held) shape
Now look at this box (child was shown a muesli bar box which had been folded inside out so that all faces
appear blank to avoid distraction. The student was allowed to handle the box for a few seconds. Then it
was taken from view). Now describe the shape of the box.

28. – Responses & Solution methods
• Responses were recorded on an audiotape
and students’ drawings and explanations
were retained for later analysis
• Solutions methods were coded for
correct, incorrect, or non-response
before being analysed for key
mathematical aspects
• Coding of responses was supervised and
recoded by an independent coder

29. RESULTS
• Interview transcript were anaylsed
and responses classified according
to:
1. Student performance
2. The mathematical or non-
mathematical aspects of the
responses
3. Differences between
drawn, visualised and verbal
descriptions

30. Percentage of Students’ Responses by
Category and Year Level for Tasks 1-8
Year 1 n = 12 Year 3 n = 11 Year 5 n = 11
TASK 1: visualize three-dimensional shape
Described shape using non-math props only 17% 0% 0%
Described shape using non-math and math props 83% 80% 73%
Described shape using math props only 0% 20% 27%
Unable to name any math props correctly 92% 60% 9%
Name one prop correctly 8% 30% 27%
Name two props correctly 0% 10% 55%
Name three props correctly 0% 0% 9%
Made incorrect estimate of either faces, corners or edges 50% 70% 36%
TASK 2: identify other things with the same shape
Unable to name anything with similar shape 33% 30% 18%
Named one other thing with the same shape 58% 40% 45%
Named more than one thing with the same shape 8% 30% 36%
TASK 3: name the mathematical shape visualised
Gave correct math name for shape 0% 20% 36%
TASK 4: draw visualised shape
Drew shape as 3D drawing 80% 30% 9%
Drew shape as poor 3D drawing 20% 45% 36%
Drew shape as a good 3D drawing 0% 25% 27%
TASK 5: describe a held shape
Described shape using non-math props only 17% 0% 18%
Described shape using non-math and math props 83% 90% 82%
Described shape using math props only 0% 10% 0%
Unable to name any math props correctly 75% 10% 9%
Name one prop correctly 25% 70% 55%
Name two prop correctly 0% 20% 27%
Name three prop correctly 0% 0% 9%
Made incorrect estimate of either faces, corners or edges 8% 50% 45%
TASK 6: identify shapes needed to make up into 3D shape
Chose 6 correct shapes 0% 30% 36%
Chose 6 shapes but incorrect ones 8% 20% 36%
Chose 4 shapes only 33% 30% 18%
Chose other incorrect combination of shapes 58% 20% 9%
TASK 7: identify net of shape
Identify correct nets 0% 10% 0%
TASK 8: describe “blank” held shape
Described shape using non-math props only 8% 0% 0%
Described shape using non-math and math props 92% 100% 91%
Described shape using math props only 0% 0% 9%
Unable to name any math props only 83% 30% 9%
Name one prop correctly 17% 50% 36%
Name two props correctly 0% 20% 45%
Name three props correctly 0% 0% 9%
Made incorrect estimate of either faces, corners or edges 75% 70% 67%

31. EVALUATION
• Format of the paper
– Language
– Data analysis
– Organizations of texts

32. • Findings
1. Student performance
 Students found difficulty in visualising
3D objects with an accurate awareness
of their mathematical properties
2. The mathematical or non-
mathematical aspects of the
responses
 Non-mathematical aspects featured
strongly in students’ responses across
grade levels

33. 3. Differences between drawn,
visualised and verbal descriptions
 There are considerable differences
between students’ abilities on these 3
aspects

34. CONCLUSION
 The accuracy of drawing a 3D shape
which a student has just visualised
does not necessarily reflect the
student’s visualisation ability
 The quality of some student’s
visualisations may improve with grade
level, but that students may remain
focused on non-mathematical or non-
critical aspects of shapes